[논문 요약] A Fast Learning Algorithm for Deep Belief Nets

🎈 Introduction

Directed Delief Network

Directed Belief Network는 다음과 같은 경우 학습하기 어렵다.

• 노드들이 서로 복잡하게 연결되어 있을 때
• 은닉층이 많이 있을 때

그 이유는 특정 행동이 발생하는 정확한 원인을 추론하기 어렵기 때문이다.

Variational method는 이 문제를 해결하고자 복잡한 분포를 간단하게 근사시키지만, 다음과 같은 문제점을 갖는다.

• 실제로는 독립이 아닌 깊은 층의 노드를 독립이라고 가정하면 근사가 완전히 잘못될 수 있다
• 굉장히 많은 파라미터를 사용하며 학습이 오래 걸린다

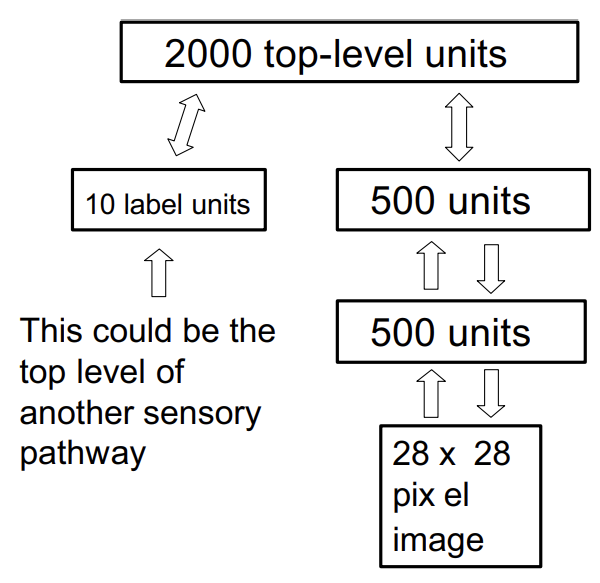
본 논문은 이 문제를 해결하기 위해 다음과 같은 구조의 네트워크를 제안한다.

이 모델은 몇 가지 매력적인 특징을 지닌다.

• 매우 깊고, 많은 파라미터를 가진 네트워크에서도 유효한 파라미터를 빠르게 찾아낼 수 있는 greedy 알고리즘이 있다.

• 비지도 학습 알고리즘이지만 지도 학습에도 적용될 수 있다.

• MNIST 숫자 데이터셋에 대해 판별 모델을 능가하는 생성 모델을 학습할 수 있는 fine-tuning 알고리즘이 있다.

• 생성 모델은 깊은 층의 분포가 갖는 의미를 쉽게 해석할 수 있도록 한다.

• 추론이 빠르면서도 정확하다.

• 학습 알고리즘이 지역적이라 가중치의 변화가 직전 노드와 직후 노드의 상태에만 의존한다.

• 의사소통이 단순해 그들의 이진 상태로만 소통한다.

🎐Complementary Priors

Explaining away 효과는 Directed belief net에서의 추론을 어렵게 만든다.

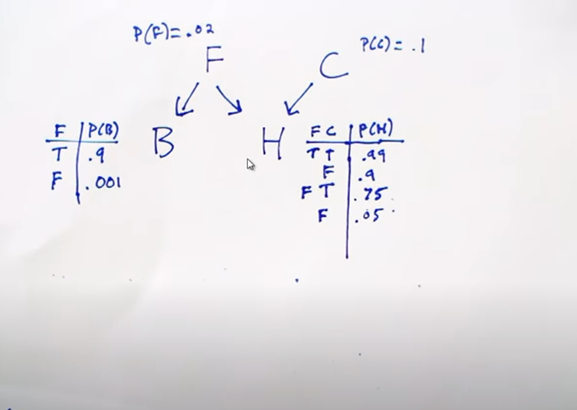
Explaining away 효과란?

   ( 영상 재생 : 이미지 클릭 )

$P(C|H)$ : 두통이 있을 때 암에 걸렸을 확률 = $0.5525$
$P(C|H,B)$ : 두통과 멍이 있을 때 암에 걸렸을 확률 = $0.112$

일어났을 때 두통이 있으면 암에 걸렸을 확률이 약 55%이다.

그런데 거울을 보고 멍이 들었음을 알게 되면 암에 걸렸을 확률이 약 11%로 감소한다.

멍이 들었다는 것은 두통이 '암'이 아니라 '싸움'이라는 또 다른 원인으로 인해 발생했을 수 있다는 사실을 설명하기 때문이다.

이와 같이 Explaining away 효과가 발생할 경우 서로 독립인 변수 '싸움'과 '암'이 서로 영향을 미치기 때문에 추론이 어려워진다.

아래에서는 Directed Belief Net에서 Explaining away 효과를 없애는 방법을 제시한다.

우선, Logistic belief net부터 알아보도록 하자.

🧶Logistic belief net

$p(s_i=1)={1\over {1+exp(-b_i-\sum_js_jw_{ij})}}$

Logistic belief net이 생성 모델로 쓰일 경우,
노드 i가 켜질 확률은 위 수식처럼 부모 노드 j의 켜짐 여부와 연결 가중치를 이용한 함수로 표현된다.

만약 logistic belief net이 하나의 은닉층만을 가진다면 은닉 노드들이 서로 독립적으로 선택되기 때문에 prior distribution이 독립 분포로 표현이 가능하다.

하지만 posterior distribution은 비독립적인데, 이는 데이터로부터의 likelihood로 인해 생긴다.

연구진은 별도의 은닉층을 추가해 이 likelihood와 완전히 정반대의 상관관계를 갖는 complementary prior를 생성함으로써 첫번째 은닉층에서 발생하는 explaining away 효과를 제거할 수 있음을 보였다.

이후 likelihood가 prior와 곱해지면 우리는 독립 분포로 표현되는 posterior를 구할 수 있다.

Complementary prior가 항상 존재한다고 확신할 수는 없지만,
다음 항목에서 소개하듯이 모든 은닉층에서 짝지어진 가중치들이 complementary prior를 생성하는 무한한 logistic belief net의 간단한 예시가 있다.

🎃 An Infinite Directed Model with Tied Weights

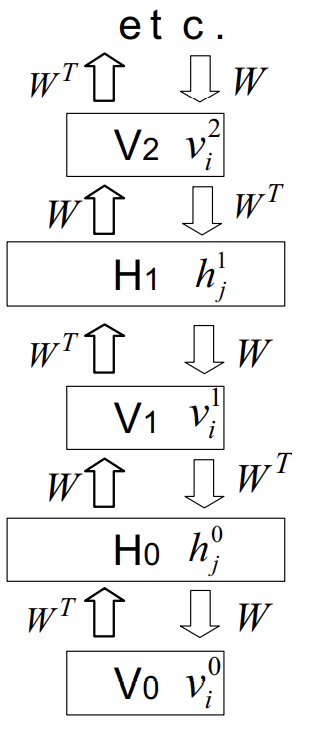
이 모델은 무한히 깊은 은닉층에서 무작위 구성으로 시작해, 활성화된 부모 노드가 베르누이 분포를 따라 특정 자식 노드를 활성화시키는 top-down 방식으로 데이터를 생성해낸다.

하지만 이 모델은 다른 방향성 네트워크와는 다르게 가시층($V_0$)의 데이터 벡터($v_i^{0}$)부터 시작해, 전치 가중치 행렬($W^{T}$)을 이용해서 각 은닉층의 독립 분포를 차례대로 유추함으로써 모든 은닉층의 실제 $posterior$를 구할 수 있다.

이제 우리는 실제 $posterior$로부터 샘플을 만들어내 그것이 데이터와 얼마나 다른지를 계산할 수 있기 때문에 데이터 $\textbf{v}^{0}$ 로그 확률의 미분값을 계산할 수 있다.

먼저 $w_{ij}^{00}$ (은닉층 $H_0$의 j 유닛과 가시층 $V_o$의 i 유닛 간의 가중치)에 대한 미분값을 구하면 다음과 같다.

${\partial\, log\,p(\textbf{v}^0)\over \partial \,w^{00}_{ij}}=<h^0_j(v_i^0-\hat{v}^0_i)>$

$<...>$는 샘플링된 값들의 평균을 뜻하며, $\hat{v_i}^{0}$는 가시 벡터 $v_i^{0}$가 샘플링된 은닉층으로부터 재생성되었을때 유닛 i가 켜져 있을 확률을 뜻한다.

만약 $\hat{v_i}^{0}$과 $v_i^{0}$가 같다면 샘플링된 은닉층으로부터 실제 가시 벡터를 완벽하게 재생성할 수 있다는 것을 뜻하며 이를 위한 방향으로 모델이 학습된다.

그런데 이때, 첫번째 은닉층 $H_0$로부터 $\hat{v_i}^{0}$을 만들어내는 것은 첫번째 은닉층 $H_0$로부터 두번째 가시층 $V_1$을 통해 두번째 은닉층 $H_1$의 사후 분포를 계산하는 것과 완벽히 동일한 과정이다.

따라서 위의 수식은 아래와 같이 바뀔 수 있다.

${\partial\, log\,p(\textbf{v}^0)\over \partial \,w^{00}_{ij}}=<h^0_j(v_i^0-v^1_i)>$

위와 같은 수식의 변화에 있어 $h_j^0$에 대한 $v_i^1$의 비독립성은 문제가 되지 않는다.

그 이유는 $v_i^0$이 $h_j^0$에 전제를 둔 확률이기 때문이다.

같은 $w_{ij}$가 여러번 중복되어 사용되기 때문에 총 미분값은 아래와 같이 모든 층 간의 가중치 미분값들의 총합으로 표현된다.

${\partial\, log\,p(\textbf{v}^0)\over \partial \,w_{ij}}=\,\,<h^0_j(v_i^0-v^1_i)>\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+<v^1_i(h_j^0-h^1_j)>\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+<h_j^1(v_i^1-v^2_i)>\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+...$

이 식을 풀어 쓰면, 가장 처음과 마지막 항을 제외하고 서로 상쇄되어 없어지고 이는 볼츠만 머신 수식과 같아진다.