그래프
vertex(정점)와 edge(간선)로 구성된 한정된 자료구조를 의미
그래프 용어
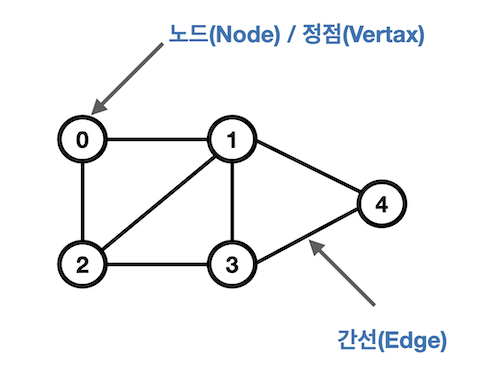
- 노드 (Node) / 정점(vertex)
→ 특정 위치 - 간선 (Edge)
→ 위치 간의 관계, 정점을 연결한 선
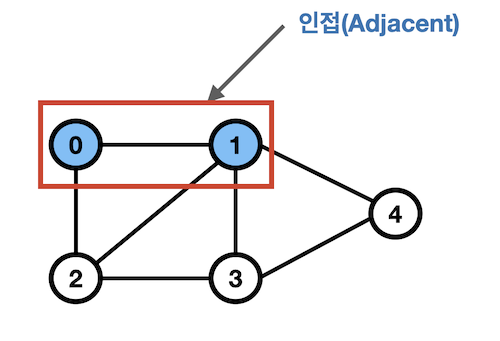
- 정점 0과 1은 간선으로 연결 → 이 때 두 노드는 인접(Adjacent)하다.
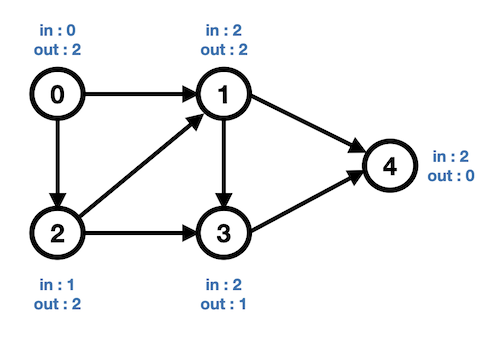
- 차수(Degree)
→ 무방향 그래프에서 하나의 정점에 인접한 정점의 수- 무방향 그래프의 차수의 합 : 그래프 간선 수 x 2
- 진입 차수(in-degree)
→ 방향 그래프에서 외부에서 오는 간선의 수 (내차수) - 진출 차수(out-degree)
→ 방향 그래프에서 외부로 향하는 간선의 수 (외차수)
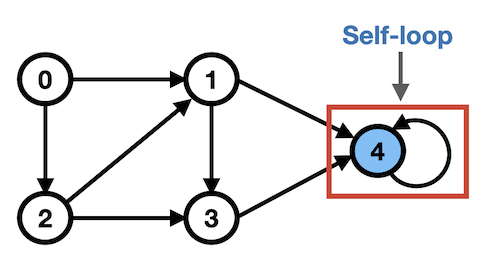
- Self-loop
→ 출발지와 목적지가 동일한 정점
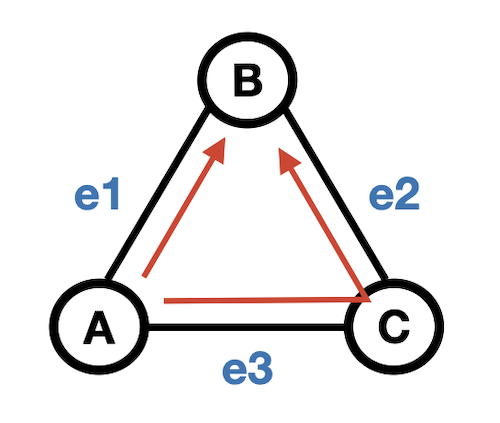
- 경로(Path)
→ 정점과 간선이 교대로 구성된 시퀀스- Path(A, B) = [A, e1, B] or [A, e3, C, e2, B]
- 단순 경로(Simple Path)
→ 정점과 간선이 중복되지 않는 경로 - 경로 길이(Path length)
→ 경로를 구성하는데 사용된 간선의 수
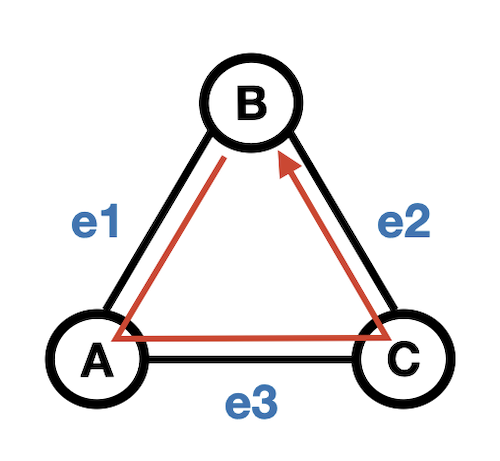
- 회로(Cycle)
→ 시작 정점과 끝 정점이 같은 경로- Cycle(B, B) = [B, e1, A, e3, C, e2, B]
그래프 종류
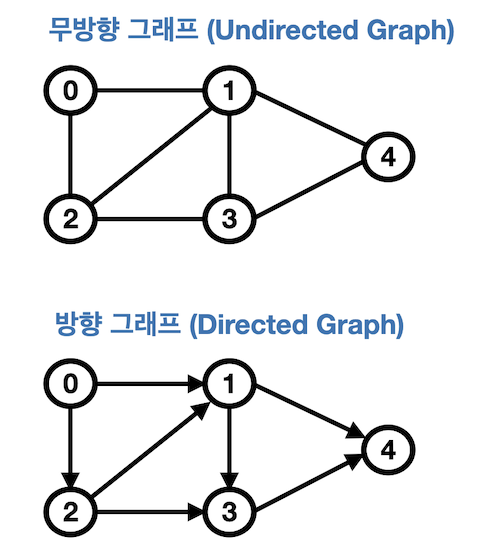
- 무방향 그래프(Undirected Graph)
→ 무향 간선으로 이루어진 그래프- 간선은 간선을 통해 양방향으로 갈 수 있다.
- 정점 0, 1을 연결하는 간선은 (0, 1) or (1, 0)으로 동일
- 방향 그래프(Directed Graph)
→ 유향 간선으로 이루어진 그래프- 0 → 1 로 가는 간선은 (0, 1)로 표현. (1, 0)과는 다름 ****
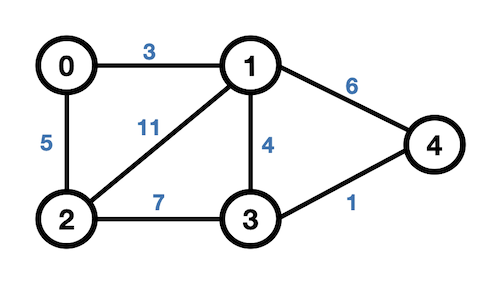
- 가중치 그래프(Weighted Graph)
→ 가중치 or 비용을 갖는 그래프- Network 라고도 한다.
- ex) 도시-도시의 연결, 도로의 길이, 톨게이트 비용 등
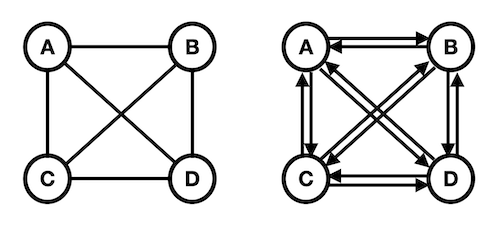
- 완전 그래프(Complete Graph)
→ 임의의 두 정점 A, B에 대해서 A, B를 잇는 간선 e(A, B)이 존재하는 그래프 - 완전 그래프는 정규 그래프(모든 정점 동일한 차수)
- N개의 정점을 가지는 무방향 그래프 → 간선의 개수 = 1/2 x N(N-1)
- N개의 정점을 가지는 방향 그래프 → 간선의 개수 = N(N-1)
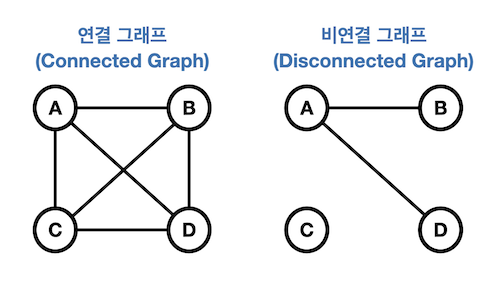
- 연결 그래프(Connected Graph)
→ 무방향 그래프에 있는 모든 정점쌍에 대해서 항상 경로가 존재하는 경우- 트리(Tree) → 사이클을 갖지 않는 연결 그래프
- 비연결 그래프(Disconnected Graph)
→ 무방향 그래프에서 특정 정점쌍 사이에 경로가 존재하지 않는 경우
그래프와 트리의 차이
| 종류 | 방향성 | 순환성 | 루트 여부 | 노드 관계 | 모델 |
|---|---|---|---|---|---|
| 그래프 | 방향 그래프 또는 무방향 그래프 | 순환 및 비순환 | 루트 노드 없음 | 부모 자식 관계 없음 | 네트워크 모델 |
| 트리 | 방향 그래프 | 비순환 | 루트 노드 존재 | 부모 자식 관계 | 계층 모델 |
그래프 표현 방법
1. 인접 행렬(Adjacency Matrix)
2차원 배열로 그래프의 연결 관계를 표현하는 방식
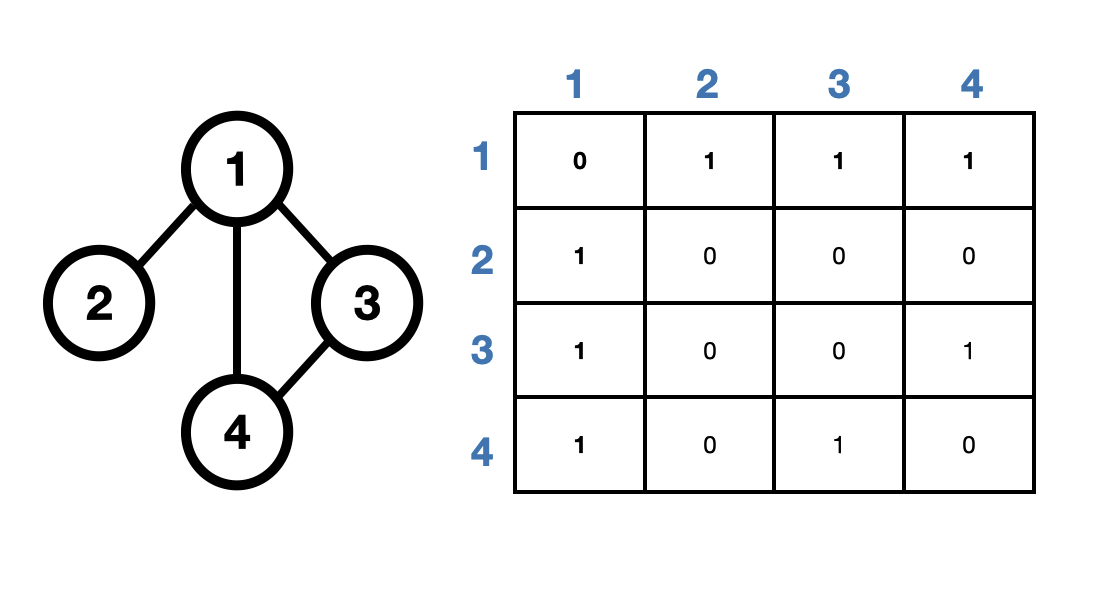
- 서로 연결이 되어있으면 1로 표시
- 서로 연결이 되어있지 않으면 0으로 표시
- 저장 공간 : O(n^2)
- 어떤 정점 v에 인접한 모든 노드 찾기 : O(n)
- 어떤 간선 (u, v)가 존재하는지 검사 : O(1)
public class AdjacencyMatrix {
public static final int INF = Integer.MAX_VALUE;
public static int[][] graph = {
{0, 7, 5},
{7, 0, INF},
{5, INF, 0}
};
public static void main(String[] args) {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
System.out.print(graph[i][j] + " ");
}
System.out.println();
}
}
}2. 인접 리스트(Adjacency List)
리스트로 그래프의 연결 관계를 표현하는 방식
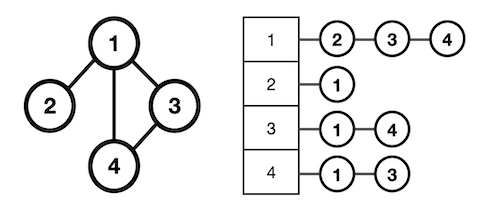
- 배열방에 모든 노드를 집어넣고, 각 배열방에 있는 해당 노드와 인접한 노드들을
Linked List로 나열해서 저장 - 저장된 노드들의 총 개수 → 2 x m(간선의 길이)
- 저장 공간 : O(n + m) / 최악의 경우 O(n^2)
- 어떤 정점 v에 인접한 모든 노드 찾기 : O(degree(v))
- 어떤 간선 (u, v)가 존재하는지 검사 : O(degree(u))
class Vertex {
private int index;
private int distance;
public Vertex(int index, int distance) {
this.index = index;
this.distance = distance;
}
public void show() {
System.out.print("(" + this.index + "," + this.distance + ") ");
}
}
public class AdjacencyList {
public static ArrayList<ArrayList<Vertex>> graph = new ArrayList<>();
public static void main(String[] args) {
for (int i = 0; i < 3; i++) {
graph.add(new ArrayList<>());
}
graph.get(0).add(new Vertex(1, 7));
graph.get(0).add(new Vertex(2, 5));
graph.get(1).add(new Vertex(0, 7));
graph.get(2).add(new Vertex(0, 5));
for (int i = 0; i < 3; i++) {
for (int j = 0; j < graph.get(i).size(); j++) {
graph.get(i).get(j).show();
}
System.out.println();
}
}
}그래프의 탐색
하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문
1. 깊이 우선 탐색 DFS (Depth-First Search)
특정한 경로를 탐색하다가 특정 상황에서 최대한 깊숙이 들어가서 노드를 방문 후,
다시 돌아가 다른 경로로 탐색하는 알고리즘
- 미로 탐색 시, 한 방향으로 갈 수 있을만큼 끝까지 가다가 더이상 길이 없으면 가장 가까운
갈림길로 돌아와 그곳부터 다른 방향으로 탐색하는 방법과 유사 - 넓게(wide)게 아닌 깊게(depth) 탐색
- 모든 노드를 방문하고자 하는 경우 이 방법 선택
깊이 우선 탐색 (DFS)의 특징
- 자기 자신을 호출하는 재귀 알고리즘 형태
- 트리의 in-, pre-, post- order 순회는 모두 DFS의 한 종류
- 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 (기존에 방문한 노드는 재방문 하지 않음.)
1-1. DFS 구현 - Stack, 재귀
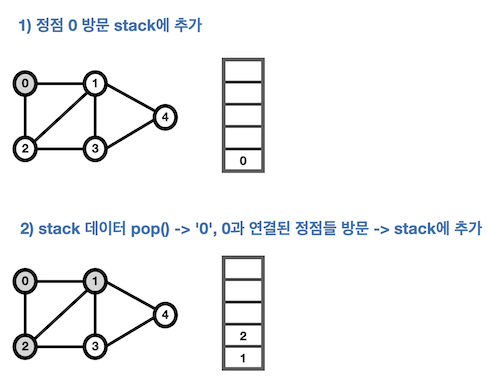
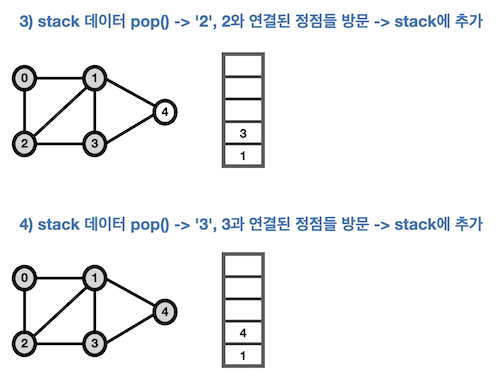
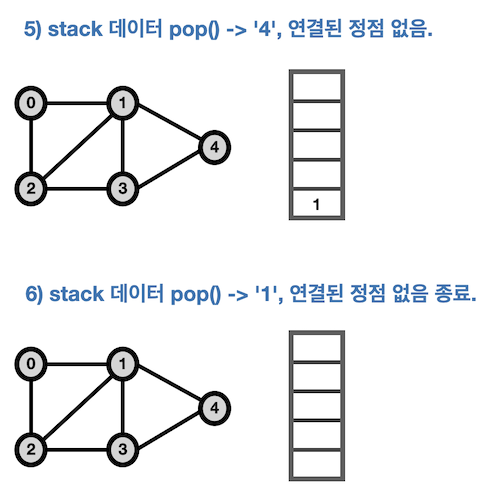
- 탐색 순서는 다음과 같다.
0 → 2 → 3 → 4 → 1
1-2. DFS 구현 - Java 코드
- 그래프 인접행렬 이용
public class GraphMatrix {
static int edge;
static int vertex;
static int[][] graph;
static boolean[] visited;
public static void main(String[] args) {
vertex = 5;
edge = 7;
graph = new int[vertex + 1][vertex + 1];
visited = new boolean[vertex + 1];
addEdge(1, 2);
addEdge(1, 3);
addEdge(2, 3);
addEdge(2, 4);
addEdge(2, 5);
addEdge(3, 4);
addEdge(4, 5);
dfs(1);
}
private static void addEdge(int i1, int i2) {
graph[i1][i2] = 1;
graph[i2][i1] = 1;
}
// 재귀
private static void dfs(int i) {
visited[i] = true;
System.out.println(i + " ");
for (int j = 1; j < vertex + 1; j++) {
if (graph[i][j] == 1 && !visited[j]) {
dfs(j);
}
}
}
}- 그래프 인접리스트 이용
class Vertex {
int data;
List<Vertex> adjacent;
boolean marked;
Vertex (int data) {
this.data = data;
this.marked = false;
adjacent = new ArrayList<>(); // or LinkedList
}
}
public class GraphList {
Vertex[] vertexes;
GraphList (int size) {
vertexes = new Vertex[size];
for (int i = 0; i < size; i++) {
vertexes[i] = new Vertex(i);
}
}
void addEdge(int i1, int i2) {
Vertex n1 = vertexes[i1];
Vertex n2 = vertexes[i2];
if (!n1.adjacent.contains(n2)) {
n1.adjacent.add(n2);
}
if (!n2.adjacent.contains(n1)){
n2.adjacent.add(n1);
}
}
void dfs() {
dfs(0);
}
// 스택
void dfs(int index) {
Vertex root = vertexes[index];
Stack<Vertex> stack = new Stack<>();
stack.push(root);
root.marked = true;
while (!stack.isEmpty()) {
Vertex r = stack.pop();
for (Vertex n : r.adjacent) {
if (!n.marked) {
n.marked = true;
stack.push(n);
}
}
visit(r);
}
}
private void dfsR(Vertex r) {
if (r == null) return;
r.marked = true;
visit(r);
for (Vertex n : r.adjacent) {
if (!n.marked)
dfsR(n);
}
}
void dfsR(int index) {
Vertex r = vertexes[index];
dfsR(r);
}
// 재귀
void dfsR() {
dfsR(0);
}
void visit(Vertex n) {
System.out.print(n.data + " ");
}
public static void main(String[] args) {
GraphList g = new GraphList(5);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(2, 3);
g.addEdge(3, 4);
g.dfs();
}
}2. 너비 우선 탐색(BFS, Breadth-First Search)
루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색
- 시작 정점에서 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법
- 깊게(depth)게 아닌 넓게(wide) 탐색
- 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 사용
너비 우선 탐색 (BFS)의 특징
- BFS는 재귀적으로 동작하지 않음
- BFS는 선입선출 방식인 큐 자료구조를 이용하는 것이 정석
- 인접한 노드를 반복적으로 큐에 넣어, 가까운 노드부터 탐색을 진행
- 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 (기존에 방문한 노드는 재방문 하지 않음.)
2-1. BFS 구현 - Queue
- 탐색 시작 노드를 큐에 삽입하고 방문 처리
- 큐에서 노드를 꺼내 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리
- 위의 과정을 더 이상 수행할 수 없을 때까지 반복
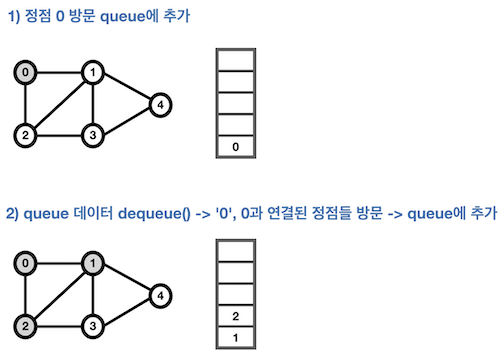
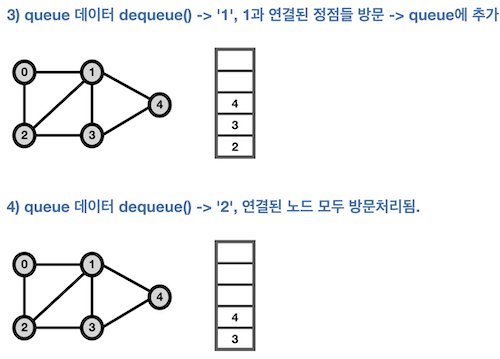
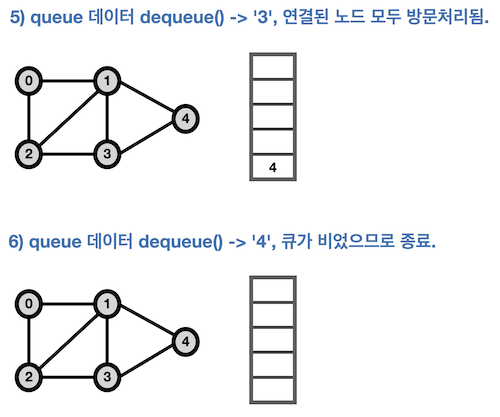
- 탐색 순서는 다음과 같다.
0 → 1 → 2 → 3 → 4
2-2. BFS 구현 - Java 코드
class Vertex {
int data;
List<Vertex> adjacent;
boolean marked;
Vertex (int data) {
this.data = data;
this.marked = false;
adjacent = new ArrayList<>(); // or LinkedList
}
}
public class GraphList {
Vertex[] vertexes;
GraphList (int size) {
vertexes = new Vertex[size];
for (int i = 0; i < size; i++) {
vertexes[i] = new Vertex(i);
}
}
void addEdge(int i1, int i2) {
Vertex n1 = vertexes[i1];
Vertex n2 = vertexes[i2];
if (!n1.adjacent.contains(n2)) {
n1.adjacent.add(n2);
}
if (!n2.adjacent.contains(n1)){
n2.adjacent.add(n1);
}
}
void visit(Vertex n) {
System.out.print(n.data + " ");
}
void bfs() {
bfs(0);
}
void bfs(int i) {
Vertex root = vertexes[i];
Queue<Vertex> queue = new LinkedList<>();
queue.add(root);
root.marked = true;
while(!queue.isEmpty()) {
Vertex r = queue.poll();
for (Vertex v : r.adjacent) {
if (!v.marked) {
v.marked = true;
queue.add(v);
}
}
visit(r);
}
}
public static void main(String[] args) {
GraphList g = new GraphList(5);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(2, 3);
g.addEdge(3, 4);
g.bfs(); // 0 1 2 3 4
}
}