
1149번 RGB거리
문제
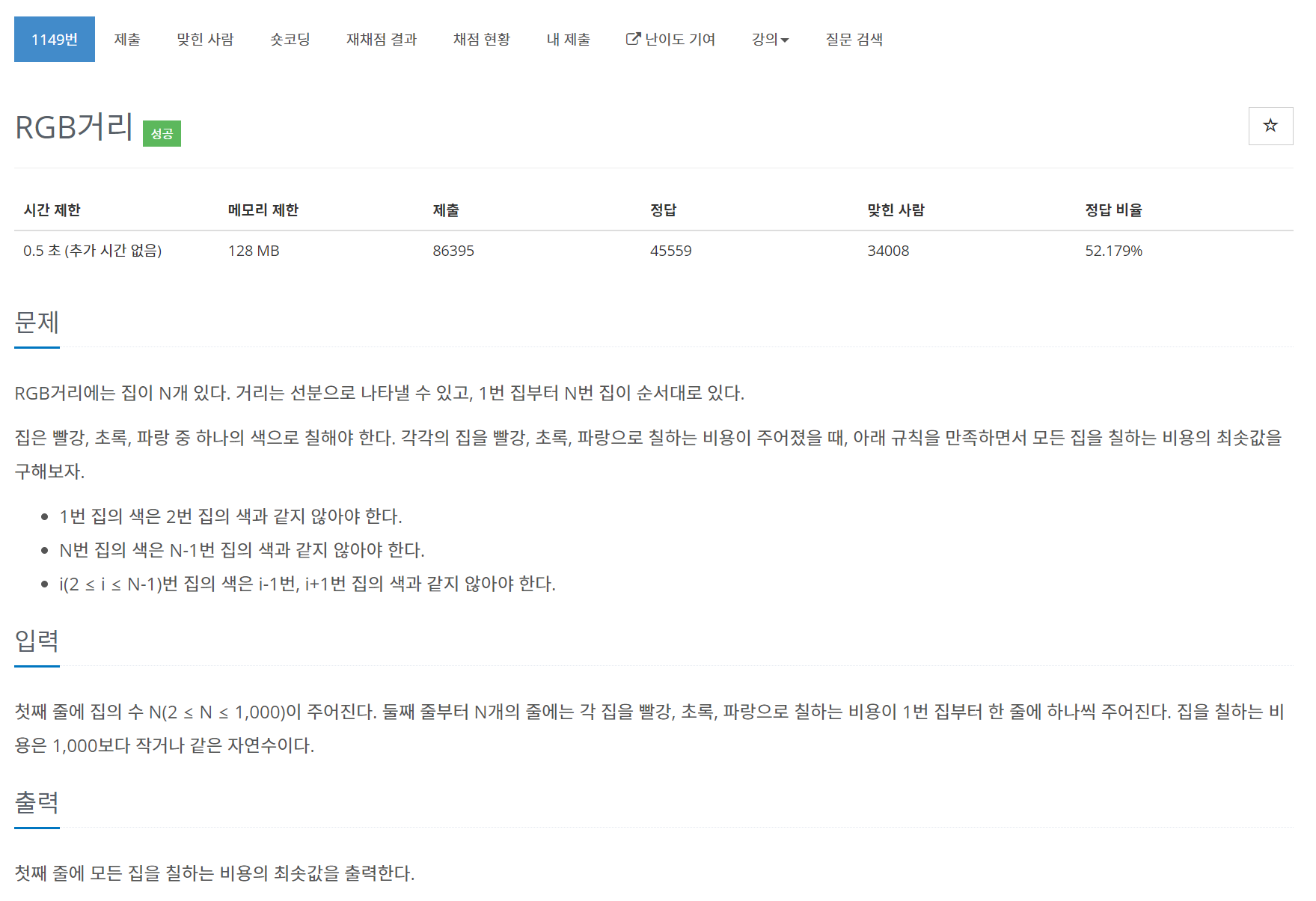
풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] arr = new int[n][3];
int[][] dp = new int[n][3];
for(int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j = 0; j < 3; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
}
}
// 1번째 집에 대한 데이터 추가
for(int j = 0; j < 3; j++) {
dp[0][j] = arr[0][j];
}
// 2번째 집 이후부터의 dp 계산
for(int i = 1; i < n; i++) {
dp[i][0] = Math.min(dp[i - 1][1], dp[i - 1][2]) + arr[i][0];
dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][2]) + arr[i][1];
dp[i][2] = Math.min(dp[i - 1][0], dp[i - 1][1]) + arr[i][2];
}
// 모두 칠한 뒤에 최저 비용 구하기
int min = Integer.MAX_VALUE;
for(int i = 0; i < 3; i++) {
if(dp[n - 1][i] < min) {
min = dp[n - 1][i];
}
}
System.out.println(min);
}
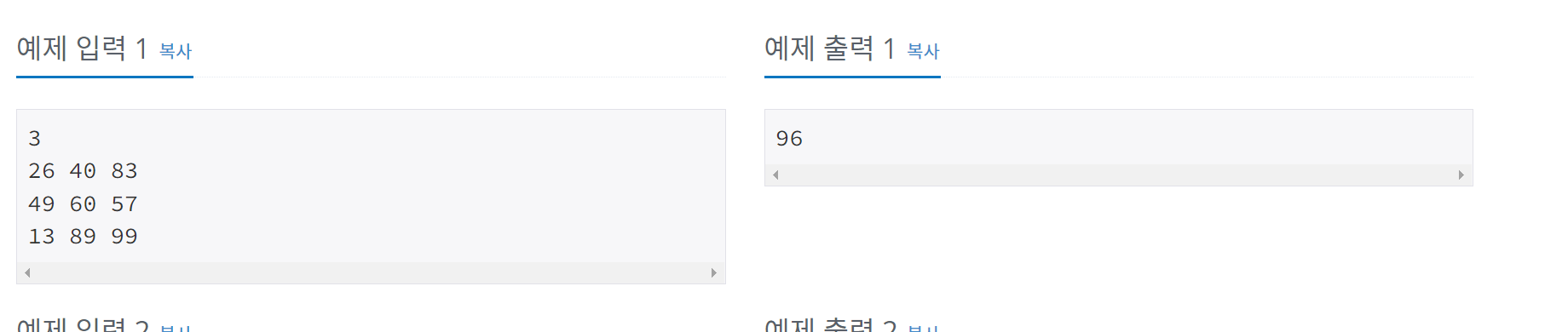
}11057번 오르막수
문제
풀이
0~9까지의 각 수(j)에서 만들 수 있는 오르막수는 이전 자릿수 n-1에서의 j부터 9까지의 합
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] dp = new int[n + 1][10];
for(int i = 0; i < 10; i++) {
dp[0][i] = 1;
}
for(int i = 1; i < n + 1; i++) {
for(int j = 0; j < 10; j++) {
for(int k = j; k < 10; k++) {
dp[i][j] += dp[i - 1][k];
dp[i][j] %= 10007;
}
}
}
System.out.println(dp[n][0] % 10007);
sc.close();
}
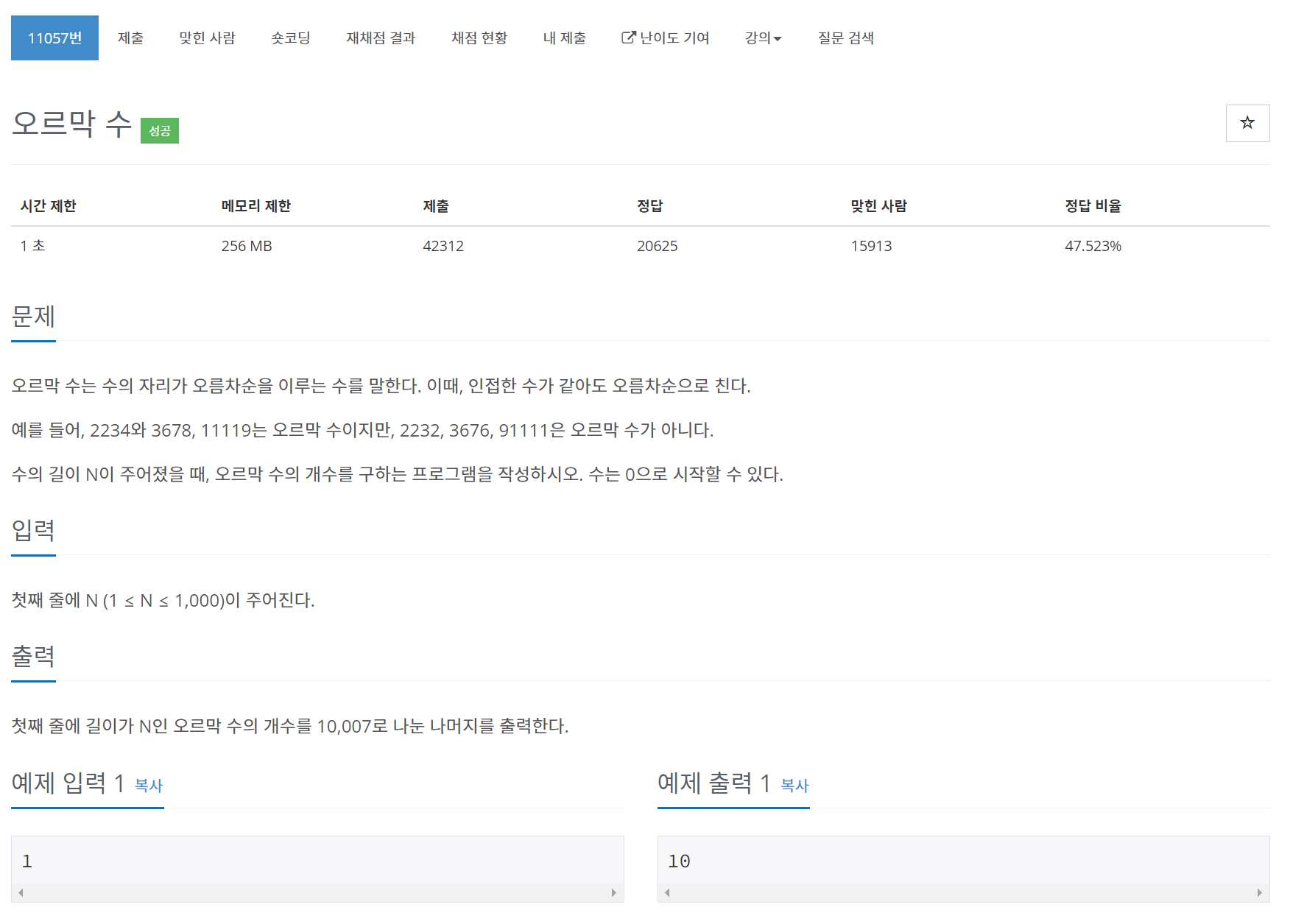
}11722번 가장 긴 감소하는 부분 수열
문제
풀이
dp에 각 원소 중에서 가장 긴 감소 수열의 길이를 담음.
현재 값이 이전 값보다 작으면 +1 씩 해서 담는다.
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int dp[] = new int[n + 1];
int arr[] = new int[n + 1];
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
for(int i = 1; i <= n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int answer = 0;
for(int i = 1; i <= n; i++) {
dp[i] = 1;
for(int j = 1; j < i; j++) {
if(arr[j] > arr[i]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
answer = Math.max(answer, dp[i]);
}
System.out.println(answer);
}
}13398번 연속합 2
문제
풀이
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
int n = Integer.parseInt(br.readLine());
int arr[] = new int[n];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int dp1[] = new int[n];
dp1[0] = arr[0];
int answer = dp1[0];
// 왼쪽->오른쪽으로 최대 연속 합을 저장
for (int i = 1; i < n; i++) {
dp1[i] = Math.max(dp1[i - 1] + arr[i], arr[i]);
answer = Math.max(answer, dp1[i]);
}
int dp2[] = new int[n];
dp2[n - 1] = arr[n - 1];
// 왼쪽->오른쪽으로 최대 연속 합을 저장
for (int i = n - 2; i >= 0; i--) {
dp2[i] = Math.max(dp2[i + 1] + arr[i], arr[i]);
}
// 특정 값이 지워졌다고 가정하여 오른쪽 방향과 왼쪽 방향의 최대 연속 합을 더함
// 더한 값과 answer를 비교하여 더 큰 값으로 교체
for (int i = 1; i < n - 1; i++) {
int temp = dp1[i - 1] + dp2[i + 1];
answer = Math.max(answer, temp);
}
bw.write(answer + "\n");
bw.flush();
bw.close();
br.close();
}
}