문제
twoSum함수에 숫자 리스트와 '특정 수'를 인자로 넘기면,더해서 '특정 수'가 나오는 index를 배열에 담아 return해 주세요.
nums: 숫자 배열
target: 두 수를 더해서 나올 수 있는 합계
return: 두 수의 index를 가진 숫자 배열
예를 들어,
nums은 [4, 9, 11, 14]
target은 13nums[0] + nums[1] = 4 + 9 = 13 이죠?
그러면 [0, 1]이 return 되어야 합니다.
가정
target으로 보내는 합계의 조합은 배열 전체 중에 2개 밖에 없다고 가정하겠습니다.
해답_1 (my solution)
def two_sum(nums, target):
for n in range(0,len(nums)):
for o in range(n+1, len(nums)):
if nums[n] + nums[o] == target :
return [n, o]한 요소에 대하여, 나머지 모든 요소를 각각 더해보면서 target을 찾도록 접근했다.
먼저 리스트의 모든 요소를 체크하는 for문을 작성하고, 요소를 모두 체크하기 위해서는 len으로 리스트의 길이를 구하고, range()에 대입했다.
다음은 n에 더해줄 값을 하나하나씩 대입하기 위해서 range(n+1,len(nums)) 을 작성하여 for 중첩문을 만들었다. 마지막으로 두개의 요소의 합을 구해서, target과 같은지를 비교해야 하여, 같으면 결과를 리턴한다.
해답_2 (model solution)
def two_sum(nums, target):
hash = {}
for i in range(len(nums)):
num = nums[i]
pair = target - num
if pair in hash:
return[hash[pair], i]
else:
hash[num] = i
return None합이 target인 num과 pair 두가지 요소를 찾는 방법으로, 요소 num의 pair는 target에서 num를 뺀 값이라고 연관지어 찾을 수 있다.
딕셔너리를 새로 생성하여, pair의 값이 저장되게 하고, for문을 통해 체크하고 있는 num의 pair가 딕셔너리에 저장되어 있을때, num과 pair를 리턴하는 방식으로 식을 세울수 있다.
for문으로 nums 리스트의 모든 요소(i)를 체크한다.
num은 nums의 요소를 순서대로 체크하도록, pair는 target에서 num의 값을 순서대로 뺀 값으로 변수를 선언했다.
다음으로 if문에서 pair를 딕셔너리에 저장하도록 코드를 작성한다.
예를 들어, nums = [2,4,6] ,target = 10이라고 가정하자.
딕셔너리 hash에 pair(target-num)가 존재하지 않을 경우, hash[num], 즉 첫번째 경우에는 hash[2] = 2 로 key&value 가 hash에 저장되게 된다.
다음에 체크할 요소인 4의 pair인 6도(10-4=6) hash에 존재하지 않으므로, hash[4] = 4 로 key&value가 저장된다.
다음 요소인 6의 pair인 4(10-6=4)는 hash에 이미 존재한다.따라서, hash[4], 즉 4 와 6을 리턴한다.
마지막으로, target을 만드는 요소가 존재하지 않을경우, None을 리턴한다.
해답_2가 더 적절한 이유를 알기위해서는 Big O Notation, time complexity에 대한 이해가 필요하다.
Time complexity
컴퓨터가 하나의 알고리즘을 풀기위하여 걸리는 시간을 뜻한다. 모든 elementary 작업을 처리하는데 같은 시간이 걸린다고 가정했을 때, elementary 작업의 수가 적을수록 시간은 적게 걸린다.
In computer science, the time complexity is the computational complexity that describes the amount of time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform.
linear search를 이용하여 리스트 [1,5,3,9,2,4,6,7,8]에서 하나의 요소를 찾는다고 가정해보자.
찾는 요소가 1일경우, 시간은 가장 적게 걸리므로 best-case다. 찾는 요소가 2일 경우는 average-case, 찾는 요소가 8일 경우는 worst-case로 볼 수 있다.
time complexity는 worst-case를 가정해서 생각해야 한다. 이 때 사용하는것이 Big-O notation 이다.
Big O notation
Big-O는 한 함수의 제한적인 행동을 설명할때 쓰이는 수학적 표현이다. 컴퓨터 공학에서는, input의 사이즈가 커지면서 걸리는 시간이나 필요한 메모리 용량이 얼마나 증가하는지를 나타낸다.
Big-O notation, sometimes called “asymptotic notation”, is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity.
다음은 Big-O를 사용하여 나타내는 time complexity의 종류이다.
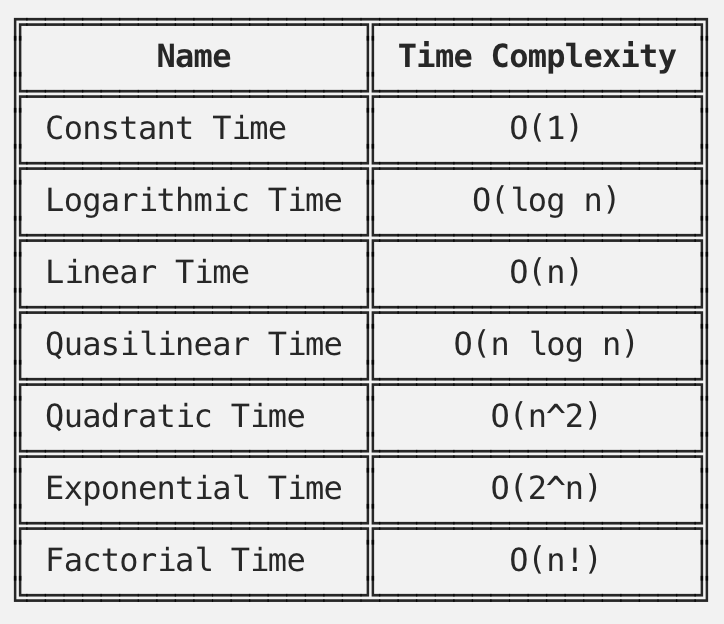
해답_1은 Quadratic Time에 해당한다. 즉, input데이터가 늘어날때마다, 걸리는 시간이 제곱으로 늘어난다. 예시에서 처럼, 각각의 요소(n)에 대해서 리스트에 있는 모든 요소(o)를 비교해보아야 하는 for중첩문의 경우, 여기에 해당된다.
반면에, 해답_2는 for문을 한번만 사용하기 때문에, linear time에 해당한다.즉 input데이터가 늘어날때마다, 처리에 걸리는 시간은 추가된 데이터 만큼만 늘어나게 된다. 알고리즘이 모든 값을 체크해야 할 경우, linear time이 최적의 선택이 된다.
이외의 각각의 complexity의 예제는 여기서 찾아볼 수 있다.
https://towardsdatascience.com/understanding-time-complexity-with-python-examples-2bda6e8158a7
