Java로 알고리즘 - [백준] 25307 시루의 백화점 구경

백준 25307 - 시루의 백화점 구경

원본 : https://www.acmicpc.net/problem/25307

문제

시루는 부모님과 함께 백화점에 갔다. 부모님은 쇼핑할 것이 많기 때문에 여러 곳을 돌아다녀야 하고, 시루는 부모님과 함께 걸어다니는 것이 너무 힘들어서 의자에 앉아서 쉬려고 한다.

백화점은 세로 길이가 $N$, 가로 길이가 $M$인 격자 형태이고, 상하좌우로 인접한 칸으로 이동할 때마다 1 만큼의 체력을 소모한다. 시루는 현재 위치에서 출발해 백화점 곳곳에 있는 의자 중 하나를 찾아가서 앉으려고 한다. 시루는 백화점 밖으로 나가면 부모님께 혼나기 때문에 백화점 밖으로 나갈 수 없다.

백화점에는 건물을 지탱하기 위한 기둥과 옷을 전시하기 위한 마네킹이 있다. 시루는 기둥이 있는 칸으로 이동하지 못하고, 마네킹을 무서워하기 때문에 마네킹과 거리가 $K$ 이하인 칸은 사용하지 않으려고 한다. 이때 두 칸 $(r_x, c_x), (r_y, c_y)$의 거리는 $\vert r_x-r_y \vert + \vert c_x-c_y \vert$이다. 단, 시루가 출발할 때는 부모님과 함께 있기 때문에, 출발 지점과 마네킹과의 거리가 $K$ 이하가 되어도 출발할 수 있다.

시루는 다리가 너무 아프기 때문에 체력 소모를 최소화하면서 의자까지 찾아가려고 한다. 시루가 소모하는 체력의 최솟값을 구해보자.

입력

첫째 줄에 백화점의 세로 길이, 가로 길이, 마네킹과 떨어져야 하는 거리를 의미하는 정수 $N, M, K$가 공백으로 구분되어 주어진다. ($1 \leq N,M \leq 2\,000$, $0 \leq K \leq 4\,000$)

둘째 줄부터 $N$개의 줄에 각각 $M$개씩 위에서부터 차례로 백화점의 상태가 주어진다. 아무것도 없는 칸은 0, 기둥이 있는 칸은 1, 의자가 있는 칸은 2, 마네킹이 있는 칸은 3, 시루의 시작 위치는 4로 주어진다. 시루의 시작 위치는 정확히 한 번 주어지고, 해당 위치에 기둥, 의자, 마네킹이 존재하지 않는다.

출력

시루가 의자를 찾아갈 수 있다면 시루가 소모하는 체력의 최솟값을 출력한다.

만약 의자를 찾아갈 수 없다면 -1을 출력한다.

Test Case

input

5 5 2
0 0 0 0 4
0 0 0 1 0
0 0 0 0 3
0 0 0 1 0
0 2 0 0 2

output

7

풀이

이전에 풀었던 영역탐색(BFS Search)로 해결하면 좋을 것 같다.
시작점(4)을 기준으로 기둥(1)과 마네킹(3)으로부터 $K$ 만큼 떨어져서 의자(2)까지 탐색하면서 걸린 최단 거리를 계산하면 된다.

우선, (3)을 기준으로 마네킹과의 거리를 반영해야 한다. 마네킹으로부터 K만큼 떨어진 거리는 지나가지 못하는 기둥(1)과 역할이 같으므로 기둥(1)로 치부해도 될 것 같다.
주의할 건, 마네킹으로 덮어지는 지역에 의자(2)가 있다면, 겁이 많은 시루는 도달하지 못한다고 했으니, 의자또한 기둥(1)으로 덮어질 것이다. 다만, 시작점(4)가 마네킹에 의해 덮어지는 지역에 있는 경우는 제외한다.

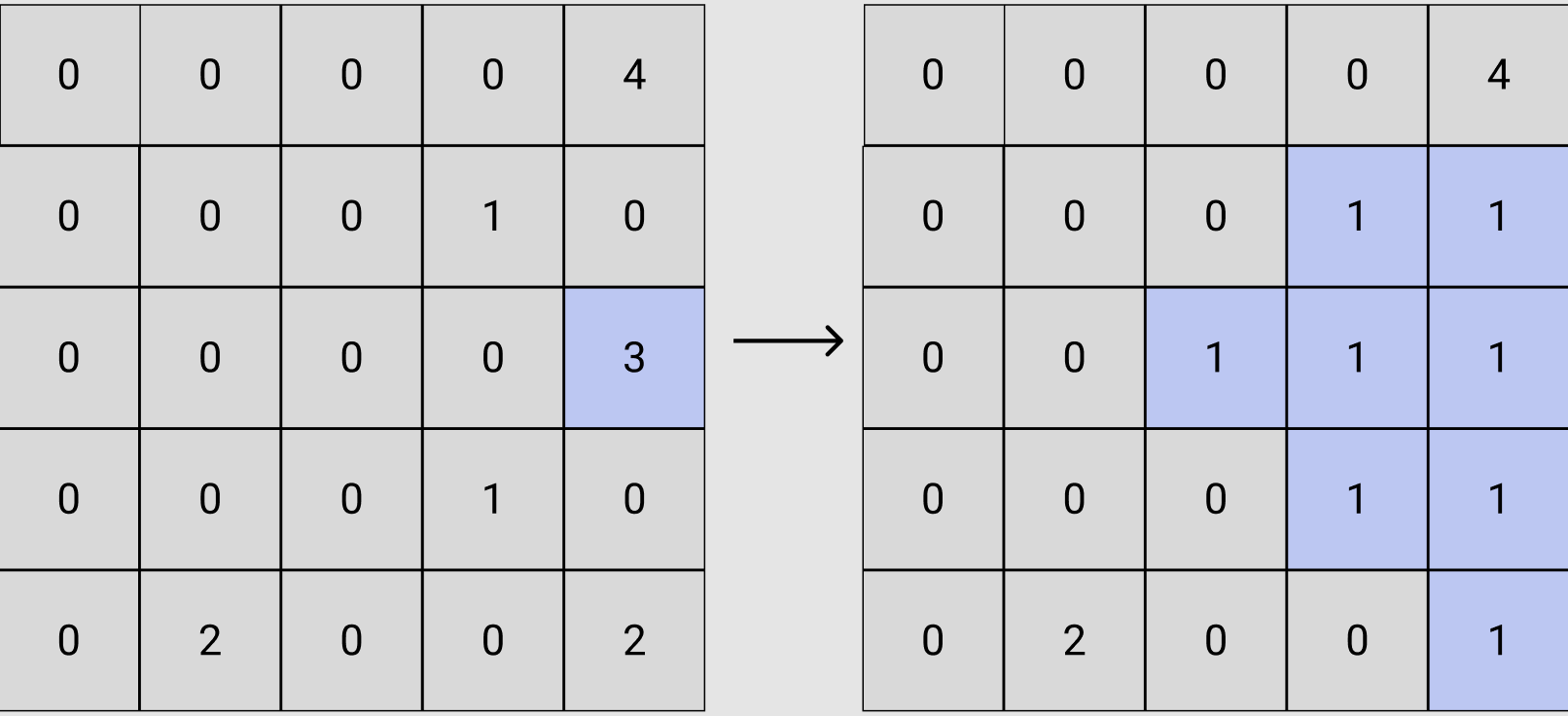
마네킹의 위치를 기준으로 BFS Search를 수행하며 지나갈 수 없는 지역을 적용한다. 이 때, 시작점인 마네킹과의 거리가 $K$인 경우까지만 수행한다.

마네킹으로부터 접근할 수 없는 영역 반영하기

public static void fillUnreachable(int y, int x, int[][] board) {
		Queue<int[]> queue = new LinkedList<>();

		queue.add(new int[]{y, x});

		board[y][x] = 1; //마네킹의 위치부터 변경

		while (!queue.isEmpty()) {
			int[] searchPoint = queue.poll();
			int startX = searchPoint[1];
			int startY = searchPoint[0];

			for (int i = 0; i < 4; i++) {
				int currentX = startX + dx[i];
				int currentY = startY + dy[i];

				//2차원 배열의 경계를 넘어서는 경우
				if (currentX < 0 || currentY < 0 || currentX >= M || currentY >= N) {
					continue;
				}
				
                //시작점이거나 이미 방문했던 경우
				if (board[currentY][currentX] == 4 || board[currentY][currentX] == 1) {
					continue;
				}
				
                //거리가 마네킹으로부터 K보다 큰 경우
				if (Math.abs(y - currentY) + Math.abs(x - currentX) > K) {
					continue;
				}
				
                //위 경우가 아니면 1로 덮는다.
				board[currentY][currentX] = 1;
				queue.add(new int[]{currentY, currentX});
			}
		}
	}

위 작업이 완료되었다면, 시작점에서 부터 의자가 있는 곳 까지 찾아가면 된다.
이전에 해결했던 문제에선 영역의 갯수를 구하고자 BFS Search가 이루어지는 횟수를 세었지만, 이번엔 한번의 BFS Search에서 진행하는 횟수를 구해야 한다.
일종의 Depth를 표기하기 위해, 필자는 현재 탐색중인 위치에 시작점으로부터의 거리를 저장하고, 다음 단계에서는 [이전 탐색위치 +1]을 저장하여 거리를 구하도록 하였다.

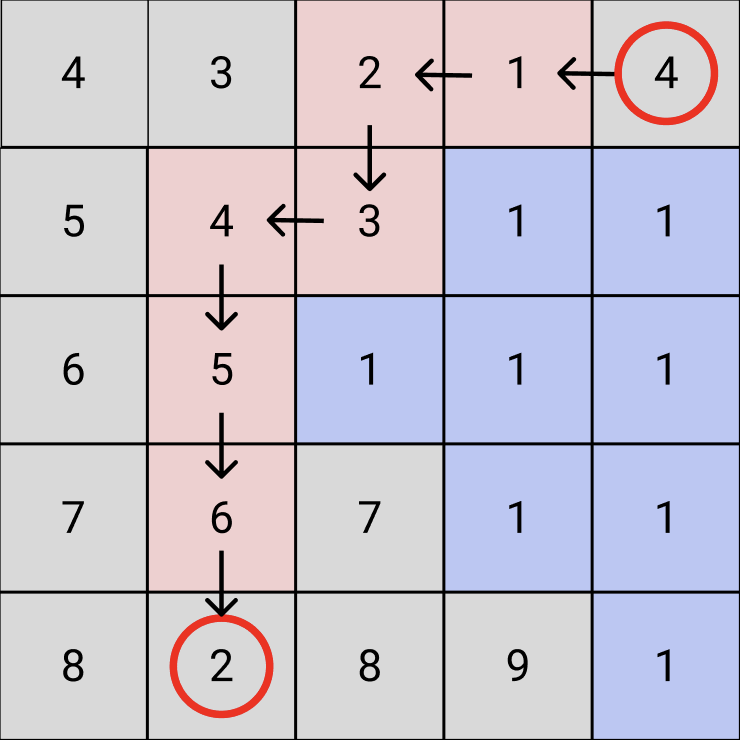
여기서 문제는 1이 두가지 의미를 가지게 된다. 기둥으로서 피해가야할 1과 시작점으로터 거리가 1이라는 의미를 가지기 때문이다.필자는 방문 여부를 저장하는 별도의 배열을 생성하지 않고, 위 중복되는 의미를 해소하기 위해 거리는 음수로 표현하기로 했다. -1, -2, ...-8

의자까지 최단거리 구하기

public static int moveOn(int y, int x, int[][] board) {
		Queue<int[]> queue = new LinkedList<>();
		queue.add(new int[]{y, x, 0}); //탐색 위치의 y, x 좌표와 함께 시작점으로터의 거리를 저장

		board[y][x] = -1; //초기위치 (4) 변경
        //초기 위치를 0이 아닌 -1로 하는 이유는
        //탐색과정에서 값이 0인 영역을 따라 가는데,
        //초기값이 0이면 지나간 지역임을 표기하지 못하기 때문
        
        //최단거리 반환시 -1이 시작이었던점을 반영해야함

		while (!queue.isEmpty()) {
			int[] movePoint = queue.poll();
			int startX = movePoint[1];
			int startY = movePoint[0];
			int distanceFromStart = movePoint[2] - 1; //이전 거리 -1

			for (int i = 0; i < 4; i++) {
				int currentX = startX + dx[i];
				int currentY = startY + dy[i];

				if (currentX < 0 || currentY < 0 || currentX >= M || currentY >= N) {
					continue;
				}
				
                //의자에 도착했다면,
				if (board[currentY][currentX] == 2) {
					return distanceFromStart; //-1부터 시작했기 때문에 추가적인 거리반영 없이 그냥 반환
				}

				//기둥도 아니고, 이미 지나온 곳이 아닌 경우 (0)
				if (board[currentY][currentX] == 0) {
					board[currentY][currentX] = distanceFromStart; //시작점과의 거리 반영
					queue.add(new int[]{currentY, currentX, distanceFromStart});
					continue;
				}
			}
		}

		return 1;
	}

정답 코드

package algorithms.week02;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class Boj_25307 {
	private static int[][] board;

	private static int[] dx = {-1, 0, 1, 0}; 
	private static int[] dy = {0, 1, 0, -1};

	private static int N;
	private static int M;
	private static int K;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		String NMK = br.readLine();
		StringTokenizer st = new StringTokenizer(NMK);

		N = Integer.parseInt(st.nextToken());
		M = Integer.parseInt(st.nextToken());
		K = Integer.parseInt(st.nextToken());

		board = new int[N][M];

		int startY = 0;
		int startX = 0;

		int[][] board = new int[N][M];
        //입력값 저장
		for (int i = 0; i < N; i++) {
			StringTokenizer nums = new StringTokenizer(br.readLine());
			for (int j = 0; j < M; j++) {
				int num = Integer.parseInt(nums.nextToken());
				if (num == 4) { //시작점 위치 저장
					startY = i;
					startX = j;
				}
				board[i][j] = num;
			}
		}

		for (int i = 0; i < N; i++) {
			for (int j = 0; j < M; j++) {
				if (board[i][j] == 3) {
                	//마네킹이 여러개 일 수 있음
					fillUnreachable(i, j, board);
				}
			}
		}

		int answer = moveOn(startY, startX, board);

		//거리를 음수로 표현했기 때문에 -1을 곱하여 출력한다
		System.out.println(answer * (-1));

	}

	public static void fillUnreachable(int y, int x, int[][] board) {
		Queue<int[]> queue = new LinkedList<>();

		queue.add(new int[]{y, x});

		board[y][x] = 1; //마네킹의 위치부터 변경

		while (!queue.isEmpty()) {
			int[] searchPoint = queue.poll();
			int startX = searchPoint[1];
			int startY = searchPoint[0];

			for (int i = 0; i < 4; i++) {
				int currentX = startX + dx[i];
				int currentY = startY + dy[i];

				//2차원 배열의 경계를 넘어서는 경우
				if (currentX < 0 || currentY < 0 || currentX >= M || currentY >= N) {
					continue;
				}
				
                //시작점이거나 이미 방문했던 경우
				if (board[currentY][currentX] == 4 || board[currentY][currentX] == 1) {
					continue;
				}
				
                //거리가 마네킹으로부터 K보다 큰 경우
				if (Math.abs(y - currentY) + Math.abs(x - currentX) > K) {
					continue;
				}
				
                //위 경우가 아니면 1로 덮는다.
				board[currentY][currentX] = 1;
				queue.add(new int[]{currentY, currentX});
			}
		}
	}

	public static int moveOn(int y, int x, int[][] board) {
		Queue<int[]> queue = new LinkedList<>();
		queue.add(new int[]{y, x, 0}); //탐색 위치의 y, x 좌표와 함께 시작점으로터의 거리를 저장

		board[y][x] = -1; //초기위치 (4) 변경
        //초기 위치를 0이 아닌 -1로 하는 이유는
        //탐색과정에서 값이 0인 영역을 따라 가는데,
        //초기값이 0이면 지나간 지역임을 표기하지 못하기 때문
        
        //최단거리 반환시 -1이 시작이었던점을 반영해야함

		while (!queue.isEmpty()) {
			int[] movePoint = queue.poll();
			int startX = movePoint[1];
			int startY = movePoint[0];
			int distanceFromStart = movePoint[2] - 1; //이전 거리 -1

			for (int i = 0; i < 4; i++) {
				int currentX = startX + dx[i];
				int currentY = startY + dy[i];

				if (currentX < 0 || currentY < 0 || currentX >= M || currentY >= N) {
					continue;
				}
				
                //의자에 도착했다면,
				if (board[currentY][currentX] == 2) {
					return distanceFromStart; //-1부터 시작했기 때문에 추가적인 거리반영 없이 그냥 반환
				}

				//기둥도 아니고, 이미 지나온 곳이 아닌 경우 (0)
				if (board[currentY][currentX] == 0) {
					board[currentY][currentX] = distanceFromStart; //시작점과의 거리 반영
					queue.add(new int[]{currentY, currentX, distanceFromStart});
					continue;
				}
			}
		}

		return 1;
	}
}