Java BigDecimal로 정확한 숫자 표현하기

원태연·2023년 3월 14일

보너스 돈이 생겼다

블랙잭을 마치고 환전을 하러갔다.
기분 좋게 [4.98달러]칩 8개와 [0.99달러]칩 5개를 교환하려했다.

private static final double BIG_CHIP_REFUND_DOLLAR = 4.98d;
private static final double SMALL_CHIP_REFUND_DOLLAR = 0.99d;

void exchange() {
    double accountDollar = 0d;
    int bigChipCount = 8;
    for (int i = 0; i < bigChipCount; i++) {
        accountDollar += BIG_CHIP_REFUND_DOLLAR;
    }

    int smallChipCount = 5;
    for (int i = 0; i < smallChipCount; i++) {
        accountDollar += SMALL_CHIP_REFUND_DOLLAR;
    }
    System.out.println("accountDollar : " + accountDollar);
}

실행결과

0.0000...01 달러가 붙었다. 다룬 적 없는 자릿수에서 값이 추가된게 조금 이상하다.

부동 소수점

위와 같은 결과가 나타난 이유는 십진수의 소숫점을 이진수로 표현하기 위한 노력의 결과이기도 하다.
비트로 수를 표현하는 컴퓨터에게 십진수의 상세한 소숫점을 표현하기엔 힘든점이 있다.

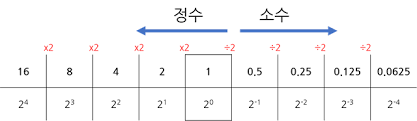
위 이미지를 참고해보면 십진수 소숫점의 변환은 다음과 같다

$0.5$ = $2^{-1}$ ==> 0.1
$0.25$ = $2^{-2}$ ==> 0.01

이렇게 딱 떨어지는 수에 대해선 큰 고민을 하지 않아도 되지만, 십진수 $0.3$ 은 어떻게 표현해야 할까?
일반적인 공식을 활용하면 십진수 $0.3$ 은 $0.01001100110011...$ (0011)의 무한 반복이라고 한다. 결국 정확한 값이 아닌 근사치로 변환이 가능한 수들이 존재한다.

$1.3$ 과 같은 소수(小數)를 이진수로 표현하기 위해선, 십진수 체계와 동일하게 정수부와 소수부를 구분하여 표현할 수 있다.
4byte(32bit)를 사용하는 체계에서 표현하면 16bit, 16bit를 나누어 표현해도 좋지만, $(00...0001.010011001100110)$ 고정된 크기로 정수부와 소수를 나누는 건 비효율적이다.

정수부의 bit를 늘리면 큰 숫자를 표현할 수 있지만 정밀한 숫자를 표현하기 어렵고, 반대로 소수부의 bit를 늘릴 경우 정밀한 숫자를 표현할 수 있지만 큰 숫자를 표현하지 못한다.

1.23123123123 혹은 12312312312.3 과 같이 성격(?)이 다른 두 수에 효율성이 떨어진다.

부동(浮動) 소수점

위와 같은 문제를 해결하기 위해 변환하는 숫자에 따라 소수점이 고정되어있지 않고 부동하여 결정되는 방식이 제안되었다.

자세한건 자료가 많으니 검색해서 찾아보자. 간단하게 말하면, 정수부/소수부의 분리가 아닌 소수점을 앞으로 옮겨 지수(exponential)부/가수부로 저장하는 방식이다.

ex)

$263.3$ => 100000111.010011001100110...
=> 1.00000111010011001100110... * $2^8$

지수부: 100000111
가수부: 00000111010011001100110...

효율이야 높아졌더라도, 근사치를 저장하는건 마찬가지라는 점을 확인하는 것이 포인트.

BigDecimal

이러한 특징이 환전해가는 고객에게 보너스 금액이 붙어간 것이다. 매우 작은 값이지만, 매일 환전 요청이 100만건을 넘으면 무시할 수 있는가?
IEEE 754 부동 소수점 방식을 사용하는Java에선 돈이나 소숫점을 다룬다면 BigDecimal을 사용하는 것은 필수적이다.

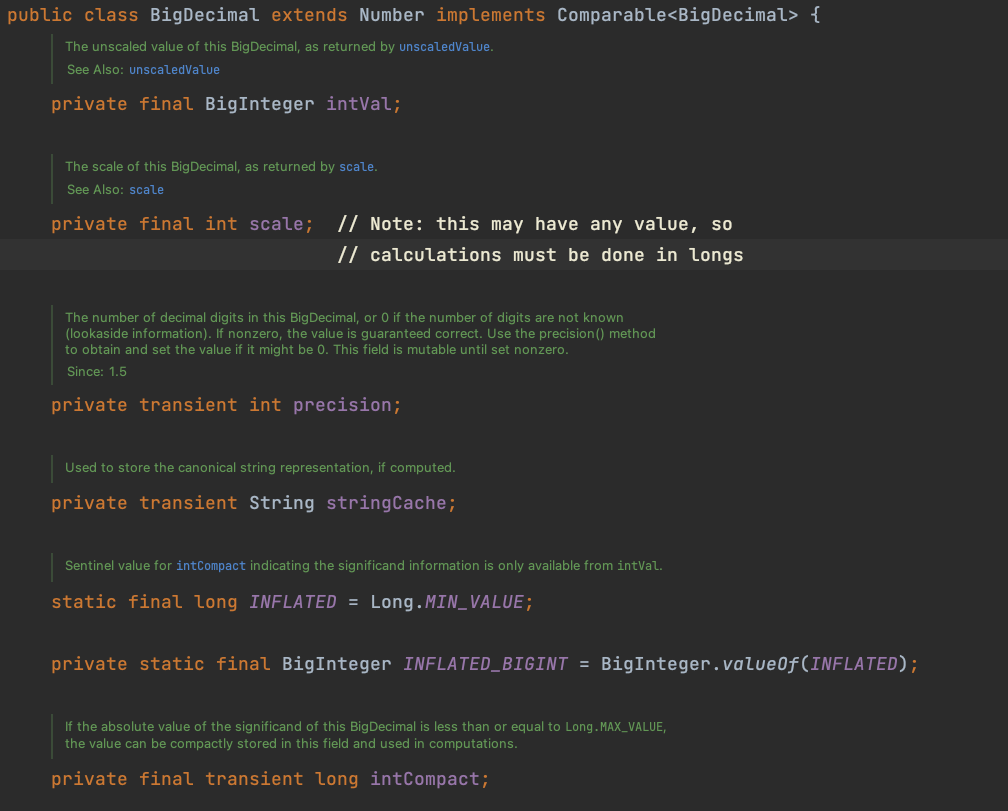
BigDecimal.class는 java.math 패키지에 위치한다. 쉽게 접근하여 확인할 수 있는데, 얼핏 보이는 특징으로는 Number를 상속한 "클래스"라는 점이다. 또 필드들이 final 키워드를 가진것을 보아하니 Integer나 Double과 같은 불변 클래스라는 점도 유추할 수 있다.

초기화

숫자를 포장한 객체 처럼 사용해도 좋지만, 중요한 점이 있다. 수를 사용하여 생성할 수 있지만, 권장하지 않는다.

@Test
void test() {
    BigDecimal doubleA = new BigDecimal(0.34d);
    BigDecimal doubleB = new BigDecimal("0.34");

    assertThat(doubleA).isEqualTo(doubleB);
}

위 테스트의 결과는 난해한 결과와 함께 실패한다.

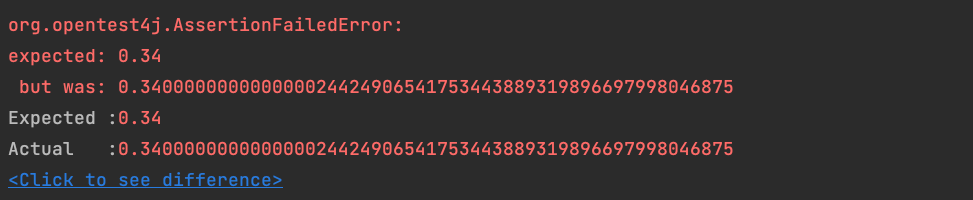
우리가 인식한 문제의 방식을 동일하게 사용하며 해결책을 채택한다면 무슨 소용이 있겠는가.
꼭! 문자열로 생성하여 기대하는 장점을 얻도록 하자.

인텔리제이도 쓰지 말라한다.

비교

.equals()를 사용하여 동등성을 비교할 수 있다.

@Test
void test() {
    BigDecimal doubleB = new BigDecimal("0.34");
    BigDecimal doubleC = new BigDecimal("0.34");

    assertThat(doubleB.equals(doubleC)).isTrue(); //통과
}

흥미로운점은 아래 상황과 같다.

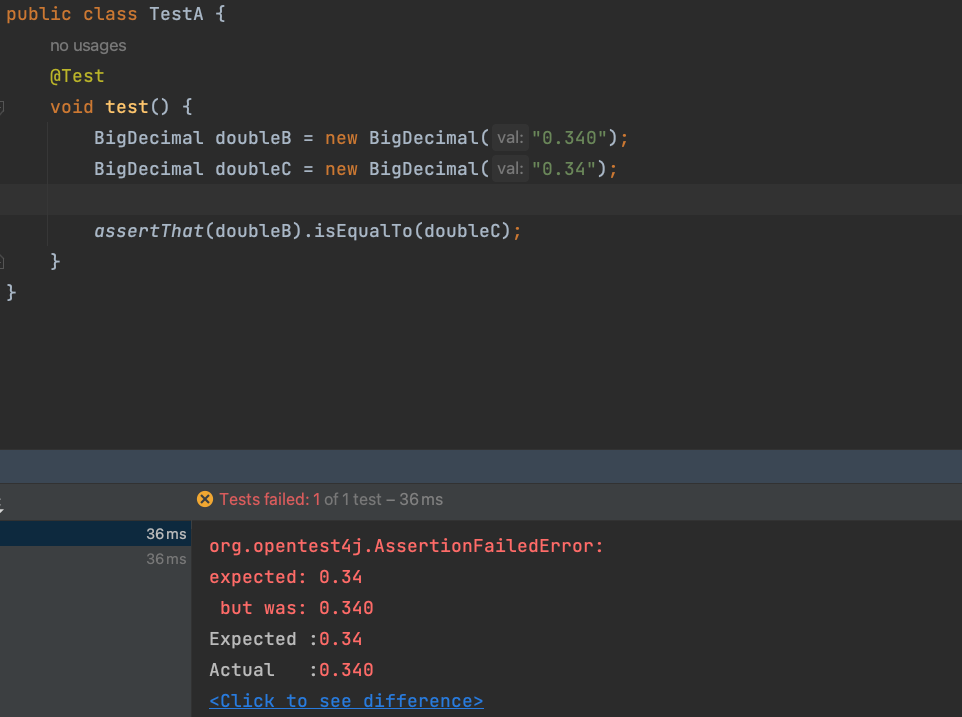
equals 사용시 자릿수(scale)에 주의해서 꼼꼼하게 쓰도록하자.

또 크기 비교는 앞에서 살펴보았듯이 Comparable<BigDecimal>을 구현하고 있기에
.compareTo()를 사용할 수 있다.
a.compareTo(b)를 사용했을 때,

a > b ==> 1
a = b ==> 0
a < b ==> -1

의 결과를 기대할 수 있다.

@Test
void test() {
    BigDecimal small = new BigDecimal("0.3");
    BigDecimal middle = new BigDecimal("0.34");
    BigDecimal big = new BigDecimal("0.345");
    BigDecimal big2 = new BigDecimal("0.345");

    System.out.println(small.compareTo(middle)); // -1
    System.out.println(big.compareTo(small)); // 1
    System.out.println(big.compareTo(big2)); // 0
}

재밌는 점은 아래와 같은 경우다

@Test
void test() {
    BigDecimal small = new BigDecimal("0.340");
    BigDecimal middle = new BigDecimal("0.34");

    assertThat(small.equals(middle)).isFalse();
    assertThat(small.compareTo(middle)).isEqualTo(0);
}

equals는 다르다고 하는데, compareTo의 결과는 0이 나온다. 내부 구현을 살펴보면 scale을 사용하여 비교하는 지에 따라 결과가 다른 것 같다. Stream이나 Collection에 사용되기 위한 Comparable의 구현과 동등성의 의미를 다르게 보는 것 같았다.

타입 변환

BigDecimal은 Number를 구현하고 있기에 XXXValue()를 사용하여 반환 할 수 있다.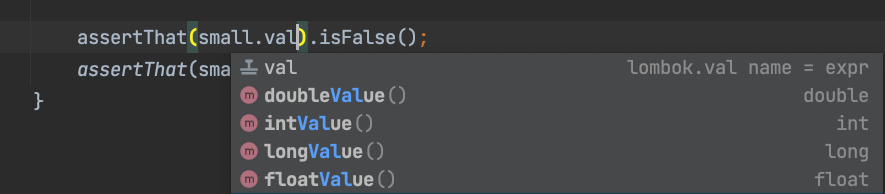
정확한 타입 변환을 보장하고 싶다면 XXXValueExact()를 사용하면 된다.

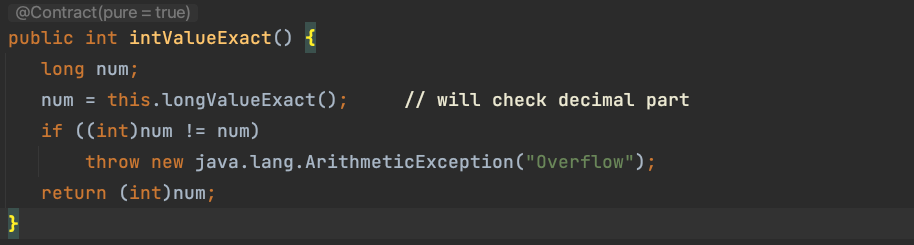
@Test
void test() {
    BigDecimal small = new BigDecimal("34.1");

    assertThat(small.intValue()).isEqualTo(34);
    assertThatThrownBy(() -> small.intValueExact())
            .isInstanceOf(ArithmeticException.class);
}

연산

큰 설명 없이 코드로 확인할 수 있다. 주의할 점은, BigDecimal은 앞서 말했듯이 불변 객체이기 때문에 계산 결과로 새로운 인스턴스를 반환한다는 점이다.

@Test
void test() {
    BigDecimal small = new BigDecimal("3.1");
    BigDecimal big = new BigDecimal("5");
    BigDecimal mod = new BigDecimal("2");

    BigDecimal add = small.add(big);           // +
    BigDecimal subtract = big.subtract(small); // -
    BigDecimal multiply = big.multiply(small); // *
    BigDecimal divide = big.divide(mod);       // /
    BigDecimal remainder = big.remainder(mod); // %

    assertThat(add).isEqualTo(new BigDecimal("8.1"));
    assertThat(subtract).isEqualTo(new BigDecimal("1.9"));
    assertThat(multiply).isEqualTo(new BigDecimal("15.5"));
    assertThat(divide).isEqualTo(new BigDecimal("2.5"));
    assertThat(remainder).isEqualTo(new BigDecimal("1"));
}