백준 1010 - 다리 놓기

원본 : https://www.acmicpc.net/problem/1010

문제

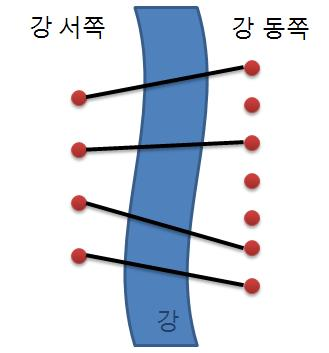
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)

재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.

Test Case

input

3
2 2
1 5
13 29

output

1
5
67863915

풀이

한 사이트에는 최대 한개의 다리만 이을 수 있고, 최대한 많은 다리를 설치하는 경우의 수를 구하는 것이 목적.
최대로 설치하기 위해선, 서쪽 사이트를 기준으로 다리를 놓을 동쪽 사이트를 결정하면 된다. 서쪽 사이트가 동쪽 사이트보다 항상 작거나 같으므로 (N ≤ M), 동쪽의 사이트들 중에서 서쪽 사이트 만큼 선택되는 경우의 수를 구하면 된다.

M개에서 N개를 순서와 상관없이 선택하는 경우의 수 => 조합 $_mC_n$ 을 활용하면 된다.

조합 공식

$_mC_n = \frac {m!}{n!(m-n)!}$

예를 들어
5, 3인 경우, $\frac {5!}{3!·2!}$ 이고, => $\frac {5·4}{2·1}$ 이고,
7, 4인 경우, $\frac {7!}{4!·3!}$ 이고, => $\frac {7·6·5}{3·2·1}$ 이다.

단순하게, $m$부터 $m - n$까지 곱을 $n!$만큼 나누면 된다.

구현 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Boj_1010 {
	public void solution() throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int T = Integer.parseInt(br.readLine());

		for (int i = 0; i < T; i++) {
			long answer = getAnswer(br);
			System.out.println(answer);
		}
	}

	private long getAnswer(BufferedReader br) throws IOException {
		StringTokenizer st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());

		long answer = 1;
		//mCn
		for (int i = (M - N) + 1; i <= M; i++) {
			answer *= i;
		}
		for (int i = 1; i <= N; i++) {
			answer /= i;
		}
		return answer;
	}
}

$_mC_n$ 부분을 보면,
m - n + 1부터 m까지 곱을 구한 뒤
n!만큼 나누었다.

그리고 틀렸다!

틀린 이유는 단순했다. N, M이 최대 30이라는 점이다.
입력이 1 30 인 경우 $_{30}C_{1}$을 구해야 한다. 간단히 30이라는 것을 알지만, 위 과정으로 진행하면, answer에 1부터 30까지 곱한 값이 우선적으로 저장되어야 한다. $15!$ 만 하더라도 10조를 넘어간다. 실제로 answer의 값을 보면 오버플로우 되어 음수가 되어버렸다.

다이나믹 프로그래밍

다른 방식으로 다이나믹 프로그래밍을 생각해봤다.
$_5C_2$와 $_5C_3$의 차이를 보자.

$\frac {5·4}{2·1}$, $\frac {5·4·3}{3·2·1}$이다.
다음으로 $_5C_4$를 살펴보면 $\frac {5·4·3·2}{4·3·2·1}$이다.
$_mC_n$과 $_mC_{n-1}$의 관계가 보이지 않는가..?!

$_mC_{n-1}$의 값에서 ($m-n+1$)을 곱하고, $n$을 나누면 $_mC_n$이 된다!

정답 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Boj_1010 {
	public void solution() throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int T = Integer.parseInt(br.readLine());

		for (int i = 0; i < T; i++) {
			long answer = getAnswer(br);
			System.out.println(answer);
		}
	}

	private long getAnswer(BufferedReader br) throws IOException {
		StringTokenizer st = new StringTokenizer(br.readLine());
		int N = Integer.parseInt(st.nextToken());
		int M = Integer.parseInt(st.nextToken());

		long[] memo = new long[M + 1];
		memo[1] = M;
		//mCn
		for (int i = 2; i <= N; i++) {
	        //(n-1)항과 n항 과의 관계
			memo[i] = (memo[i - 1]) * (M - i + 1) / i;
		}
		return memo[N];
	}
}

오버플로우도 방지했지만, 성능 부분에서도 상향되었다.
$O(2n)$ => $O(n)$