이진 탐색 트리

원태연·2022년 5월 30일

algorithm datastructure

Binary Search Tree

이진 탐색 트리

이진 탐색 트리는 이진트리의 일종으로, 데이터를 특정한 규칙으로 저장하여 원하는 데이터의 위치를 찾는데 사용가능 하다.

데이터의 저장 규칙

이진 탐색 트리의 노드에 저장된 키(Key)는 유일하다.
루트 노드의 키가 왼쪽 서브 트리를 구성하는 어떠한 노드의 키보다 크다.
루트 노드의 키가 오른쪽 서브 트리를 구성하는 어떠한 노드의 키보다 작다.
왼쪽과 오른쪽 서브트리도 이진 탐색 트리이다.

ex)

데이터 추가

위 저장규칙을 따르도록 데이터를 추가하려면, 자료구조 내에서 데이터의 올바른 위치를 찾아가면 된다.

'작으면 왼쪽, 크면 오른쪽'이라는 규칙을 준수하며 데이터를 추가한다.

데이터 삽입

void BSTInsert(BTreeNode **pRoot, BSTData data) {
  //이진탐색트리라는 구조체의 노드를 가리키기 위해 이중 포인터 사용
    BTreeNode *pNode = NULL; 
    BTreeNode *cNode = *pRoot;
    BTreeNode *nNode = NULL;

    while(cNode != NULL) { //cNode == NULL이면 단말 노드까지 간 경우이다.
        if(GetData(cNode) == data) //중복은 허용X
            return;

        pNode = cNode;

        if(GetData(cNode) > data)
            cNode = GetLeftSubTree(cNode); //추가하려는 Data가 작으면 왼쪽
        else
            cNode = GetRightSubTree(cNode); //추가하려는 Data가 크면 오른쪽
    }
  
  //현재 pNode는 추가되어야할 위치의 부모 노드
  
  //자식노드 생성
    nNode = MakeBTreeNode();
    SetData(nNode, data);

  //추가되어야 할 부모 노드와 비교하여 작으면 왼쪽, 크면 오른쪽으로 자식 노드 추가
    if(pNode != NULL) { 
        if(GetData(pNode) > data)
            MakeLeftSubTree(pNode, nNode);
        else
            MakeRightSubTree(pNode, nNode);
    }
    else {//루트 노드가 존재하지 않으면
        *pRoot = nNode;
    }
}

새로 추가될 데이터와 이미 존재하는 이진 탐색 트릭의 데이터들을 비교하여 추가되어야할 위치를 찾는다.
찾은 위치의 부모노드와 마지막으로 비교하여 규칙(작으면 왼쪽, 크면 오른쪽)에 맞게 삽입한다.

이러한 로직을 통해 데이터를 추가하면 규칙에 맞게 알아서 위치를 찾아가도록 구현할 수 있다.

이는 탐색과도 이어진다.
찾으려는 데이터와 이진 탐색 트리를 비교할 때, 위 로직과 동일하게 수행하면 해당 데이터의 위치로 이동할 수 있고, 만약 존재하지 않는 값이라면 NULL일 것 이다.

데이터 탐색

BTreeNode *BSTSearch(BTreeNode *bst, BSTData target) {
    BTreeNode *cNode = bst;
    BSTData cd;

    while(cNode != NULL) {
        cd = GetData(cNode);

        if(target == cd)
            return cNode; //해당 위치까지 도달하여 존재하면 값 return
        else if(target < cd)
            cNode = GetLeftSubTree(cNode);
        else
            cNode = GetRightSubTree(cNode);
    }

    return NULL; //해당 위치까지 도달 후 존재하지 않는 다면 NULL
}

데이터 삭제

이진 탐색 트리의 삭제는 동일한 데이터에 대해서도 노드의 위치에 따라 다음과 같은 경우가 존재한다.

삭제할 노드가 단말 노드인 경우
삭제할 노드가 하나의 자식 노드를(하나의 서브 트리를) 갖는 경우
삭제할 노드가 두개의 자식 노드를(두 개의 서브 트리를) 갖는 경우

1. 삭제할 노드가 단말 노드인 경우

단순히 해당 노드를 해제하면 된다.

dNode = cNode;

if(GetLeftSubTree(dNode) == NULL && GetRightSubTree(dNode) == NULL) { //단말노드인 경우
  //dNode는 삭제할 노드
  
    if(GetLeftSubTree(pNode) == dNode)
        RemoveLeftSubTree(dNode);
    else
        RemoveRightSubTree(dNode);
}

이미지 출처

2. 삭제할 노드가 하나의 자식 노드를 갖는 경우

자식노드가 하나인 경우, 해당 자식 노드를 삭제할 노드의 부모노드와 연결하고 메모리에서 해제(삭제) 한다.

else if(GetLeftSubTree(dNode) == NULL || GetRightSubTree(dNode) == NULL) {
  //dNode는 삭제할 노드
  
  BTreeNode *dcNode;

  if(GetLeftSubTree(dNode) != NULL)
    dcNode = GetLeftSubTree(dNode);
  else
    dcNode = GetRightSubTree(dNode);

  if(GetLeftSubTree(pNode) == dNode)
    ChangeLeftSubTree(pNode, dcNode);
  else
    ChangeRightSubTree(pNode, dcNode);
}

이미지 출처

3. 삭제할 노드가 두개의 자식 노드를 갖는 경우

삭제로 인해 비는 위치를 무엇으로 채워야 할까?

왼쪽 서브트리에서 가장 큰 값

OR
오른쪽 서브트리에서 가장 작은 값

예시)

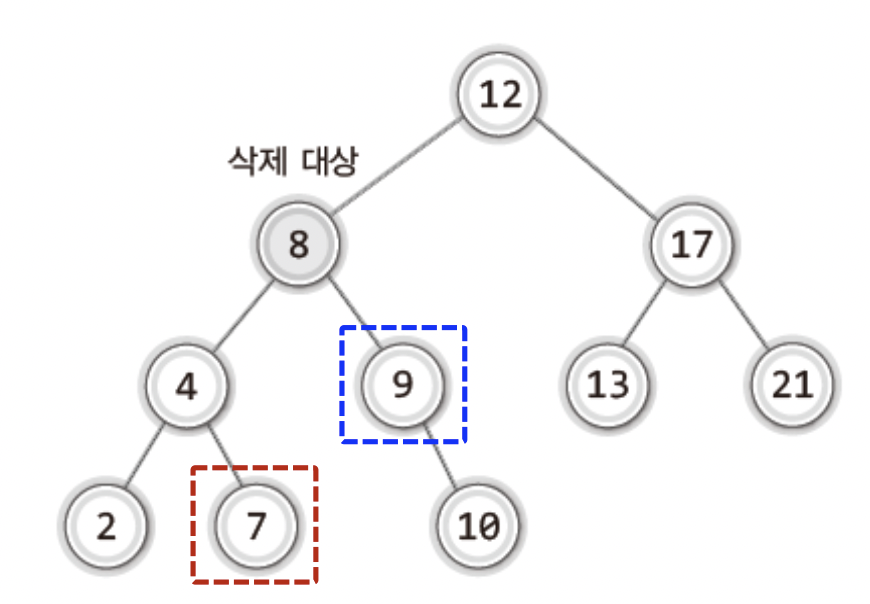
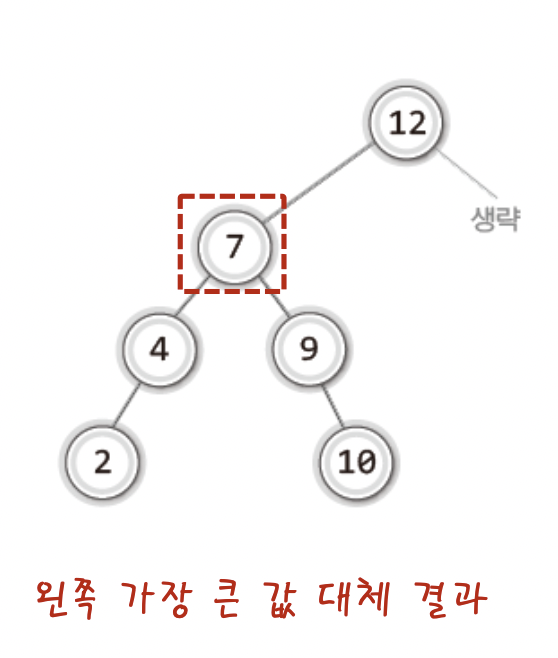
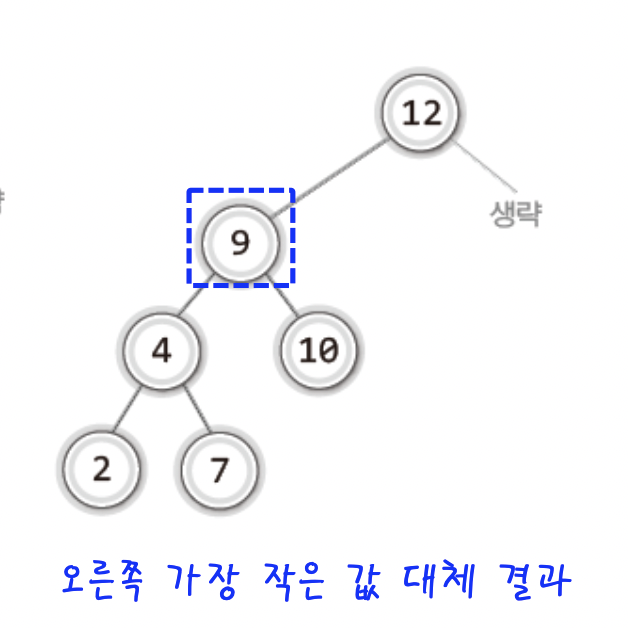
두 가지 방식 모두 사용하여도 이진 탐색 트리를 유지하는 것을 알 수 있다.

구현

else if(GetLeftSubTree(dNode) != NULL || GetRightSubTree(dNode) != NULL) { //서브트리가 두 개인 경우
  //dNode는 삭제할 노드
  //두 가지 방법 중 오른쪽 서브트리의 최솟값으로 대체하는 로직
  
  BTreeNode *mNode = GetRightSubTree(dNode); //대체할 노드, 오른쪽 서브트리의 루트노드로 시작
  BTreeNode *mpNode = dNode; //대체할 노드의 부모 노드
  int delData;

  //대체 노드 탐색(왼쪽 서브트리로 계속 이동하여 최솟값에 도달(단말노드))
  while(GetLeftSubTree(mNode) != NULL) {
    mpNode = mNode;
    mNode = GetLeftSubTree(mNode);
  }

  delData = GetData(dNode);
  SetData(dNode, GetData(mNode));

  //대체가 완료되어 사라질 노드의 부모 노드와 자식노드를 연결
  //상황 2와 유사
  if(GetLeftSubTree(mpNode) == mNode) {
    ChangeLeftSubTree(mpNode, GetRightSubTree(mNode));
  } else {
    ChangeRightSubTree(mpNode, GetRightSubTree(mNode));
  }

  dNode = mNode;
  SetData(dNode, delData); //데이터 대체
}

전체코드 (remove)

BTreeNode *BSTRemove(BTreeNode **pRoot, BSTData target) {
  
		//삭제 대상이 루트 노드인 경우를 위해 존재
  	//가상 루트 노드
    BTreeNode *pVRoot = MakeBTreeNode();  

    BTreeNode *pNode = pVRoot; 
    BTreeNode *cNode = *pRoot;
    BTreeNode *dNode;

  //실제 루트 노드를 가상 노드의 오른쪽 서브트리로 지정
  //자료구조에서 Dummy를 쓰는 것과 유사
    ChangeRightSubTree(pVRoot, *pRoot);

  //삭제할 대상인 노드 탐색
    while(cNode != NULL && GetData(cNode) != target) {
        pNode = cNode;

        if(target < GetData(cNode))
            cNode = GetLeftSubTree(cNode);
        else
            cNode = GetRightSubTree(cNode);
    }

    if(cNode == NULL) {//삭제 대상이 없는 경우
        return NULL;
    }

    dNode = cNode;

  //상황 1.
  //단말 노드인 경우
    if(GetLeftSubTree(dNode) == NULL && GetRightSubTree(dNode) == NULL) {
        if(GetLeftSubTree(pNode) == dNode) {
            RemoveLeftSubTree(dNode);
        } else {
            RemoveRightSubTree(dNode);
        }
    } 
  //상황 2.
  //하나의 서브트리가 있는 경우
	  else if(GetLeftSubTree(dNode) == NULL || GetRightSubTree(dNode) == NULL) {
        BTreeNode *dcNode;

        if(GetLeftSubTree(dNode) != NULL) {
            dcNode = GetLeftSubTree(dNode);
        } else {
            dcNode = GetRightSubTree(dNode);
        }
        
	      if(GetLeftSubTree(pNode) == dNode) {
            ChangeLeftSubTree(pNode, dcNode);
        } else {
            ChangeRightSubTree(pNode, dcNode);
        }
    }
  
  //상황 3.
  //두 개의 서브트리가 존재하는 경우
    else {
        BTreeNode *mNode = GetRightSubTree(dNode);
        BTreeNode *mpNode = dNode;
        int delData;

        while(GetLeftSubTree(mNode) != NULL) {
            mpNode = mNode;
            mNode = GetLeftSubTree(mNode);
        }

        delData = GetData(dNode);
        SetData(dNode, GetData(mNode));

        if(GetLeftSubTree(mpNode) == mNode) {
            ChangeLeftSubTree(mpNode, GetRightSubTree(mNode));
        } else {
            ChangeRightSubTree(mpNode, GetRightSubTree(mNode));
        }

        dNode = mNode;
        SetData(dNode, delData);
    }

  //삭제된 노드가 루트 노드인 경우
    if(GetRightSubTree(pVRoot) != *pRoot) {
      //루트 노드를 변경
        *pRoot = GetRightSubTree(pVRoot);
    }

    free(pVRoot);
    return dNode;
}