미분 (Derivative)
🤔미분이란
단어 자체는 작을 미(微)와 나눌 분(分), 즉 “작게 나눈다”라는 의미다.
📕미분 공식
f(x)′=Δxf(x+Δx)−f(x) , Δx→0
다음과 같은 미분 공식을 사용한다.
하지만 실제로 0으로 나눌 수 없기 때문에 0에 근사한 값을 사용하게 된다.
2Δxf(x+Δx)−f(x−Δx)
한편 numerical method 에서는 조금 더 정확한 값을 측정하기 위해 위의 식을
사용하기도 한다.
f(x) = 상수 → f′(x) = 0
f′(x)가 상수 인 경우에는 x를 아무리 늘리거나 줄여도 늘 같은 숫자이기 때문에 변화가 없다.
즉 변화율이 0이기 때문에 미분계수도 0이다.
📘power rule
❗️power rule 적용 기본식
f(x)=axn → f′(x)=anx(n−1)
다음과 같은 식을 적용한다.
✅예시
f(x)=3x4+10
먼저 4승에서 하나를 내려보내서 앞에 있는 3과 곱해준다. (10은 상수이기 때문에
미분을 하면 0이 된다.)
f′(x)=(4∗3)x4
이후에는 4승에서 1을 빼준다.
f′(x)=(4∗3)x4−1
최종 f(x)의 도함수
f′(x)=12x3
x = 2일 때 f'(x)
f′(2)=96
깨봉수학 미분 3편에서 power rule을 상당히 쉽게 설명해주고 있다.
깨봉수학 유튜브 미분 3편 : 3차원 미분
📒chain rule
함수의 함수를 미분하기 위해 사용하는 방식이다.
합성함수라고 부르기도 한다.
양파까기라고 생각하면 이해하기 좀더 쉽다!
❗️chain rule 적용 기본식
F(x)=f(g(x))
F′(x) → f′((g(x))⋅g′(x)
✅예시
F(x)=(2x3+7)6 를 x 에 대해 미분하려는 경우
f(x)=x6,g(x)=2x3+7로 설정
F′(x)=6(2x3+7)5⋅6x2
📗지수 함수
지수함수의 미분은 지수 함수이다.
❗️지수함수의 미분 기본 공식
f(x)=ex → f′(x)=ex
지수 함수의 미분 증명 <출처 MATH FACTORY>
📙편미분
편미분은 다변수 함수의 특정 변수를 제외한 나머지 변수를 상수로 간주하여
미분하는 것이다.
❗️편미분 기본 공식
f(x,y)=x2+2xy+y2
∂x∂f(x,y)=∂x∂(x2+2xy+y2)=2x+2y
y 를 상수로 취급하고 x 를 기준으로 미분하거나 x 를 상수로 취급하고 y 를
기준으로 미분하는 것이 편미분이다.
✅예시
f(x,y)=x2+4xy+9y2라는 함수의 편미분
1. x에 대해 편미분
∂x∂f(x,y) = 2x+4y
2. y에 대해 편미분
∂y∂f(x,y) = 4x+18y
🔖함수란?
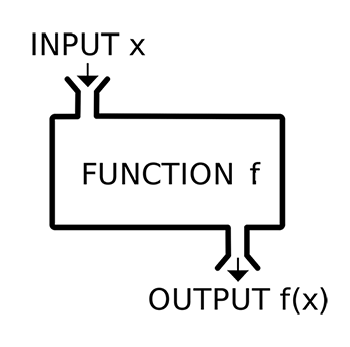
함수는 간단하게 x를 넣으면 f(x)라는 결과값을 내보내주는 기계이다.
간단하게 표현하면 자판기에 돈을 넣고 원하는 음료를 뽑는 것으로 예를 들을 수 있다.
🔖단순선형 모델
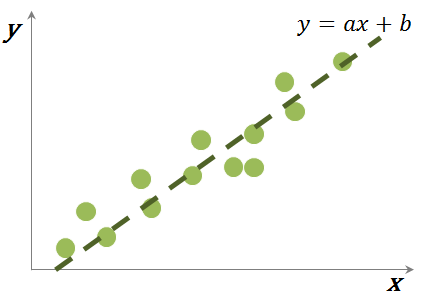
x라는 입력을 주었을 때 y값을 예측하는 단순 선형모델 식
y^=ax+b
a= 회귀계수 b=y 의 절편