[lv.3] 섬 연결하기

https://school.programmers.co.kr/learn/courses/30/lessons/42861

• 문제
  
  

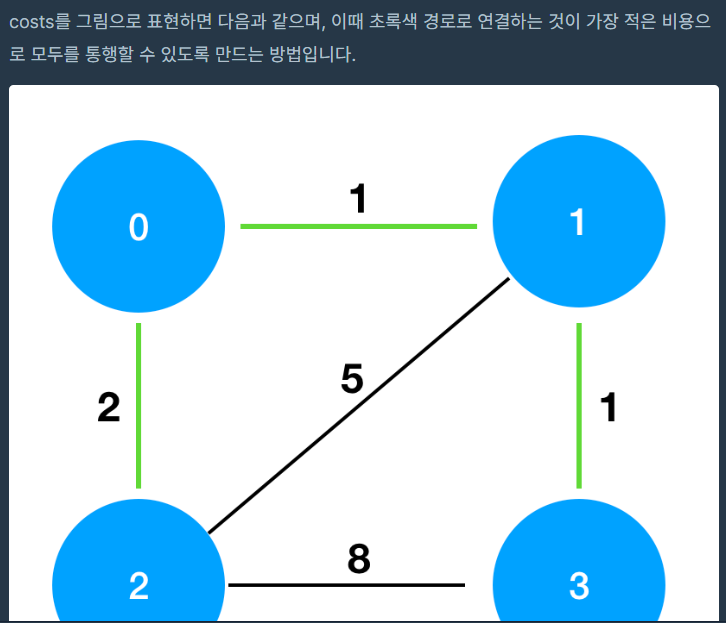
• 풀이
  MST, 최소 신장 트리 문제이다.
  즉, 이 문제를 풀기 위해서는 위의 알고리즘이 필요한데 설명은 나중에 하겠다.
  1) 인덱스의 부모를 표시하는 parent 배열을 만들고 처음엔 인덱스의 부모가 자신이라고 한다.
  parent[] -> 0 1 2 3
  2) cost를 길이순으로 정렬한다.
  Arrays.sort(costs, (o1, o2) -> Integer.compare(o1[2], o2[2]));
[[0,1,1],[1,3,1],[0,2,2],[1,2,5],[2,3,8]]
  이런식으로 될 것이다.
  3) cost[i][0], cost[i][1]을 서로 find, 부모를 찾아 서로 같지 않은 경우에 둘을 union한다.
  4) answer에 union한 두 노드의 거리를 합한다.

• 유니온 파인드
  1) 유니온 : 노드 a와 b의 부모를 찾는다. 이후 parent[큰값]에 작은값을 넣는다.
  2) 파인드 : 노드 a의 부모 parent[a]를 찾을 때까지 find(parent[a])를 재귀한다.

public void union(int a, int b){
    a = find(a);
    b = find(b);
    if(a>b) parent[a] = b;
    else parent[b] = a;
}
public int find(int a){
    if(parent[a]==a) return a;
    else return find(parent[a]);
}

• 최소 신장 트리 : 크루스칼 알고리즘
  https://sskl660.tistory.com/72 이분의 설명을 토대로 하였다.
  1) graph를 간선 오름차순으로 정렬한다.
  2) 이후 계속 union(노드1, 노드2)를 돌려 최단 거리 및 parent를 갱신
  
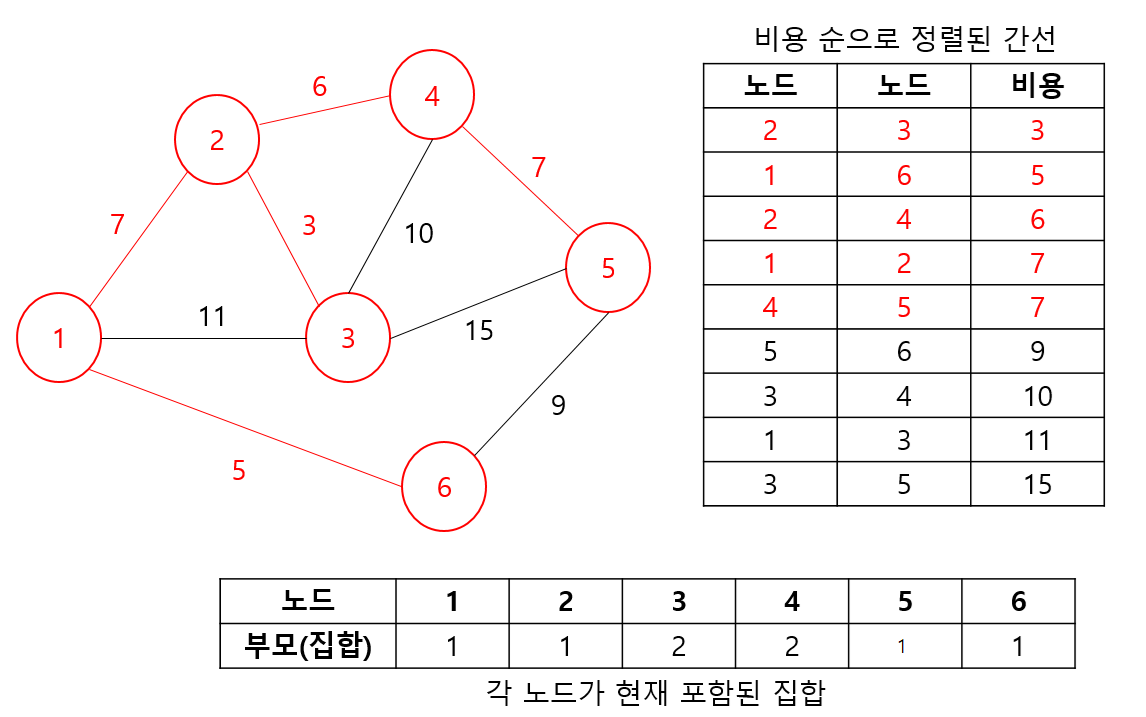
  3) 만약, find(노드1) == find(노드2)일 경우 둘의 parent가 같다는 뜻 -> 노드 연결 시 사이클 발생 -> 스킵
  

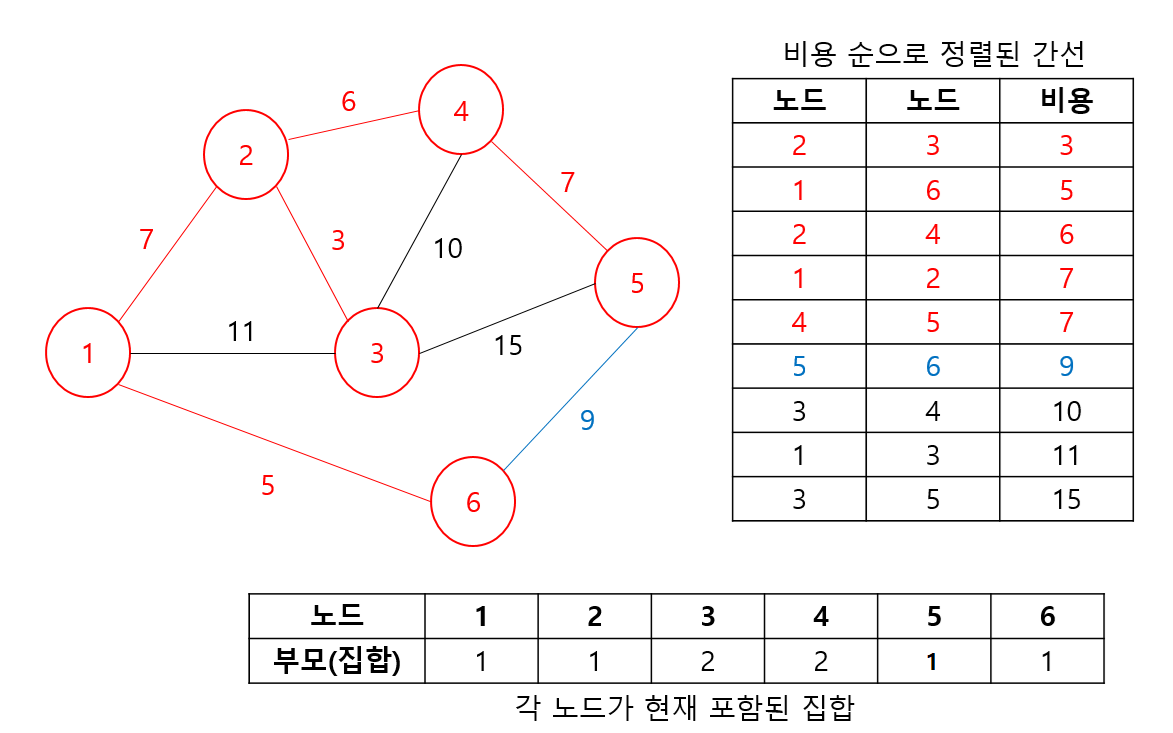
Arrays.sort(costs, (o1, o2) -> Integer.compare(o1[2], o2[2]));
parent = new int[n];
for(int i=0; i<n; i++){
    parent[i] = i;
}
for(int i=0; i<costs.length; i++){
    if(find(costs[i][0]) != find(costs[i][1])){
        union(costs[i][0], costs[i][1]);
        answer += costs[i][2];
        continue;
    }
}

• 코드

import java.util.*;

class Solution {
    static int[] parent;
    public int solution(int n, int[][] costs) {
        int answer = 0;
        Arrays.sort(costs, (o1, o2) -> Integer.compare(o1[2], o2[2]));
        parent = new int[n];
        for(int i=0; i<n; i++){
            parent[i] = i;
        }
        for(int i=0; i<costs.length; i++){
            if(find(costs[i][0]) != find(costs[i][1])){
                union(costs[i][0], costs[i][1]);
                answer += costs[i][2];
                continue;
            }
        }
        return answer;
    }
    public void union(int a, int b){
        a = find(a);
        b = find(b);
        if(a>b) parent[a] = b;
        else parent[b] = a;
    }
    public int find(int a){
        if(parent[a]==a) return a;
        else return find(parent[a]);
    }
}