[자료구조] Tree traversal (Inorder, Preorder, Postorder)

이진트리의 성질

최대 노드 수
(1) 이지트리의 레벨 i에서의 최대 노드 수 : $2^{i-1}$ (i≥1)
(2) 깊이가 k인 이진트리의 최대 노드 수: $2^k-1$ (k≥1)

⇒ $\Sigma_{i=1}^k$ (레벨 i의 최대 노드 수 ) = $\Sigma_{i=1}^k 2^{i-1} = 2^k-1$ (수식 기억할 것)

리프 노드 수와 차수가 2인 노드 수와의 관계
공백이 아닌 모든 이진 트리 T에 대하여 $n_0$ : 리프 노드 수 , $n_2$ : 차수가 2인 노드 수라 하면,
$n_0 = n_2 + 1$

<증명>

• n = $n_0$ + $n_1$ + $n_2$ // 리프 노드 수+ 차수가 1인 노드 + 차수가 2인 노드 모두 더하면 전체 노드 수가 나온다.

• 루트를 제외한 모든 노드들을 들어오는 가지가 하나씩 있으므로 n = B + 1

• 모든 가지들은 차수가 2 또는 1인 노드에서 뻗어나오므로 B = $n_1$ + 2$n_2$
  (branch 는 차수가 1인 노드에서는 하나가 나오고, 차수가 2인 노드에서는 두개가 나올거니까)
  → 이를 조합해 위 정의의 식이 나온다

포화 이진 트리 Full binary tree
깊이가 k이고, 노드수가 $2^k-1$ (k≥0)인 이진 트리
노드 번호 1, ..., $2^k-1$까지 순차적 부여 가능 ⇒ 빈칸이 있으면 안된다

완전 이진 트리 Complete binary tree
→ 최대한 채우려고 한 이진트리 (포화 이진 트리와 다르다)
: 깊이가 k이고 노드 수가 n인 이진트리
: 각 노드들이 깊이가 k인 포화 이진 트리에서 1부터 n까지 번호를 붙인 노드와 1대 1로 일치한다
n노드 완전 이진트리의 높이 : $\lceil log_2(n+1) \rceil$ (올림)

---

이진 트리의 표현

배열 표현
1차원 배열에 노드를 저장한다
n개의 노드를 가진 완전이진트리가 있으면

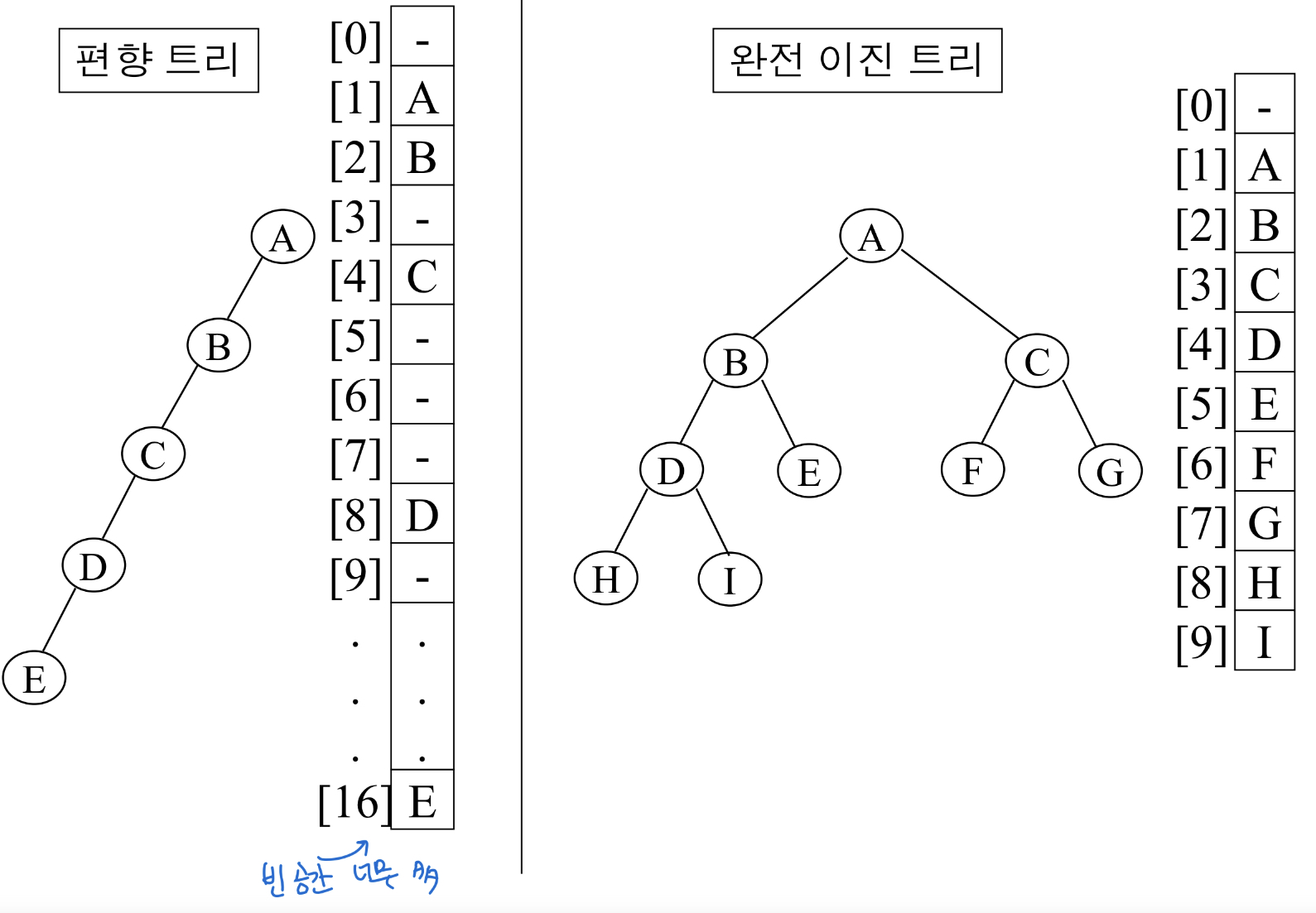
: A의 왼쪽 child는 A의 두 배 / 오른쪽 child는 두 배 + 1
→ 편향 트리는 빈공간이 너무 많지만 완전 이진트리는 빈공간이 없다.
→ 또한 같은 이진트리를 표현하더라도 높이가 적다 → 효율적이라는 의미
→ 그러나 트리의 중간에 노드를 삽입하거나 제거하게 되면 노드 레벨 변경에 따라 많은 노드의 위치가 변해야 함
→ 연결 표현으로 해결 (linked representation)

노드 표현
: 링크드 리스트를 써보면 왼쪽 child에 대한 포인터, 오른쪽 child에 대한 포인터가 있다
→ 노드 구조와 머릿속의 개념적인 구조와 잘 맞는다 !!

: 문제점 - parent를 알기 어렵다 ⇒ parent 필드를 추가해준다

클래스 정의

    template<class T> class Tree; // 전방선언
    template <class T>
    class TreeNode{
    template <T2>
    friend class Tree<T2>;
    private:
        T data;
        TreeNode<T> *leftChild;
        TreeNode<T> *rightChild;
    };
    
    template<class T>
    class Tree{
    public:
    	// 트리 연산들... 
    	...
    private:
    	TreeNode<T> *root;
    }; 

연결 표현의 예

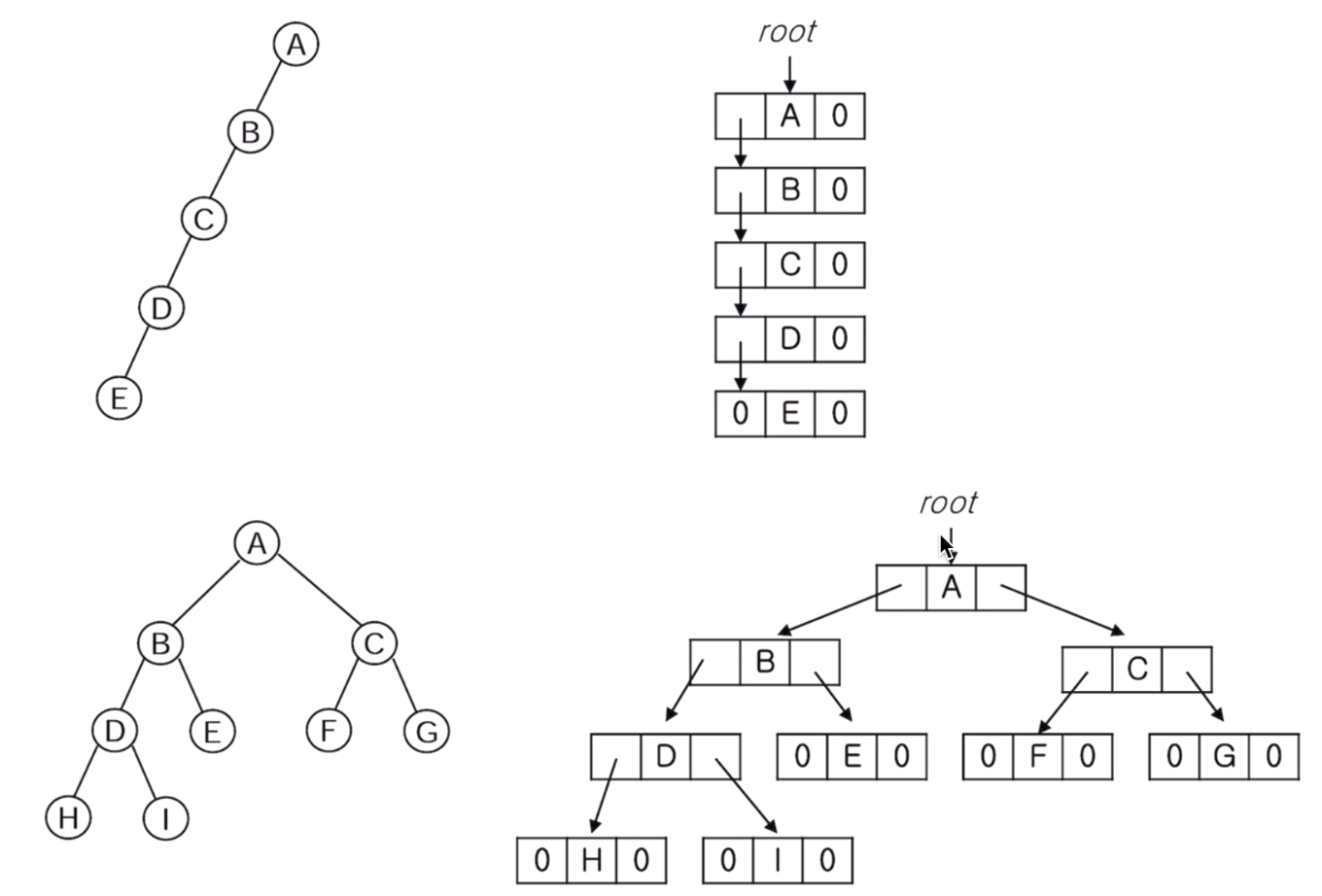
link를 이용해 만들면 → 리프 노드는 어쩔 수 없이 못 써먹는 노드들이 있다

이진 트리 순회와 트리 반복자

트리 순회 (tree traversal)
: 트리에 있는 모든 노드를 한 번씩만 방문하는 트리에서 수행하는 연산 중 하나
: 순회 방법 : LVR, LRV, VLR, VRL, RVL, RLV (L : 왼쪽 이동, V : 노드 방문, R : 오른쪽 방문)

왼쪽을 오른쪽보다 먼저 방문한다 (LR) L과 R에 대한 V의 상대적 위치에 따라
: LVR 중위 순회 inorder traversal
: VLR 전위 순회 preorder traversal
: LRV 후위 순회 postorder traversal

산술식의 이진트리 표현
: Parsing tree (A/BCD+E)

Inorder Traversal (recursive하게)
- 왼쪽 자식 방문 → 루트 방문 → 오른쪽 자식 방문

template<class T>
    void Tree<T>::Inorder(){
        Inorder(root);
    }
    
    template <class T>
    void Tree <T>::Inorder(TreeNode<T> *currentNode){ 
    // Inorder니까 LVR
    
        if (currentNode){ // currentNode가 0이 아니면
            Inorder(currentNode->leftChild);
            // 무조건 왼쪽으로 : 0이 아닌 값이 나올 때까지 recursive하게 계속
    
            Visit(currentNode); //끝나면 현재 노드 출력
            Inorder(currentNode->rightChild); // 그다음 오른쪽으로
        }
    }

Inorder Traversal (non-recursive version)
왼쪽 자식 방문 → 루트 방문 → 오른쪽 자식 방문

• 출력 결과 A / B C D + E

    // 중간단계를 다 저장 하면서 내려갔다가 다시 거꾸로 올라온다
    // 이런 자료구조에는 stack이 필요하다
    
    template<class T>
    void Tree<T>::NonrecInorder(){
        Stack<TreeNode<T> *> s;  // 스택 자료구조가 필요함
        TreeNode<T> *currentNode = root;
        while (1){
            while (currentNode){
                s.Push(currentNode);
                currentNode = currentNode->leftChild;
            } // stack에 넣으면서 쭉 내려간 다음
            
            if (s.IsEmpty()) return; // 스택이 비었으면 리턴 (tree가 empty란 이야기)
            currentNode = s.Top(); s.Pop(); // 스택에서 하나 꺼내서
            Visit(currentNode); // currentNode를 출력한 다음
            currentNode = currentNode->rightChild; // rightChild로 가서 while 루프 반복 
        }
    }

Preorder Traversal
먼저 root를 출력하고 왼쪽, 그다음 오른쪽

• 출력 결과 : +**/ABCDE
• 노드를 먼저 방문하고 왼쪽으로 가서 계속한다. 더 이상 계속할 수 없으면 오른족으로 이동하여 다시 시작하거나, 오른쪽으로 이동하여 순회를 계속할 수 있을 때까지 되돌아간다.

    template<class T>
    void Tree<T>::Preorder(){
        Preorder(root); // root를 가지고 Preorder를 해봐
    }
    
    template<class T>
    void Tree<T>::Preorder(TreeNode<T> *currentNode){ // Preorder 구현
        if (currentNode){
            Visit(currentNode); //일단 currentNode 출력
            Preorder(currentNode->leftChild); // 왼쪽으로 가봐
            Preorder(currentNode->rightChild);
        }
    }
    // prefix notation으로 출력한다

Postorder Traversal

• 왼쪽 자식 방문 → 오른쪽 자식 방문 → 루트 방문
• 출력 결과 AB/CDE+ → postfix notation으로 출력됨

    template<class T>
    void Tree<T>::Postorder(){
        Postorder(root);
    }
    
    template<class T>
    void Tree<T>::Postorder(TreeNode<T> *currentNode){
        if(currentNode){
            Postorder(currentNode->leftChild);
            Postorder(currentNode->rightChile);
            Visit(currentNode);
        }
    }

Level Order Traversal 레벨 순서 순회
앞에 있는 레벨부터 먼저 출력해. 먼저 나오는 걸 먼저 출력해야 하니까 필요한 자료구조 (FIFO) → 큐 사용!

• 루트 방문 → 왼쪽 자식 방문 → 오른쪽 자식 (같은 레벨 상) 방문하되 각 레벨별로 최좌측 노드에서 최우측 노드를 모두 방문한다.
• 출력 결과 : +ED/CAB

    template<class T>
    void Tree<T>::Levelorder(){
        Queue<TreeNode<T> *> q; //큐를 만든다
        TreeNode<T> *currentNode = root; // root부터 시작
        
        while(currentNode){
            Visit(currentNode); // 제일 앞에 있는 노드는 root니까 너 출력
            
            if(currentNode->leftChild) //leftChild가 있으면
                q.Push(currentNode->leftChild); // leftChild를 큐에 넣는다
            
            if(currentNode->rightChild) // rightChild가 있으면
                q.Push(currentNode->leftChild); // 큐에다 넣는다
            
            if(q.IsEmpty()) return; // 비었으면 끝났다는 것
            
            currentNode = q.Front(); // 큐에서 꺼내자
            q.Pop();
        }
    }

Traversal without a Stack 스택없는 순회

• Recursive 호출 시 스택을 사용한다
• 각 노드에 parent필드 추가 : 스택을 사용하지 않아도 루트 노드로 올라갈 수 있음

Threaded binary tree로 표현
: 각 노드마다 두 비트 필요
: leaf의 leafChild 필드와 rightChild 필드를 사용하여 루트로 돌아가는 경로를 유지한다
: The stack of address is stored in the leaf nodes.