[알고리즘] Optimal Binary Search Trees

💫 Optimal Binary Search Trees

---

이진 트리에서 빈도수와 검색 비용을 이용해서, 어떻게 배치하면 검색 비용을 줄일 수 있을지에 대해서 탐색

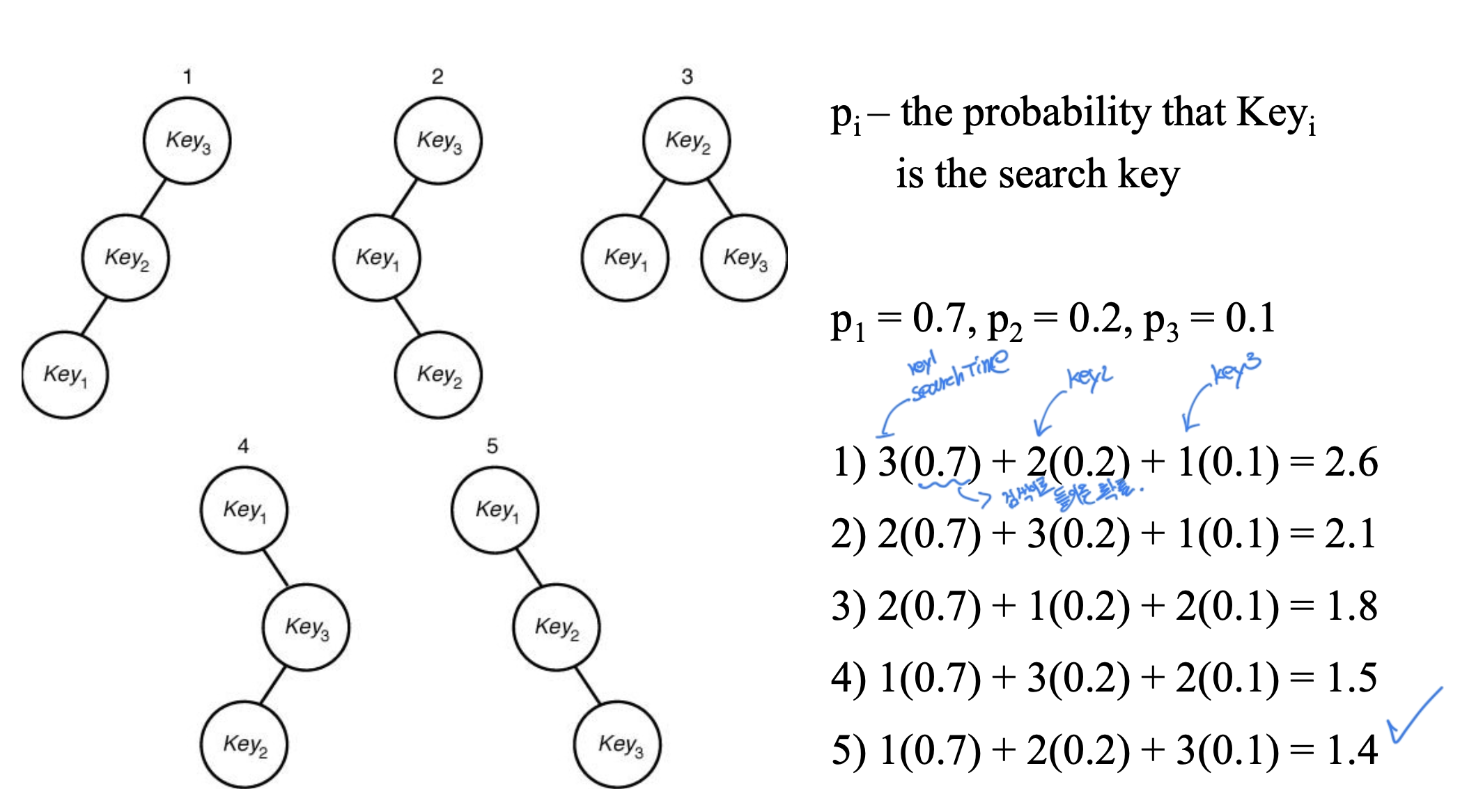
예시를 보면 5번 이진 트리가 가장 탐색 비용이 적은 것을 알 수 있다.

A[][] 행렬은 탐색 비용으로써 위의 식과 같이 계산이 된다. K는 root로 가정한 노드를 가르킨다.

A[i][i]는 key의 확률의 값을 가진다.

📁 수도 코드

void optsearchtree(int n, const float p[], float& minavg, index R[][]) {
   index i, j, k, diagonal;
   float A[1..n+1][0..n];
   for(i=1; i<=n; i++) {
      A[i][i-1] = 0; A[i][i] = p[i]; R[i][i] = i; R[i][i-1] = 0;
   }
   A[n+1][n] = 0; R[n+1][n] = 0;
   for(diagonal=1; diagonal<= n-1; diagonal++)
 		for(i=1; i <= n-diagonal; i++) {
			j = i + diagonal
			A[i][j] = min(A[i][k-1]+A[k+1][j]) + p//(p는  i부터 j까지 확률의 합) 
            //(i<=k<=j)
            R[i][j] = a value of k that gave the minimum;
      	}
      minavg = A[1][n];
}

nodepointer tree(index i, j) {
      index k;
      node_pointer p;
      k = R[i][j];
      if(k==0)
          return NULL;
      else{
          p = new nodetype;
          p -> key = key[k];
          p -> left = tree(i, k-1);
          p -> right = tree(k+1, j);
		  return p; 
	 }

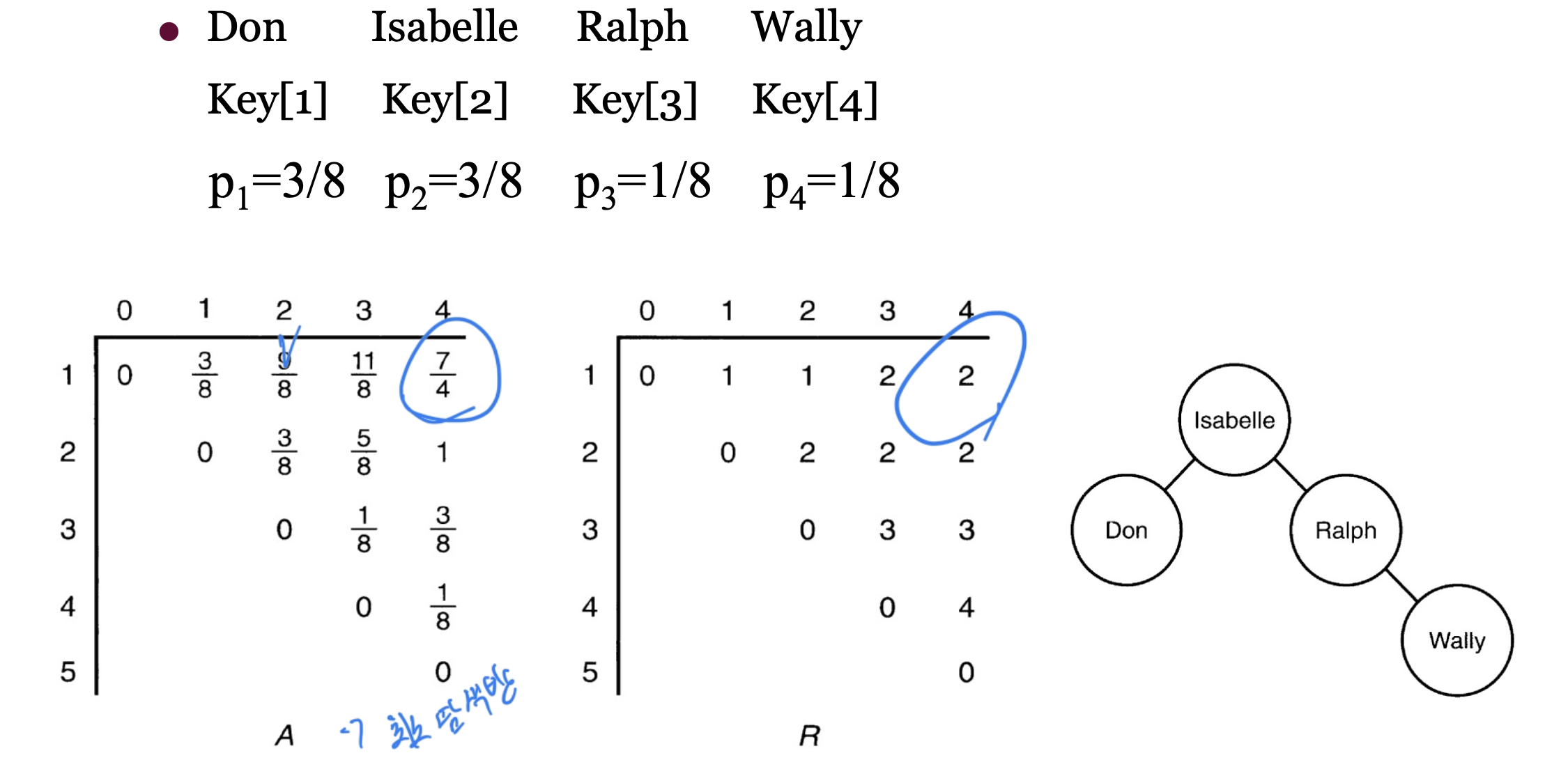
• 알고리즘 적용

$Key[1] = \text{Don}, p_1 = \frac{3}{8} Key[2] = \text{Isabelle}, p_2 = \frac{3}{8} Key[3] = \text{Ralph}, p_3 = \frac{1}{8} Key[4] = \text{Wally}, p_4 = \frac{1}{8}$

단계 1: 두 개의 키 계산

1. A[1][2] :  Key[1] 와  Key[2] 를 포함하는 서브트리.

   • 확률 합:  $p_1 + p_2 = \frac{3}{8} + \frac{3}{8} = \frac{6}{8} .$
   • 루트 후보 :

     • 루트:  Key[1]

       $A[1][2] = A[1][0] + A[2][2] + \frac{6}{8} = 0 + \frac{3}{8} + \frac{6}{8} = \frac{9}{8}$
       

     • 루트:  Key[2]

       $A[1][2] = A[1][1] + A[3][2] + \frac{6}{8} = \frac{3}{8} + 0 + \frac{6}{8} = \frac{9}{8}$

       탐색 비용이기 때문에 값이 적을 수록 좋음

   결과 둘다 가능.

   이런 방식으로 표를 채워 나간다.

📁 시간 복잡도

시간 복잡도 : $n^2$