멀쩡한 사각형
문제 설명
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.
제한사항
W, H : 1억 이하의 자연수
입출력 예
W H result
8 12 80
입출력 예 설명
입출력 예 #1
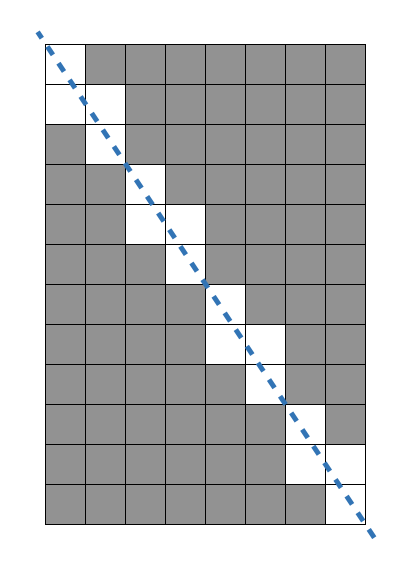
가로가 8, 세로가 12인 직사각형을 대각선 방향으로 자르면 총 16개 정사각형을 사용할 수 없게 됩니다. 원래 직사각형에서는 96개의 정사각형을 만들 수 있었으므로, 96 - 16 = 80 을 반환합니다.
https://programmers.co.kr/learn/courses/30/lessons/62048?language=python3#
📋 풀이(시간초과)
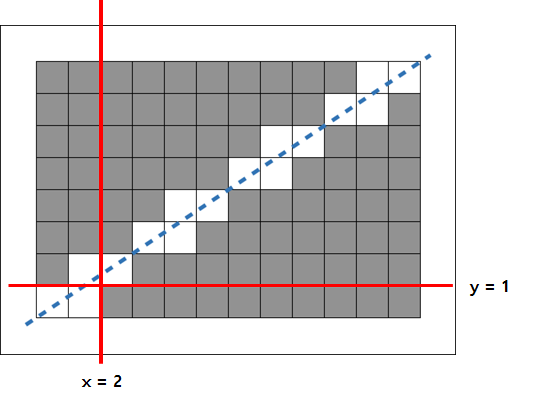
대각선이 좌표 평면의 기울기로 보이도록 회전하였다. y가 1부터 height까지 맞닿는 x좌표를 올림하여 그 이후의 칸을 더하였다.(width - x) 대각선을 기준으로 좌우대칭이므로 절반만 구하고 구한 값의 2배를 출력하였다. 시간을 조금이라도 줄이고자 width와 height 중에서 더 짧은 길이를 height로 지정하였으나 시간초과가 발생하였다. width와 height의 길이가 비슷하고 그 크기가 엄청나게 큰 경우인듯하다.
import math
def solution(width, height):
half_count = 0
if height > width:
width, height = height, width
a = height / width # 기울기
for y in range(1, height):
x = math.ceil(y / a)
half_count += width - x
return half_count * 2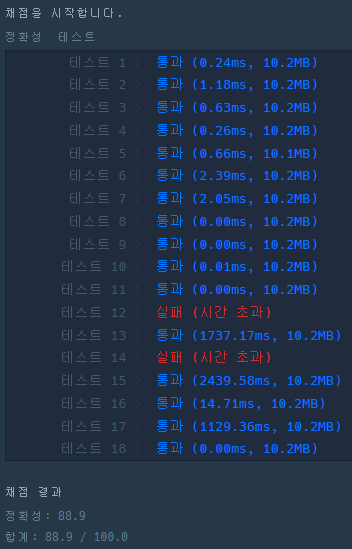
📋 다른 사람 풀이
https://leedakyeong.tistory.com/entry/%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%A8%B8%EC%8A%A4-%EB%A9%80%EC%A9%A1%ED%95%9C-%EC%82%AC%EA%B0%81%ED%98%95-in-python
width와 height이 커질수록 대각선을 지나는 주변 패턴이 동일하며 그것이 최대공약수의 수만큼 반복된다는 것을 이용하여 공식을 만들어냈다. 자세한건 블로그를 참고하길 바란다.
import math
def solution(w,h):
return w * h - (w + h - math.gcd(w, h))대각선 주위로 동일한 패턴을 보이는 것은 알았지만 그것이 어떠한 기준을 가지고 반복되는지를 파악하지 못했다. 또 시간초과가 발생했을 때 다른 관점에서 보는 것이 아닌 코드 내의 문제점을 찾기에 급급했다. 대다수 시간초과가 발생하면 방식이 틀린 것은 아니나 완전히 다른 방식으로 풀어야하는 문제니 주의하자.
20211026
이전 블로그에서 다른 문제 찾다가 예전에 풀었다 실패한 코드를 발견했다. 그때보다 코드 길이도 줄었고 테스트케이스도 조금 더 성공했다. 뿌듯하다 희희😊
