[TIL] 10월 22일: 백준 4948번

에라토스테네스의 체를 적용하지 않고 소수를 구했는데 시간 초과가 떴다.
그래서 에라토스테네스의 체를 적용했다. 에라토스테네스의 체를 적용해 성공은 했는데 200ms만 더 늦었으면 시간 초과할 뻔 했다.

에라토스테네스의 체

고대 그리스의 수학자 에라토스테네스가 만들어 낸 소수를 찾는 방법이다. 이 방법은 마치 체로 치듯이 수를 걸러낸다고 해서 에라토스테네스의 체라고 부른다.
특정 범위가 주어지고 그 범위 내의 모든 소수를 찾아야 하는 경우 아직까지 소수들 간의 연관성(소수를 생성할 수 있는 공식)이 나오지 않았으므로 에라토스테네스의 체보다 빠른 방법이 없다. 프로그래밍에도 수학적 지식이 필요하다는 걸 일깨워주는 좋은 예시다.

방법

예시: 1~100 숫자 중 소수 찾기

1. 1부터 100까지 숫자를 쭉 나열한다.
   

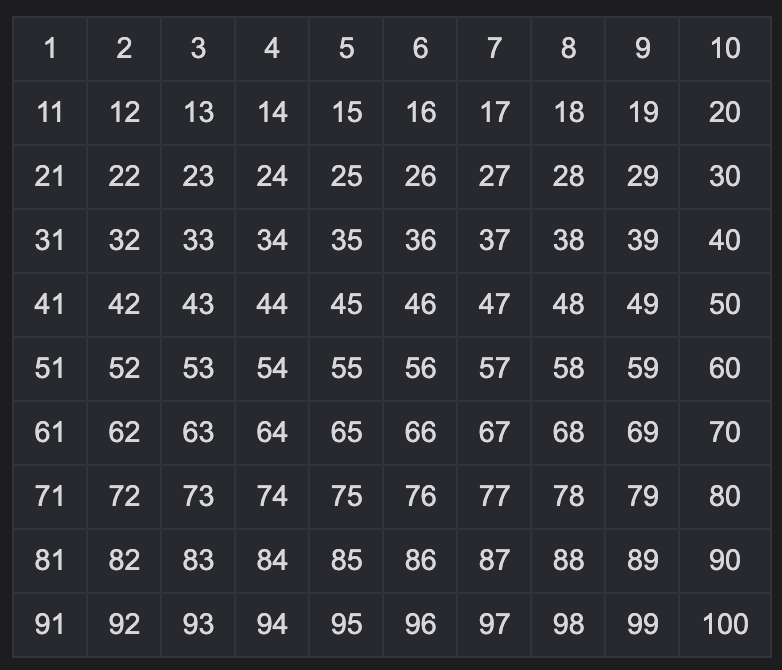
2. 소수도, 합성수도 아닌 유일한 자연수 1을 제거한다.
   

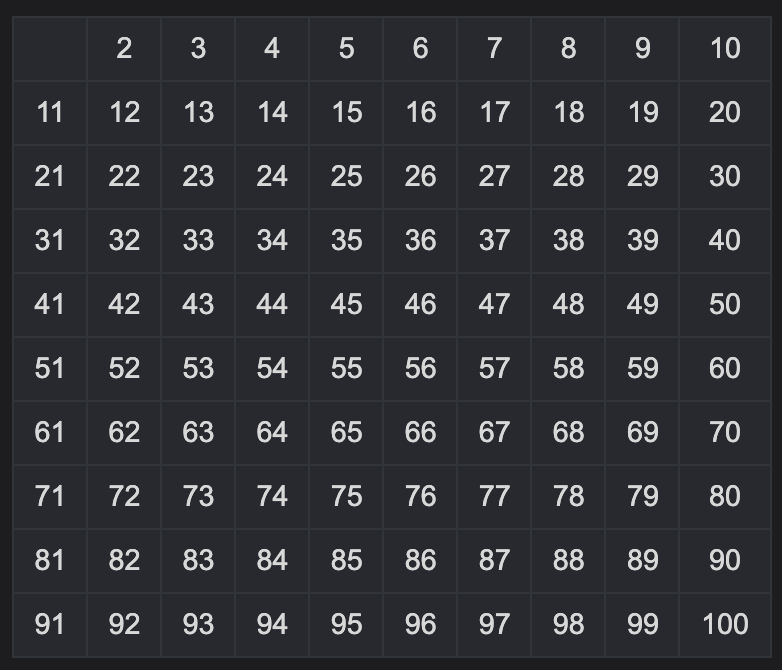
3. 2를 제외한 2의 배수를 제거한다
   

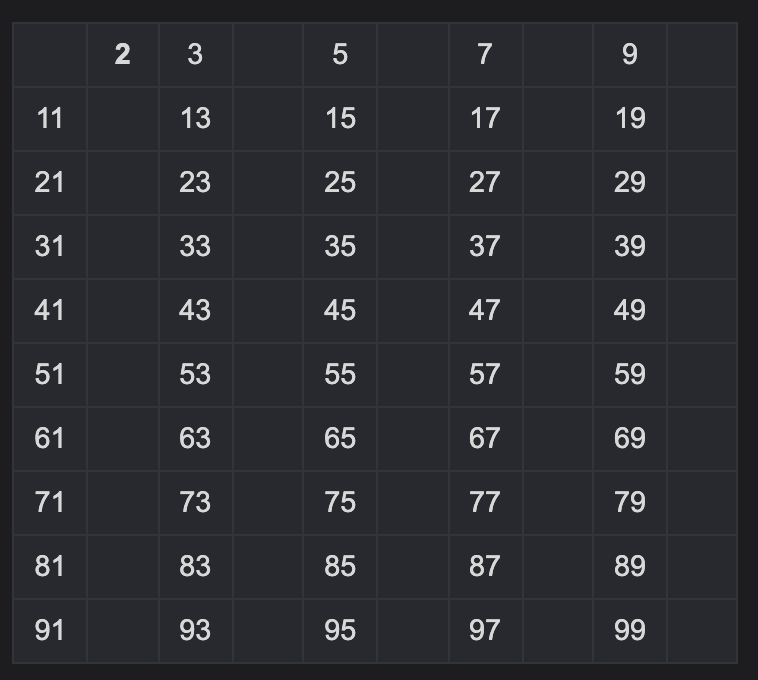
4. 3을 제외한 3의 배수를 제거한다.
   

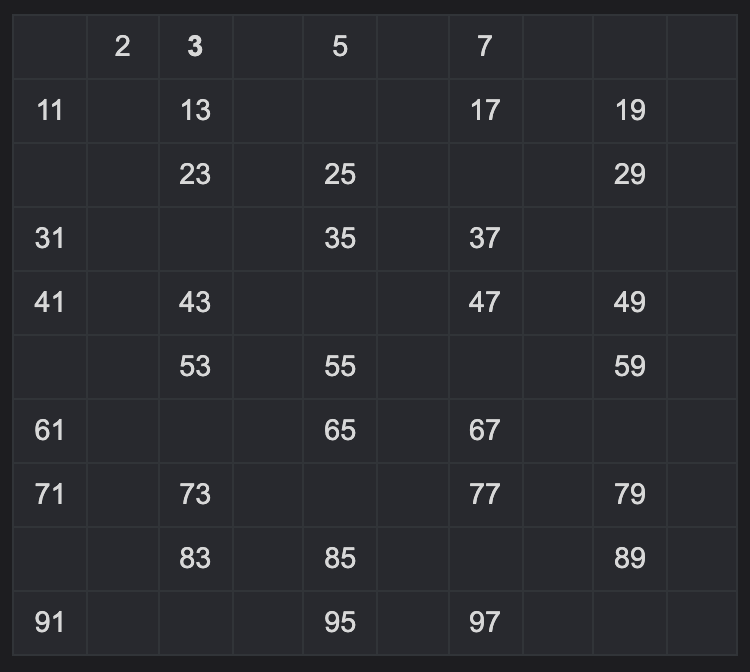
5. 4의 배수는 지울 필요 없다.(2의 배수에서 이미 지워졌다.)
   그러면 2, 3 다음으로 남아있는 가장 작은 소수, 즉 5를 제외한 5의 배수를 제거해야 한다.
   

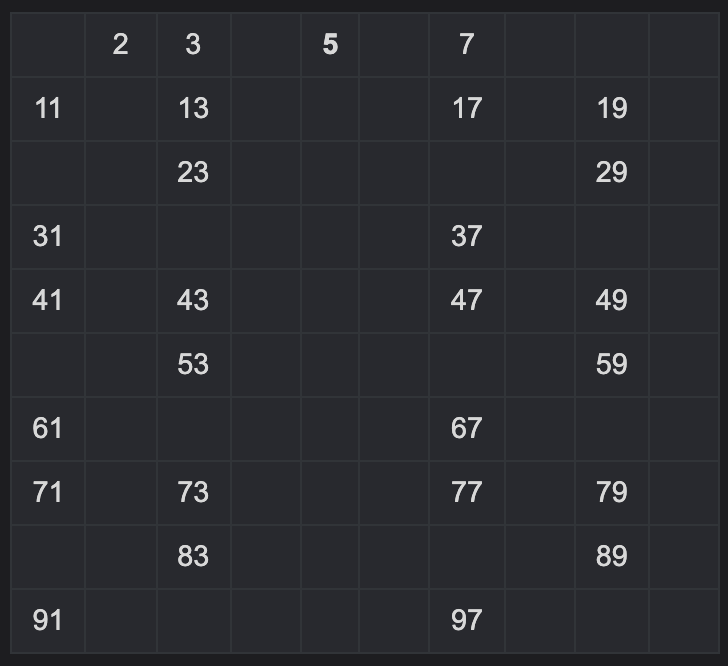
6. 그리고 마지막으로 7을 제외한 7의 배수까지 제거한다.
   

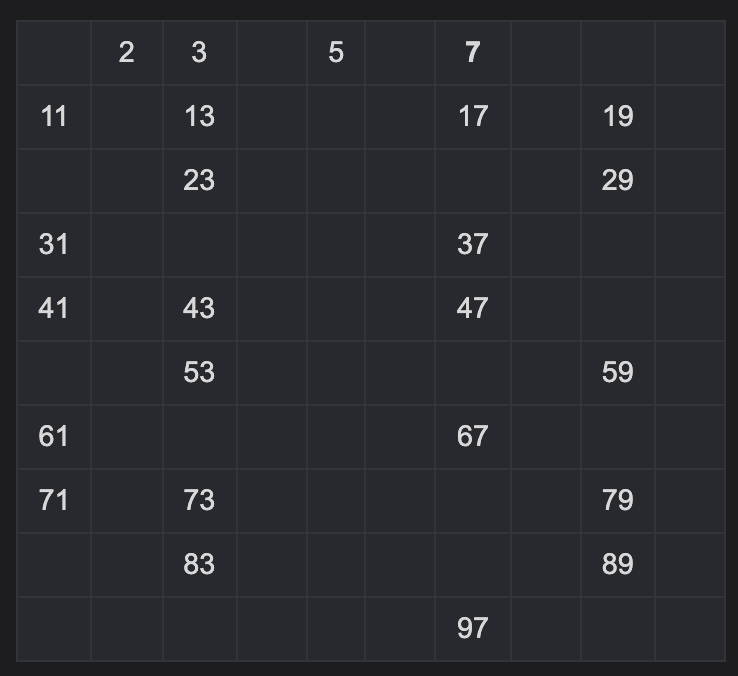
7. 8의 배수는 지울 필요 없다.(2의 배수에서 이미 지워졌다.) 9의 배수도 지울 필요 없다.(3의 배수에서 이미 지워졌다.) 10의 배수도 지울 필요 없다.(2의 배수에서 이미 지워졌다.) 그리고 11 이상의 소수들의 배수부터는 11 > 루트 100(100의 제곱근) 이기 때문에 역시 지울 필요 없다.

에라토스테네스의 체를 이용해 1 ~ n까지의 소수를 알고 싶다면, n까지 모든 수의 배수를 다 나눠 볼 필요는 없다. 만약 어떤 수 m = ab라면 a와 b 중 적어도 하나는 루트 n이하다. 즉, n보다 작은 합성수 m은 루트 n보다 작은 수의 배수만 체크해도 전부 지워진다는 의미이므로, 루트 n 이하의 수의 배수만 지우면 된다.

참고

---

처음에 제출했던 코드(에라토스테네스의 체 미적용) - 시간 초과

from sys import stdin


def sosu(num):
    for i in range(2, int(num ** 0.5) + 1):
        if num % i == 0:
            return False
    return True


while True:
    n = int(stdin.readline())
    count = 0
    if n == 0:
        break
    for j in range(n + 1, 2 * n + 1):
        if sosu(j):
            count += 1
    print(count)

문제에서 정해진 범위의 수 n에 대하여 미리 소수를 구해 리스트에 저장해 이를 이용(에라토스테네스의 체 미적용) - 1324ms

from sys import stdin


def check_prime(num):
    for i in range(2, int(num ** 0.5) + 1):
        if num % i == 0:
            return False
    return True


repo = []

for j in range(2, 246913):  # 1 <= n <= 123456
    if check_prime(j):
        repo.append(j)

while True:
    n = int(stdin.readline())
    count = 0

    if n == 0:
        break
    for k in repo:
        if n < k <= n * 2:
            count += 1
    print(count)

에라토스테네스의 체 적용 - 1844ms

from sys import stdin


# num 이하의 소수 구하기
def check_prime(num):
    sieve = [True] * (num + 1)

    for i in range(2, int(num ** 0.5) + 1):
        if sieve[i]:
            for j in range(i + i, num + 1, i):
                sieve[j] = False

    return [i for i in range(2, num + 1) if sieve[i]]


while True:
    n = int(stdin.readline())
    result = []
    count = 0
    if n == 0:
        break
    for k in check_prime(n * 2 + 1):
        if n < k <= n * 2:
            result.append(k)
    print(len(result))

문제에서 정해진 범위의 수 n에 대하여 미리 소수를 구해 리스트에 저장해 이를 이용(에라토스테네스의 체 적용) - 856ms

from sys import stdin


# num 이하의 소수 구하기
def check_prime(num):
    sieve = [True] * (num + 1)

    for i in range(2, int(num ** 0.5) + 1):
        if sieve[i]:
            for j in range(i + i, num + 1, i):
                sieve[j] = False

    return [i for i in range(2, num + 1) if sieve[i]]


repo = check_prime(123456 * 2)

while True:
    n = int(stdin.readline())
    count = 0
    if n == 0:
        break
    for k in repo:
        if n < k <= n * 2:
            count += 1
    print(count)