
2020년에 획기적인 확산 모델 논문이 나왔다. 이름하여 DDPM! (denoising diffusion probablistic model의 줄임말)
최근 생성 모델링에서 핫한(?) diffusion 모델의 주요 논문이다.
이번 포스팅에서 diffision 모델이 무엇이고 그 기본 원리와 이를 작동하게 하기 위한 모델의 구성 요소에 대해 알아보자!
1. Denoising diffusion model
Denoising diffusion model을 직영하면 잡음 제거 확산 모델이다. 이 모델의 핵심 아이디어는 다음과 같다.
연속해서(여러 번의 과정으로) 매우 조금씩 이미지에서 잡음을 제거하도록 모델을 훈련시키는 것이다.
그렇게 되면 이론적으로 완전히 랜덤한 잡음에서 훈련 세트의 이미지와 같은 이미지를 얻을 수 있다.
Denoising diffision 모델 학습에는 크게 두 가지의 과정이 필요하다.
1. 정방향 확산 과정 (diffusion process)
2. 역방향 확산 과정 (denoising process)
이에 대해 조금 더 자세히 알아보자.
2. 정방향 확산 과정 (diffusion process)
Forward process라고도 불리는 정방향 확산 과정은 원본 이미지에 noise를 점진적으로 적용하는 과정이다.
이때의 noise는 가우시안 노이즈로 평균이 0이고 분산이 1인 노이즈이다.
원본 이미지에 가우시안 노이즈를 조금씩 1000번 적용했다고 해보자.
그러면 1000번째로 적용한 이미지는 가우시안 노이즈와 거의 동일할 것이다.
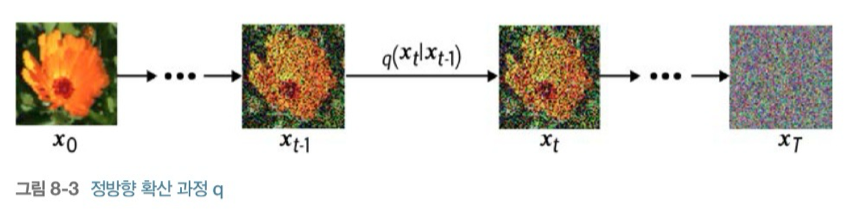
이를 식 로 표현한다.
에서 가우시안 잡음(소량)을 추가한 의 분포라고 볼 수 있을 것이다.
이를 수학적으로 표현하면 다음과 같다.
갑자기 가 나와서 헷갈릴 수 있지만 하나하나 보면 이해하기 쉽다.
우선 위에서 언급한 것처럼 정방향 패스에서는 원본 이미지에 소량의 가우시안 노이즈를 넣어 완벽한 가우시안 노이즈 분포를 만들어 내고 싶다.
따라서 가 될 것이다.
여기서 a,b는 스케일 값 (얼만큼의 이전 이미지를 포함할지(a), 가우시안 노이즈를 포함할지(b)) 이다.
따라서 가우시안 노이즈 를 소량 적용할 가 적용되는 것이다.
그렇다면 왜 와 를 스케일 값으로 만들었을까? (여기서 는 상수이다.)
결론적으로는 이런 식을 통해 T가 클 때,는 표준 가우스 분포에 가깝다는 식이 도출되기 때문이다.
유도하기 위해서는 와
의 성질(공식)을 알아야 한다.
을 평균이 0 분산이 1로 하였기 때문에 위의 첫 번째 공식에 따라
의 분산은 가 되고,
의 분산은 가 된다.
이 둘을 더하게 되면 (= 분포 유도)
평균이 0이고 분산이 1 ( = 1)인 또 다른 새로운 분포를 얻게 되는 것이다.
즉 원본 이미지에 소량의 가우시안 분포를 추가하면서 항상 를 표준 가우스 분포와 거의 동일하다는 게 만들겠다는 아이디어이다.
다행히도 q를 t번 적용하지 않고 원본 이미지에서 로 한 번에 갈 수 있다.
(위의 식에서 대입만 하면 도출되는 있는 식이지만 직접 전개하기에 너무 길고 복잡하기 때문에 생략)
따라서 정방향 확산 방향의 과정 q는 아래의 식과 같이 표현할 수 있다.

라고 가정하면
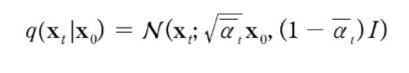
이 식이 만족한다.
2-1 Diffusion schedule
이렇게 되면 에 대해서도 궁금할 것이다.
앞서 말한 것처럼 는 어떠한 상수인데 이를 어떻게 정해야 하는 것일까?
이를 확산 스케줄 혹은 베타 스케줄이라고 부른다.
각 타인 스텝 t에 따라 다른 값을 선택할 수 있다.
값이 t에 따라 변하는 방식을 확산 스케줄이라고 부른다.
다양한 확산 스케줄이 있다. 아래의 그림에서처럼 linear, sigmoid, quadratic 한 스케줄링뿐만 아니라 cosine(+offset cosine) 스케줄링까지 사용하여 t번의 확산을 하게 된다.

위의 그림에서 알 수 있듯이 각 스케줄링에 따라 잡음의 추가 과정에서 얼마나 바뀌는지 알 수 있다.
논문에서는 선형적인 스케줄링 방법을 사용했으나(0.0001 ~ 0.02 범위에서 선형적으로 증가) 시그모이드나 코사인 스케줄링을 사용하면 보다 값이 느리게 상승하게 되므로 더욱 점진적인 노이즈 추가가 가능해진다.
이는 훈련의 효율성과 생성 품질을 향상하는 역할을 한다.
3.역방향 확산 과정(reverse process)
정방향 확산 과정을 통해 우리는 원본 이미지에 잡음을 점진적으로 추가했다.
정방향 확산 과정에서는 학습할 파라미터가 없다. 실제로 베타 스케줄링은 학습 파라미터가 아니다.
반면 역방향 확산 과정에서는 정방향 확산 과정을 되돌릴 수 있는 신경망을 구축한다.
의 분포를 근사화하는 신경망을 구축하는 것이다.
이 신경망은 랜덤한 잡음(가우시안 노이즈)을 샘플링하고 역방향 확산 과정을 '여러 번' 적용하여 새로운 이미지를 생성하게 한다.
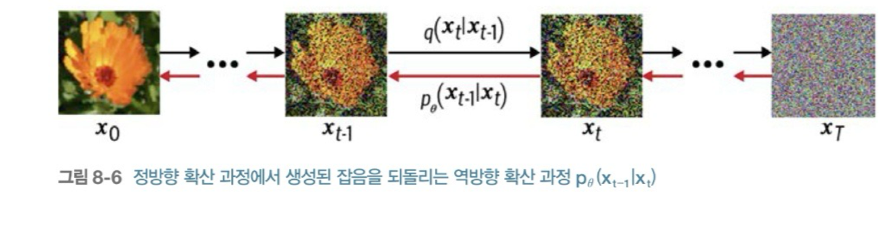
역방향 확산 신경망은 어떠한 타임 스텝 t에서 원본 이미지 로부터 추가된 잡음 을 예측한다.
(t 시점의 이미지는 원본 이미지에 얼만큼의 잡음이 추가되어 있는 가를 예측)
해당 신경망의 학습을 위해서는 원본 이미지에 정방향 확산을 적용시켜 의 이미지와 잡음 비율 를 신경망에 전달하여 을 예측하게 되는 것이다.
따라서 loss는 예측한 와 실제 의 오차와 관련된 loss function을 쓰면 된다.
여기서는 제곱 오차를 사용했다.
또한 잡음 제거 모델로 Unet을 사용했다.
Unet의 구조는 다음과 같다.
(조금 더 자세한 Unet 구조 설명은 논문 리뷰를 통해 하겠다.)
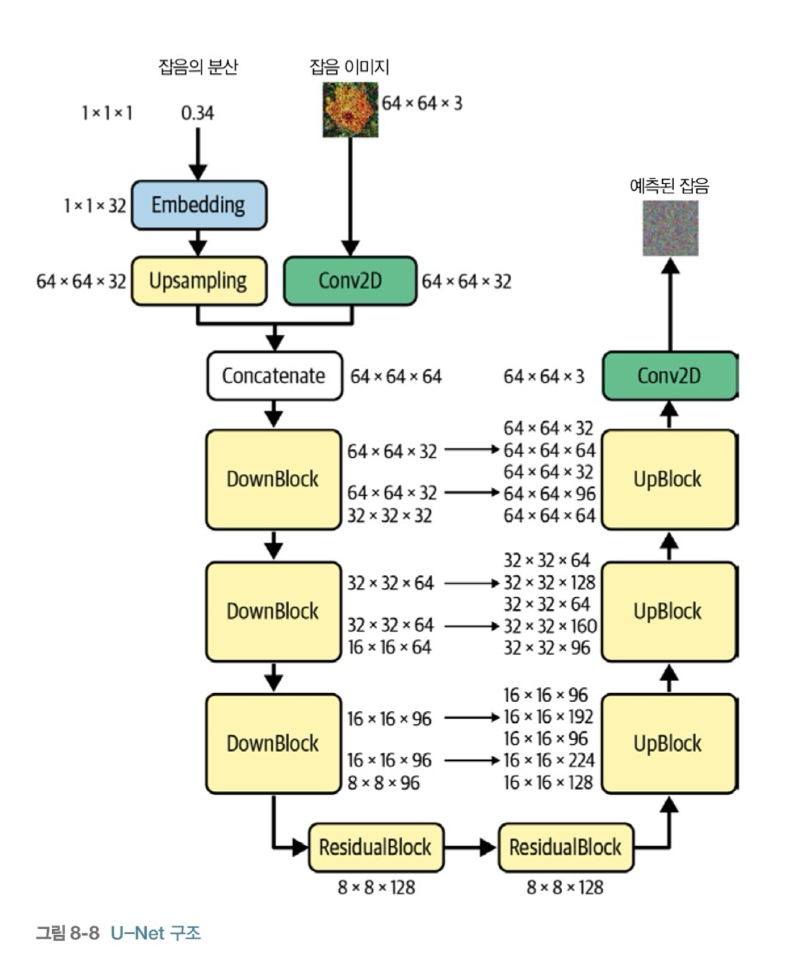
Unet은 의 분산과 이미지를 입력으로 받아 같은 해상도(size)의 을 출력한다.
3-1 모델에서 샘플링하기
Unet이 학습을 잘해서 입력에 대한 을 잘 예측하면 우리는 비로소 훈련 이미지 세트로부터 이미지를 샘플링할 수 있다.
먼저 모델이 예측한 를 사용하여 를 추정한다.
그 후 추정한 에서 를 t-1까지만 재적용하여 새로운 을 추정한다.
이 과정을 반복하면 조금씩 점진적으로 에 대한 추정치로 돌아갈 수 있다.
아래의 그림을 참고하면 이해하기 쉽다.
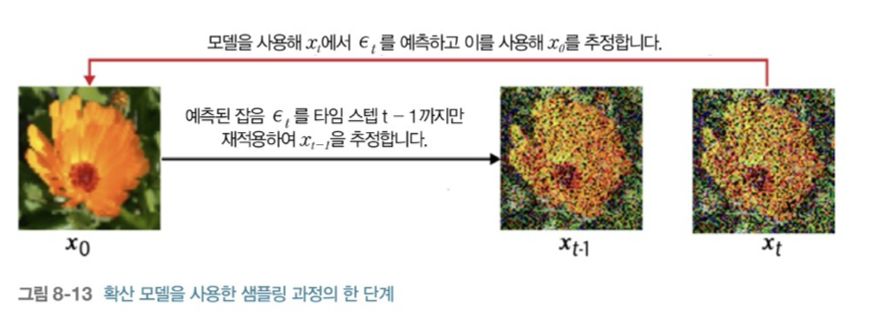
여기서 재적용할 단계는 타임스텝 t(정방향 확산 단계에서 정함)와 같을 필요가 없다고 한다.
다만 알아둬야 하는 것은 단계가 많아질 수록 이미지 생성 품질이 높아진다는 것과 이미지 생성에 대한 시간이 선형적으로 증가한다는 것이다.

실제 훈련과정의 각 에폭에서 샘플링한 이미지를 보면 에폭이 증가할수록 훈련이 잘 되어 잡음(노이즈)을 잘 예측하고 이를 denoising 함으로써 보다 그럴싸한 이미지가 샘플링되는 것을 볼 수 있다.
이번 장에 대한 실습 코드는 깃허브에 올려 참고하면 좋을 것 같다.
8장 실습 code
reference
[1]diffusion 설명 영상, http://%20https//www.youtube.com/watch?v=jaPPALsUZo8&t=463s
