DFS와 BFS

• 대표적인 그래프 탐색 알고리즘
  
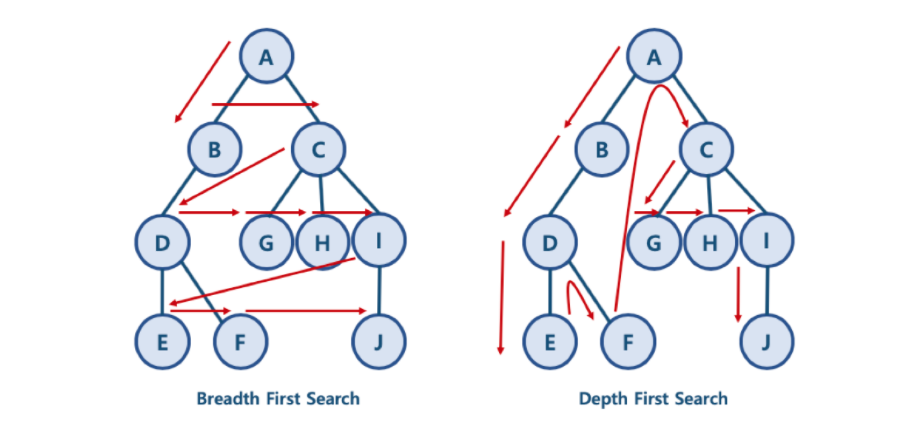
• DFS 방식: A - B - D - E - F - C - G - H - I - J
  - 한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와서 다른 형제들의 자식을 타고 내려가며 순화함
• BFS 방식: A - B - C - D - G - H - I - E - F - J
  - 한 단계씩 내려가면서, 해당 노드와 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 순회함

---

DFS

Ideas

• 깊이 우선 탐색 (Depth First Search): 정점들의 자식들을 먼저 탐색
• 특정 노드에서 시작, 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽히 탐색하는 방법
• 재귀 사용

How To

1. 시작 노드(v)를 먼저 방문, 방문처리를 해준다.
2. 그래프 내 인자를 확인하며 방문하지 않은 경우 재귀를 돌린다.

Code

graph = [
    [],
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]
N = len(graph)
visited = [False] * N


# DFS, 재귀 사용
def dfs(graph, v, visited):  # 시작점 v
    visited[v] = True  # 방문처리
    print(v, end=' ')

    for i in graph[v]:  # 다음으로 방문할 노드 중
        if visited[i] == 0:  # 방문하지 않았다면
            dfs(graph, i, visited)  # 다음 점 i에서 dfs
dfs(graph, 1, visited)
# 1 2 7 6 8 3 4 5

Analysis

• 노드의 수 = V, 간선 수 = E일 때 DFS의 시간복잡도: O(V+E)
• 현재 경로상의 노드만 기억하면 되기 때문에 저장 공간의 수요가 비교적 적다
• 모든 노드를 탐색할 때 활용하기 좋다.
  - 그렇지만 완전탐색용은 아니다.(단방향이거나 끊겨있는 경우 탐색 불가)

---

BFS

Ideas

• 너비 우선 탐색 (Breadth First Search): 정점들과 같은 레벨에 있는 노드들(형제 노드)을 먼저 탐색
• 자료구조 큐 사용

How To

1. queue 역할을 하는 리스트를 만들어 시작점 (start)를 추가
2. 해당 노드를 방문처리
3. queue에서 하나씩 빼며 방문 여부를 확인, 방문하지 않은 경우 queue에 추가하고 방문처리

Code

graph = [
    [],
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]
N = len(graph)
visited = [False] * N

# BFS, queue 사용
from collections import deque


def bfs(graph, start, visited):  # 시작점 start
    queue = deque([start])  # 사용할 Queue
    visited[start] = True  # 방문처리

    while queue:
        v = queue.popleft()  # 시작점 v
        print(v, end=' ')

        for i in graph[v]:
            if visited[i] == 0:
                queue.append(i)
                visited[i] = True
bfs(graph, 1, visited)
# 1 2 3 8 7 4 5 6

Analysis

• 노드의 수: V, 간선 수: E일 때 BFS의 시간복잡도: O(V+E)
• 검색 속도는 DFS에 비해 빠르다.

---

참고문헌: https://www.fun-coding.org/daveblog.html