Merge Sort (병합 정렬)

Idea

• Divide & Conquer 사용
  - 절반씩 합치면서 정렬하면 전체 리스트 정렬
• $O(NlogN)$의 시간복잡도

참고 : https://visualgo.net/en/sorting

출처: 위키피디아

How To

1. 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
2. 각 부분 리스트를 재귀적으로 정렬한다.
3. 두 리스트를 다시 하나의 정렬된 리스트로 합병한다.

Code

array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]

def merge_sort(array):
    if len(array) <= 1:
        return array
    mid = len(array) // 2
    left = merge_sort(array[:mid])
    right = merge_sort(array[mid:])
    i, j, k = 0, 0, 0
    while i < len(left) and j < len(right):
        if left[i]< right[j]:
            array[k] = left[i]
            i += 1
        else:
            array[k] = right[j]
            j += 1
        k += 1

    if i ==  len(left):
        while j < len(right):
            array[k] = right[j]
            j += 1
            k += 1
    elif j == len(right):
        while i < len(left):
            array[k] = left[i]
            i += 1
            k += 1
    return array

merge_sort(array)
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Analysis

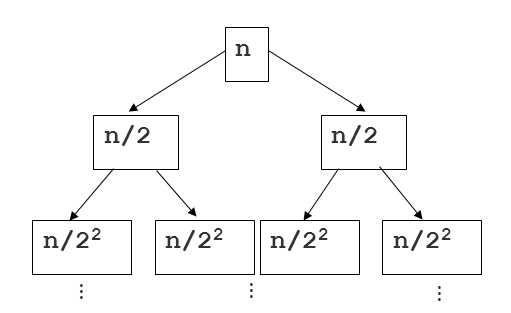
• 나누는 각 단계의 시간 복잡도 = O(N)
  - 깊이 i에 따른 노드의 수 = 2^i
  - 깊이 i에 따른 리스트의 길이 = n/2^i

• 각 깊이에서는 log2N만큼 만들어짐

• 따라서 각 단계별 시간복잡도 = O(NlogN)

  

---

Quick Sort (퀵 정렬)

Idea

• 대표적인 정렬 알고리즘
• 기준 데이터(Pivot)를 설정하고, 큰 수와 작은 수를 교환한 후 리스트를 반으로 나눈다
  - 피벗: 큰 수와 작은 수를 교환할 때 사용되는 '기준'
  - 리스트에서 첫 번째 데이터를 피벗으로 정하는 호어 분할(Hore Partition)방식 활용

How To

1. 리스트에서 첫 번째 데이터를 피벗으로 정의
2. 왼쪽부터 피벗보다 큰 데이터 찾기
3. 오른쪽부터 피벗보다 작은 데이터 찾기
4. 데이터 위치 교환
5. 위의 과정을 반복
6. 리스트 개수가 1개이면 return

Code

방법 1. Hore Partition 사용

array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]

def quick_sort(array, start, end):
    # 종료조건
    if start >= end:  # 원소가 1개인 경우 return
        return
    
    pivot = start  # 피벗은 첫 번째 원소
    left = start+1
    right = end
    while left < right:
        # 피벗보다 큰 데이터 찾기
        while left <= end and array[left] <= array[pivot]:
            left += 1
        # 피벗보다 작은 데이터 찾기
        while right > start and array[right] >= array[pivot]:
            right -= 1
        # 엇갈리면 작은 데이터와 피벗 교체
        if left > right:
            array[right], array[pivot] = array[pivot], array[right]
        # 엇갈리지 않으면 작은 데이터와 큰 데이터 교체
        else:
            array[left], array[right] = array[right], array[left]
            
    # 분할 이후 왼쪽과 오른쪽에서 정렬 수행(재귀)
    quick_sort(array, start, right-1)
    quick_sort(array, right+1, end)
    
quick_sort(array, 0, len(array)-1)

print(array)
# [0, 1, 2, 4, 3, 5, 6, 8, 7, 9]    

방법 2.

array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]

def quick_sort(array):
    # 종료조건
    if len(data) <= 1:  # 하나 이하의 원소를 가지고있으면 종료
        return array
    
    left = []  # 분할된 왼쪽 부분
    right = []  # 분할된 오른쪽 부분
    pivot = array[0]  # 피벗은 첫 번째 원소
    
    for index in range(1, len(array)):
        if pivot > array[index]:
            left.append(array[index])
        else:
            right.append(array[index])
            
    # 분할 이후 왼쪽과 오른쪽 부분에서 정렬(재귀) 후 전체 리스트 반환
    return quick_sort(left) + [pivot] + quick_sort(right)

print(quick_sort(array))
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Analysis

• 시간 복잡도 = $O(NlogN)$
• 이미 데이터가 정렬되어있는 경우 매우 느리게 동작
• 최악의 경우 시간 복잡도 = $O(N^2)$
  - 맨 처음 pivot이 가장 크거나 가장 작을 때