AVL TREE

AVL는 왜 필요할까?

AVL TREE는 기본적으로 BST의 단점을 보안하기 위해 고안되었다. BST의 단점은 차례대로 순서가 계속 증가하는 값이나 아니면 반대로 차례대로 계속 순서가 감소하는 값이 들어올때 BST의 삽입 규칙에 따라 한쪽으로 편향된 Tree가 만들어진다는 점이다. 따라서 평균적인 BST의 탐색/삽입/삭제의 시간복잡도는 O(logN)이지만, 최악의 시간복잡도는 O(N)이 된다.

이 문제를 보안하기 위해 AVL Tree가 등장하게 되었는데, 간단하게 설명하면 왼쪽과 오른쪽의 subtree의 높이를 서로 맞춰주면서 Tree를 만들어나가는 자료구조이다.

AVL 키워드

Balance Factor, 4가지 회전(LL회전, LR회전, RL회전, RR회전)

BF 구하는 법

BF는 왼쪽 subtree와 오른쪽 subtree의 높이 차이를 구해 자가 균형을 맞추기 위해 만들어진 상수이다. BF값이 양수이면 부모 노드를 포함한 왼쪽 subtree를 일차적으로 조정하고, BF값이 음수이면 부모를 포함한 오른쪽 subtree를 조정한다.

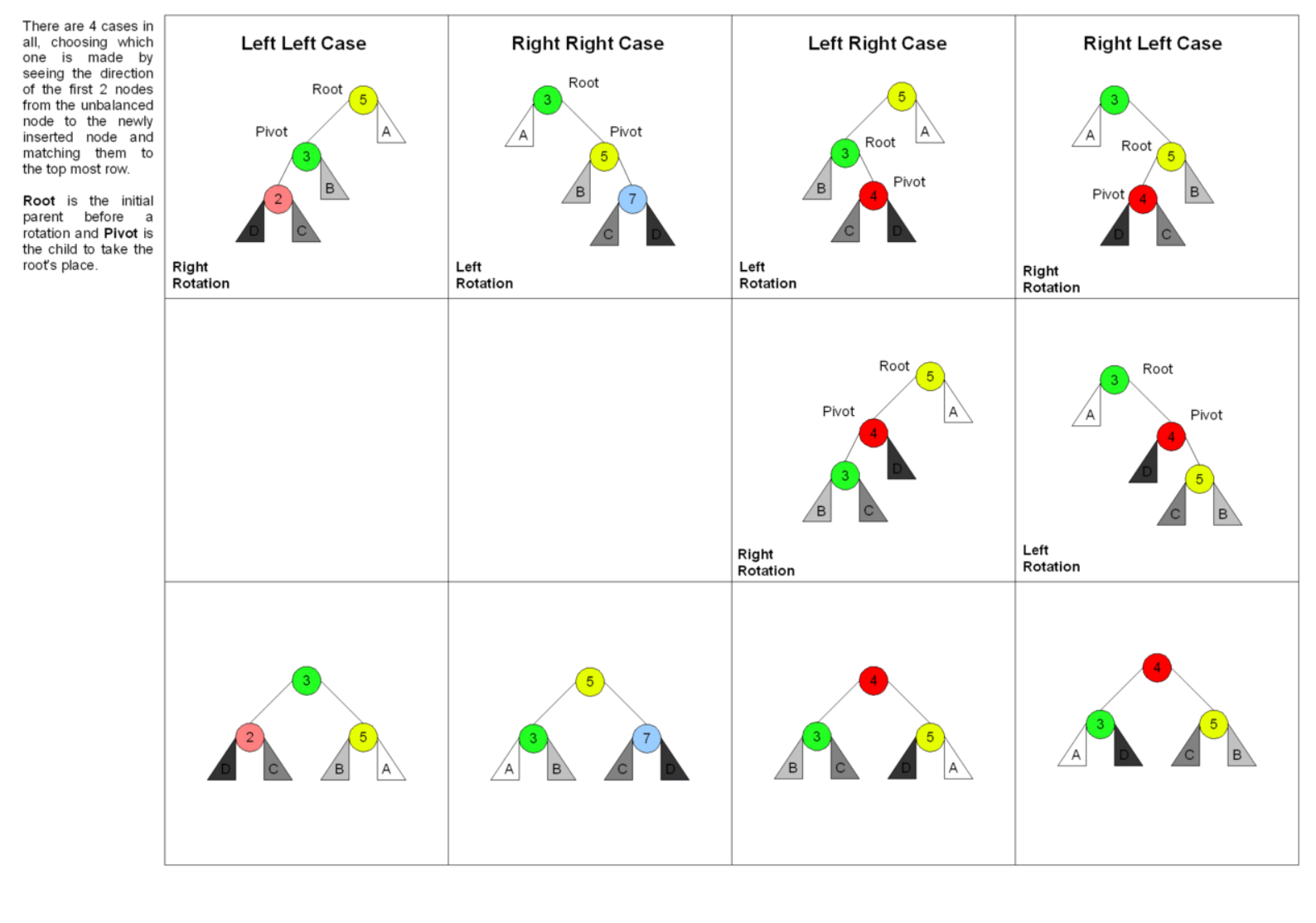
AVL Tree에서 트리를 조정하는 방법에는 총 4가지의 경우가 있을 수 있는데, LL회전, LR회전, RL회전, RR회전이 그것이다. LL과 RR 같은 경우에는 가운데 노드를 부모로 승격시키고, LR과 RL같은 경우에는 마지막 노드를 부모로 승격시킨다.

AVL에서의 Insert/Delete

AVL에서의 Insert와 Delete는 이해하기 쉽다. 먼저 BST의 규칙에 의거해서 삽입과 삭제를 실행하고 그다음, AVL balance factor를 보면서 트리를 재조정한다.