B-tree
인덱스를 이루고 있는 자료구조의 일종이다.
B-tree에서 'B'는 정확히 어떤 의미라고 밝혀진 바는 없다. 아마 'Balanced'를 의미하는 'B'가 아닐까라는 추측만 있다. MySQL의 DB engine인 InnoDB는 B+tree로 이뤄져있는데, B-tree의 확장된 개념이다. B-Tree는 데이터베이스의 인덱싱 알고리즘 가운데 가장 일반적으로 사용되고, 또한 가장 먼저 도입된 알고리즘입니다. 하지만 아직도 가장 범용적인 목적으로 사용되는 인덱스 알고리즘이다. B-Tree에는 여러 가지 변형된 형태의 알고리즘이 있는데, 일반적으로 DBMS에서는 주로 B+-Tree 또는 B*-Tree가 사용된다. 인터넷상에서 쉽게 구할 수 있는 B-Tree의 구조를 설명한 그림 때문인지 많은 사람들이 B-Tree의 "B"가 바이너리(이진) 트리라고 잘못 생각하고 있다. 하지만 B-Tree의 "B"는 "Binary(이진)"의 약자가 아니라 "Balanced"를 의미한다.
B-Tree는 컬럼의 원래 값을 변형시키지 않고 (물론 값의 앞부분만 잘라서 관리하기는 하지만) 인덱스 구조체 내에서는 항상 정렬된 상태로 유지하고 있습니다. 전문 검색과 같은 특수한 요건이 아닌 경우, 대부분 인덱스는 거의 B-Tree를 사용할 정도로 일반적인 용도에 적합한 알고리즘입니다.
구조 및 특성
B-Tree 인덱스를 제대로 사용하려면 B-Tree의 기본적인 구조는 알고 있어야 한다. B-Tree는 트리 구조의 최상위에 하나의 "루트 노드"가 존재하고 그 하위에 자식 노드가 붙어 있는 형태이다. 트리 구조의 가장 하위에 있는 노드를 "리프 노드"라 하고, 트리 구조에서 루트 노드도 아니고 리프 노드도 아닌 중간 노드를 "브랜치 노드"라고 한다. 데이터베이스에서 인덱스와 실제 데이터가 저장된 데이터는 따로 관리되는데, 인덱스의 리프 노드는 항상 실제 데이터 레코드를 찾아가기 위한 주소 값을 가지고 있다.
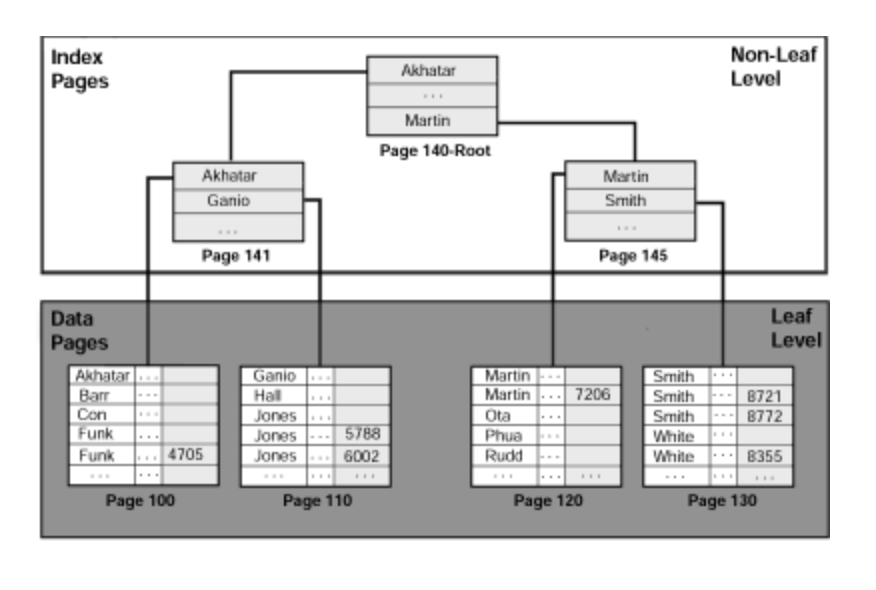
인덱스의 키값은 모두 정렬돼 있지만 데이터 파일의 레코드는 정렬돼 있지 않고 임의의 순서대로 저장돼 있다. 많은 사람이 데이터 파일의 레코드는 INSERT된 순서대로 저장되는 것으로 생각하지만 그렇지 않다. 만약 테이블의 레코드를 전혀 삭제나 변경없이 INSERT만 수행한다면 맞을 수도 있다. 하지만 레코드가 삭제되어 빈 공간이 생기면 그다음의 INSERT는 가능한 삭제된 공간을 재활용하도록 DBMS가 설계되기 때문에 항상 INSERT된 순서로 저장되는 것은 아니다.
대부분 RDBMS의 데이터 파일에서 레코드는 특정 기준으로 정렬되지 않고 임의의 순서대로 저장된다. 하지만 InnoDB 테이블에서 레코드는 클러스터되어 디스크에 저장되므로 기본적으로 프라이머리 키 순서대로 정렬되어 저장된다. 이는 오라클 IOT(Index organized table)나 MS-SQL의 클러스터 테이블과 같은 구조를 말한다. 다른 DBMS에서는 클러스터링 기능이 선택 사항이지만, InnoDB에서는 사용자가 별도의 명령이나 옵션을 선택하지 않아도 디폴트로 클러스터링 테이블이 생성된다. 클러스터링이란 비슷한 값들은 최대한 모아서 저장하는 방식을 의미한다.
인덱스는 테이블의 키 컬럼만 가지고 있으므로 나머지 컬럼을 읽으려면 데이터 파일에서 해당 레코드를 찾아야 한다. 이를 위해 인덱스의 리프 노드는 데이터 파일에 저장된 레코드의 주소를 가지게 된다. "레코드 주소"는 DBMS 종류나 MySQL의 스토리지 엔진에 따라 의미가 달라진다. 오라클은 물리적인 레코드 주소가 되지만 MyISAM 테이블에서는 내부적인 레코드의 아이디(번호)를 의미한다. 그리고 InnoDB 테이블에서는 프라이머리 키에 의해 클러스터링되기 때문에 프라이머리 키값 자체가 주소 역할을 한다. 실제 MySQL 테이블의 인덱스는 항상 인덱스 컬럼 값과 주소 값(MyISAM의 레코드 아이디 값 또는 InnoDB의 프라이머리 키값)의 조합이 인덱스 레코드로 구성된다.
트리 구조의 우위성
트리 구조는 꼭 데이터베이스에 한정하지 않더라도 시스템 세계에서는 데이터를 유지하기 위해 자주 사용하는 구조이다. '탐색' 시 단시간 내에 실행할 수 있기 때문이다. B-tree의 핵심은 데이터가 정렬된 상태로 유지되어 있다는 것이다.
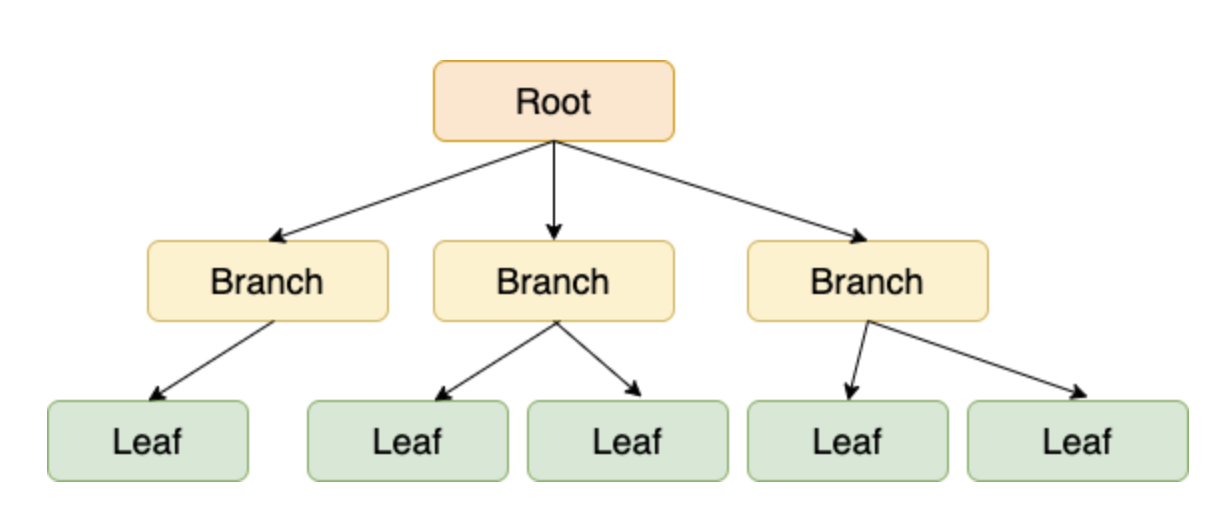
그림에 표시된 사각형으로 표시된 한 개 한 개의 데이터를 '노드(Node)'라고 한다.
가장 상단의 노드를 '루트 노드(Root Node)', 중간 노드들을 '브랜치 노드(Branch Node)', 가장 아래 노드들을 '리프 노드(Leaf Node)'라고 한다.
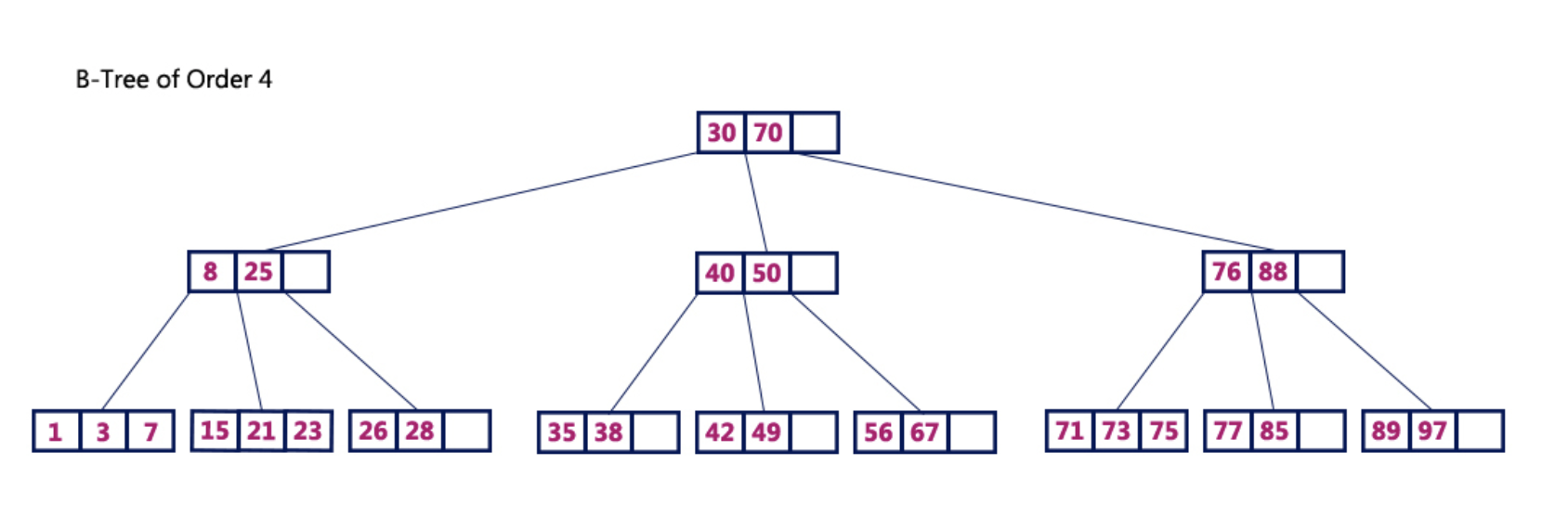
B-tree는 Binary search tree와 유사하지만, 한 노드 당 자식 노드가 2개 이상 가능하다. key 값을 이용해 찾고자 하는 데이터를 트리 구조를 이용해 찾는 것이다.
왜 B-tree는 빠른가
B-tree의 장점 한 가지는 '어떤 값에 대해서도 같은 시간에 결과를 얻을 수 있다'인데, 이를 '균일성'이라고 한다.
위의 예시에서 리프노드에 있는 '15'나 '28'을 찾는 시간은 동일할 것이다.(트리 높이가 다른 경우, 약간의 차이는 있겠지만 O(logN)이라는 시간 복잡도를 구할 수 있다.)
만약 선형탐색일 경우 어떨까?
리프노드에 있는 값들만 따져보면,
[1, 3, 7, 15, 21 .... 85, 89, 97]
'15', '28'을 찾기 위해서는 배열을 하나씩 체크하는 수 밖에 없고 시간은 더욱 소요된다. (시간복잡도 : O(n))
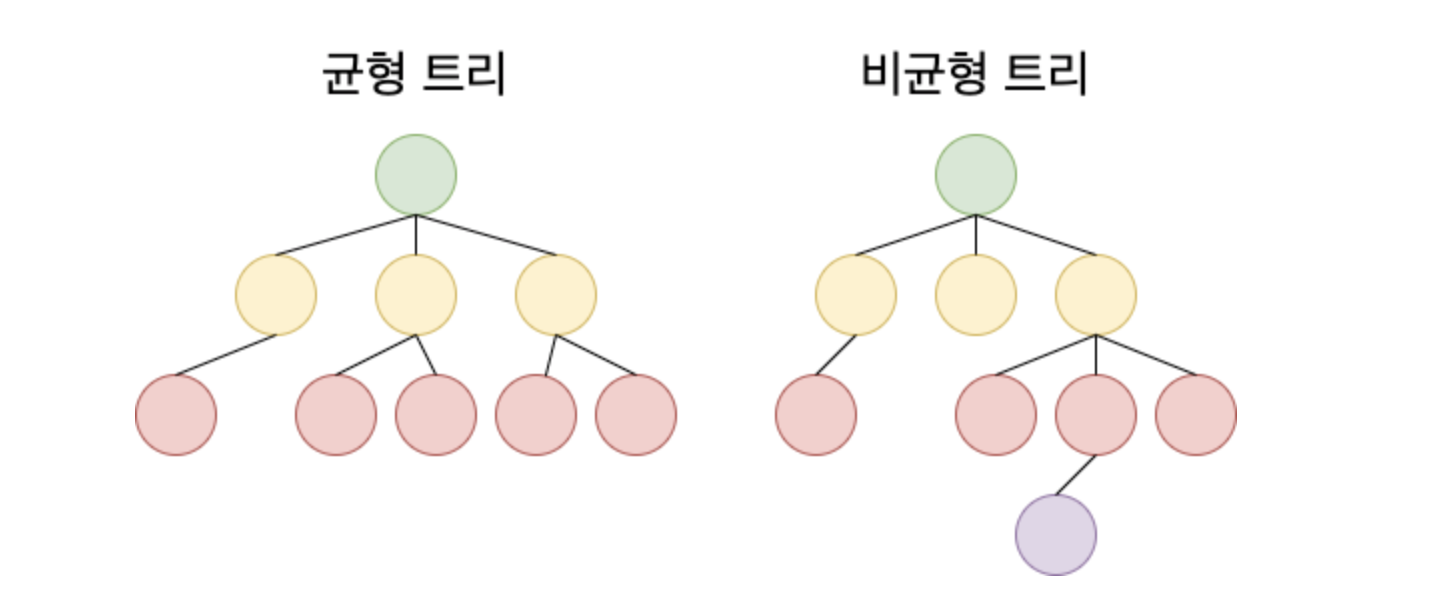
'균형 트리'란 루트로부터 리프까지의 거리가 일정한 트리 구조를 뜻하는 것으로, 트리 중에서 특히 성능이 안정화 되어있다.
그러나, B-tree 처음 생성 당시는 균형 트리이지만 테이블 갱신(INSERT/UPDATE/DELETE)의 반복을 통해 서서히 균형이 깨지고, 성능도 악화된다.
어느 정도 자동으로 균형을 회복하는 기능이 있지만, 갱신 빈도가 높은 테이블에 작성되는 인덱스 같은 경우 인덱스 재구성을 해서 트리의 균형을 되찾는 작업이 필요하다.
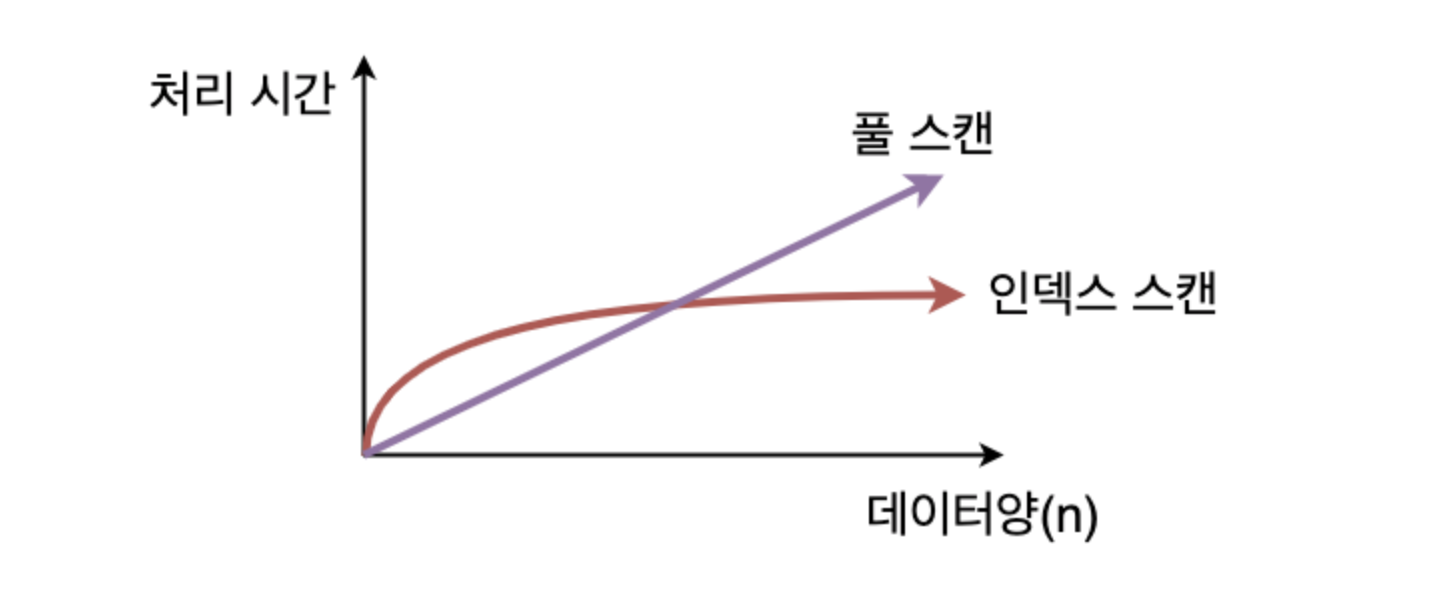
풀 스캔이 테이블의 크기에 비례하는 형태로 실행 시간이 늘어가는데에 비해 인덱스를 사용한 경우 실행 시간의 저하는 보통 원만한 곡선을 그리게 된다.
B+tree
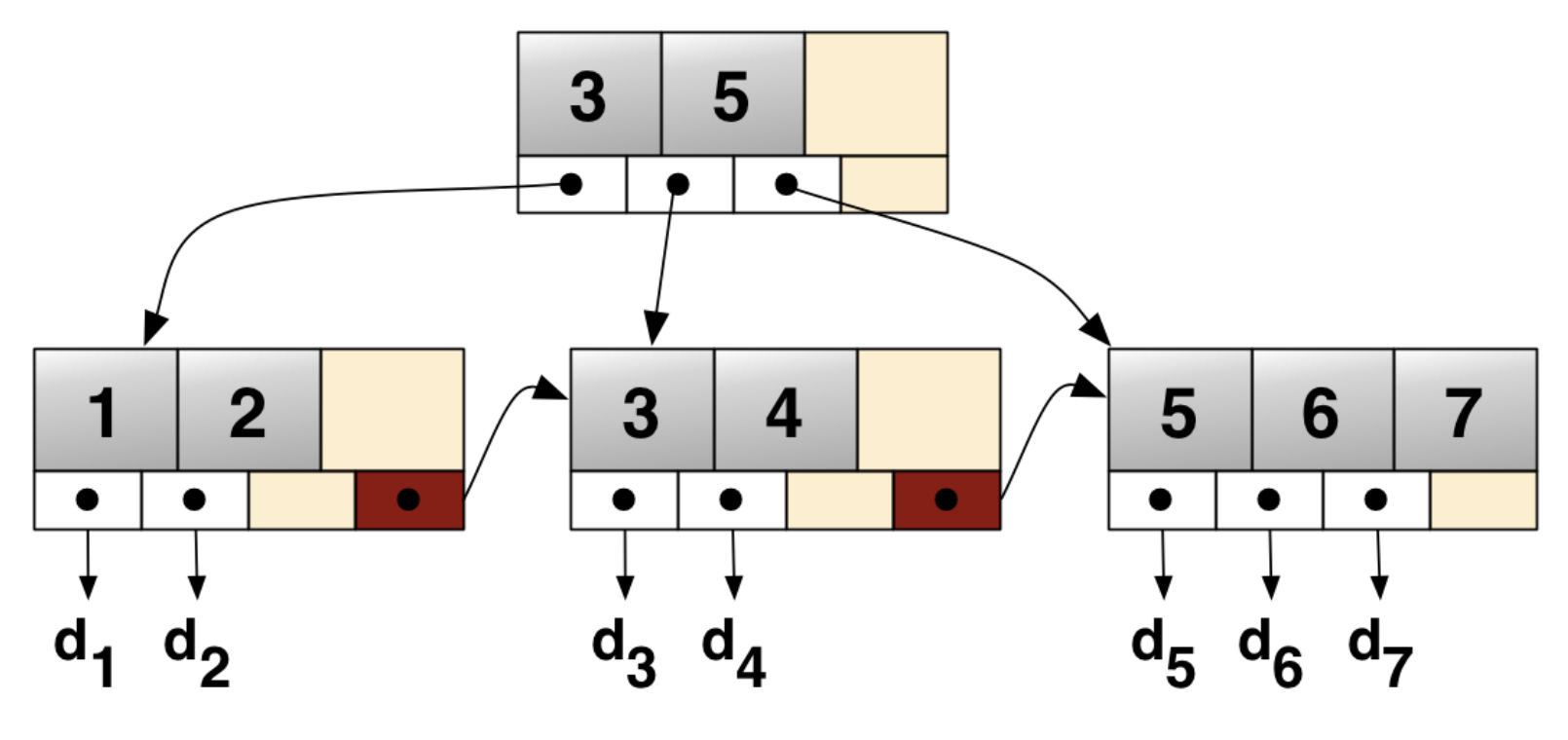
B+tree는 B-tree의 확장개념으로, B-tree의 경우, internal 또는 branch 노드에 key와 data를 담을 수 있다. 하지만, B+tree의 경우 브랜치 노드에 key만 담아두고, data는 담지 않는다. 오직 리프 노드에만 key와 data를 저장하고, 리프 노드끼리 Linked list로 연결되어 있다.
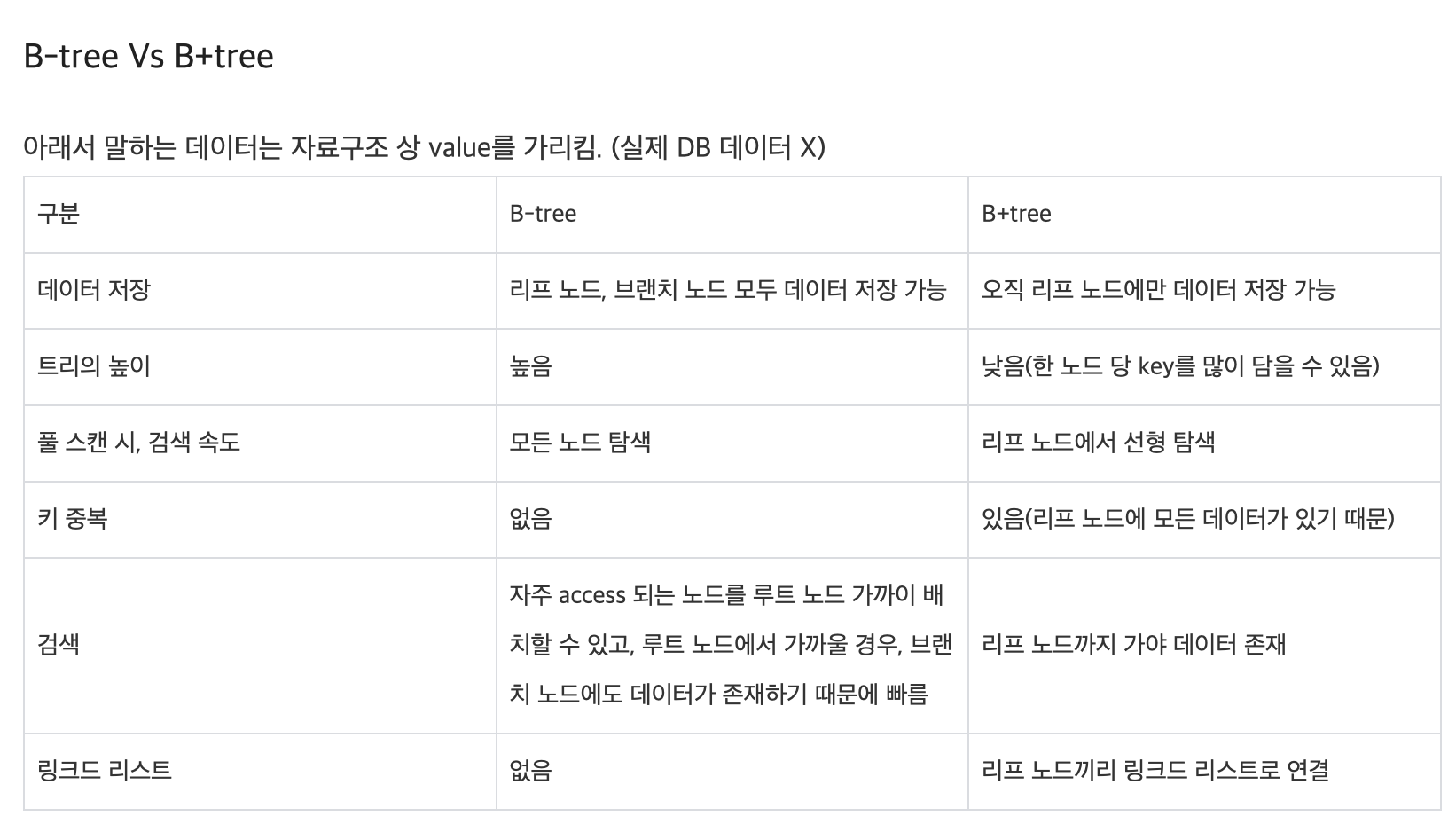
B+tree 장점
- 리프 노드를 제외하고 데이터를 담아두지 않기 때문에 메모리를 더 확보함으로써 더 많은 key들을 수용할 수 있다. 하나의 노드에 더 많은 key들을 담을 수 있기에 트리의 높이는 더 낮아진다.(cache hit를 높일 수 있음)
- 풀 스캔 시 B+tree는 리프 노드에 데이터가 모두 있기 때문에 한 번의 선형탐색만 하면 되기 때문에 B-tree에 비해 빠르다. B-tree의 경우에는 모든 노드를 확인해야 한다.
참고: https://12bme.tistory.com/138
https://zorba91.tistory.com/293
