정렬 알고리즘?
- 목록 안에 저장된 요소들을 특정한 순서대로 재배치하는 알고리즘
- 좀 더 효율적인 알고리즘을 사용하기 위해 사용
정렬시 고려사항
- 정렬할 데이터의 양
- 데이터와 메모리
- 이미 정렬된 저도
- 필요한 추가 메모리의 양
- 상대위치 보존여부(안전성) 등
정렬 알고리즘 7가지
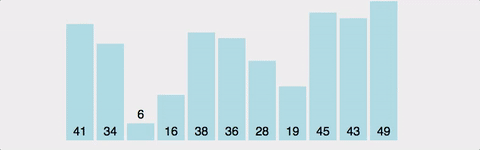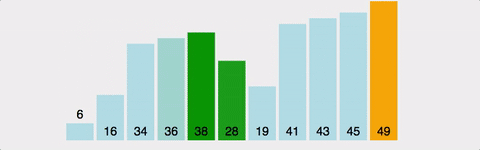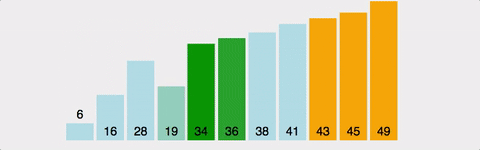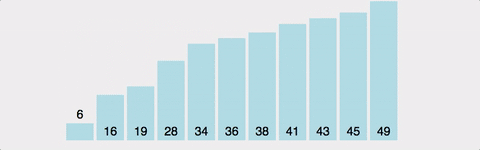
- 버블 정렬 (Bubble Sort)
: 인접한 두 수를 비교하여 오름차순 또는 내림차순으로 정렬하는 알고리즘 / O(N^2)
- 장점
- 안정성 보장
- 구현이 매우 간단하고, 직관적이다.
- 단점
- 데이터를 하나씩 비교하기 때문에 비교 횟수가 많아지므로 시간이 오래 걸린다.
- 정렬된 상태에서 새로운 데이터가 추가되면 정렬 효율이 좋지 않다.
- 선택 정렬(Selection Sort)
: 주어진 배열에서 최소값을 반복적으로 찾아 정렬하는 알고리즘
/ O(N^2)
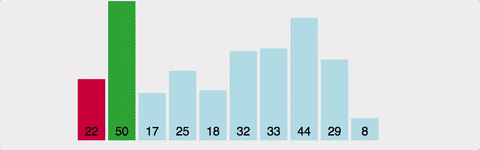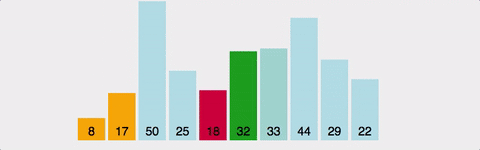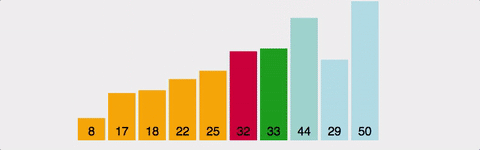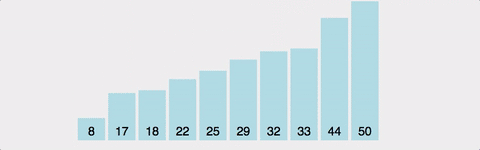
-
장점
- 버블 정렬과 마찬가지로 구현이 간단하다.
- 비교하는 횟수에 비해 교환하는 횟수가 적어, 많은 교환이 일어나야 하는 자료 상태에서 비교적 효율적이다.
-
단점
- 데이터를 하나씩 비교하기 때문에 비효율적이다.
- 정렬된 상태에서 새로운 데이터가 추가되면 효율이 좋지 않다.
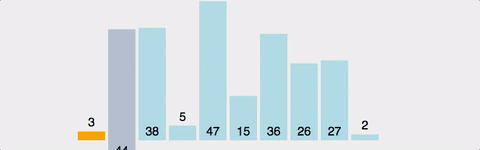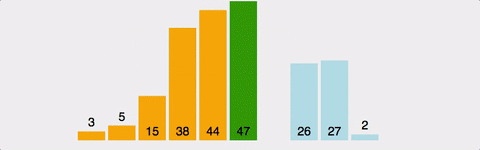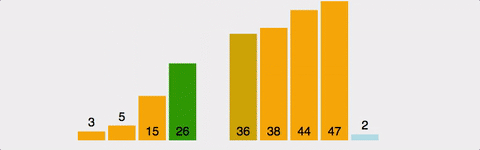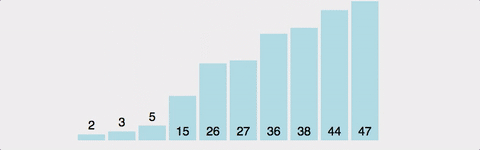
- 삽입 정렬(Insertion Sort)
: 데이터 집합을 순회하면서 정렬이 필요한 요소를 뽑아내어 다시 적당한 곳으로 삽입하는 알고리즘
-> 버블 정렬의 비효율성을 개선하기 위해 등장한 알고리즘 / O(N^2)
- 장점
- 입력으로 들어오는 배열의 값이 정렬되어 있을수록 속도가 빠르다.
- 정렬된 값은 교환이 일어나지 않는다.
- 배열에 자료를 하나씩 삽입/제거하는 경우, 최고의 정렬 알고리즘이 된다.
- 단점
- 배열의 길이가 길어질수록 비효율적이다.
- 시간복잡도가 O(N^2)으로 비효율적이다.
- 퀵 정렬(Quick Sort)
: 분할 정복 방법을 통한 정렬 알고리즘 /
최선과 평균의 경우 - O(N log N) , 최악의 경우 - O(N^2)
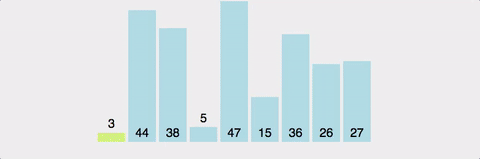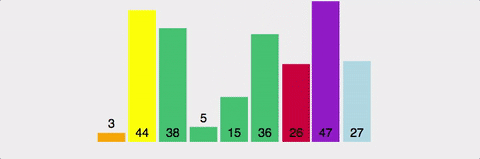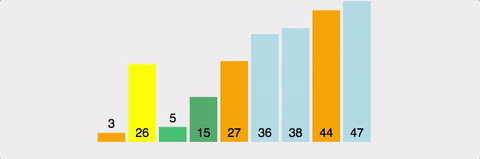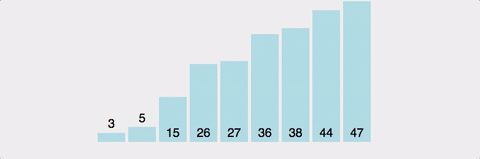
- 데이터 집합 내에 임의의 기준(pivot) 값을 정하고 해당 기준 값 집합을 기준으로 두 개의 부분 집합으로 나눈다.
- 한쪽 부분에는 기준 값보다 작은 값들을 놓고, 다른 쪽은 큰 값들만 넣는다. -> 안정성 보장 x
- 더 이상 쪼갤 부분이 없을 때까지 피벗/쪼개기를 재귀적으로 적용
- 장점
- 한번 결정된 피벗들이 추후 연산에 제외되므로, O(N log N)을 가지는 정렬 알고리즘과 비교했을때 가장 빠르다.
- 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환
- 단점
- 정렬된 배열에 대해서는 불균형 분할에 의해 수행시간이 더 많이 걸린다.
- 병할 정렬(Merge Sort)
: 배열을 작은 단위로 쪼개어 정렬한 결과를 합치면서 전체를 정렬하는 분할 정복 방식의 알고리즘 / O(N log N)
-> 빠른 정렬로 구분, 퀵 정렬과 함께 많이 언급되는 정렬 알고리즘
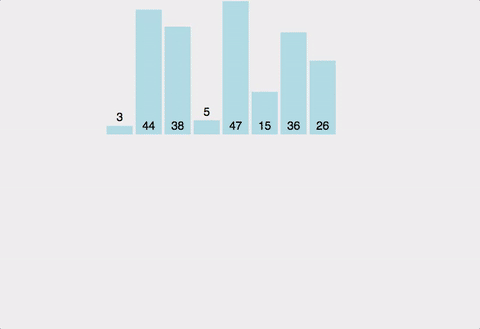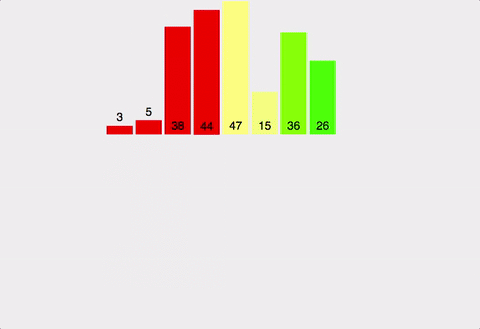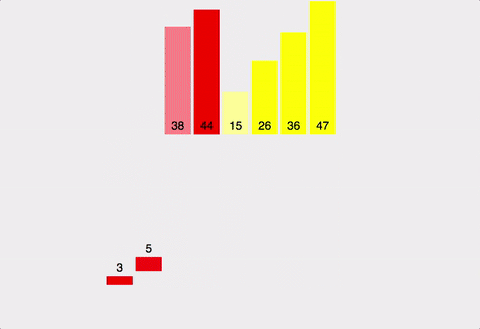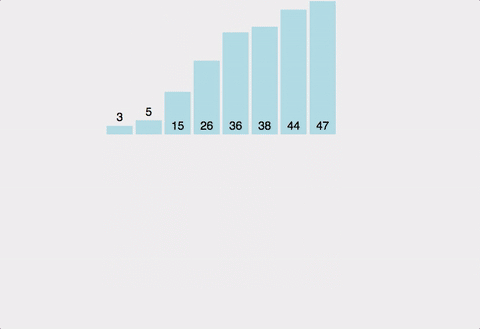
- 배열을 왼쪽 절반, 오른쪽 절반으로 분할하며 최소 단위로 쪼갠 후 정렬 진행
- 쪼갠 영역들을 차례대로 두 개씩 병합
-
장점
- 항상 일정한 시간 복잡도 O(N log N)를 가진다.
-
단점
- 정렬을 하는 배열 외의 추가적인 임시 배열(메모리)이 필요하다.
- 힙 정렬(Heap Sort)
: 최대 힙 트리나 최소 힙 트리를 구성하여 정렬하는 알고리즘
-> 안정성 보장 x / O(N log N)

- 장점
- 가장 크거나 가장 작은 값을 구할 때 유용 -> 한 번의 힙 구성을 통해 구하는 것이 가능
- 멀리 떨어진 요소들을 정렬할 때 유용
- 항상 같은 시간 복잡도를 가지므로 성능이 준수하다.
- 단점
- 같은 시간 복잡도를 다른 정렬 알고리즘과 비교하면 느린 편이다.
- 기수 정렬(Radix Sort)
: 가장 낮은 자리수부터 비교해가면 정렬하는 알고리즘
/ O(dN) -> d는 최대 자리수

- 장점
- 비교없는 O(N)의 시간복잡도를 가진다.
- 문자열, 정수 정렬 가능
- 단점
- 자릿수가 없는 것은 정렬할 수 없다.
- 추가적인 메모리 공간이 필요