백트래킹이란?

처음 알고리즘을 모르고 백준 문제를 풀 때, 재귀와 백트래킹이 무엇이 다른지 그리고 DFS가 뭔지 알지 못해서 너무나 어려웠다.
특히 N과 M 문제를 끼워 맞추듯 풀었던 기억이 있는데..
이번 기회에 정리해보고자 한다.
15649 N, M(1)

문제는 간단하다. N개의 자연수에서 M개를 고른 수열을 모두 출력하라는 것이다.
개수를 구하는 것은 간단하다. N Permutation M을 구하면 되니까.
경우의 수를 모두 구하는 것도 직접 종이에 쓰면서 하면 전혀 어려운 일이 아니지만, 이를 코드로 구현하는 것은 그렇게 쉽지 않다. 특히 처음하는 경우에는 더더욱 그렇다.

예시로 6개의 자연수에서 2개를 뽑아 중복 없는 수열을 만들어보자.

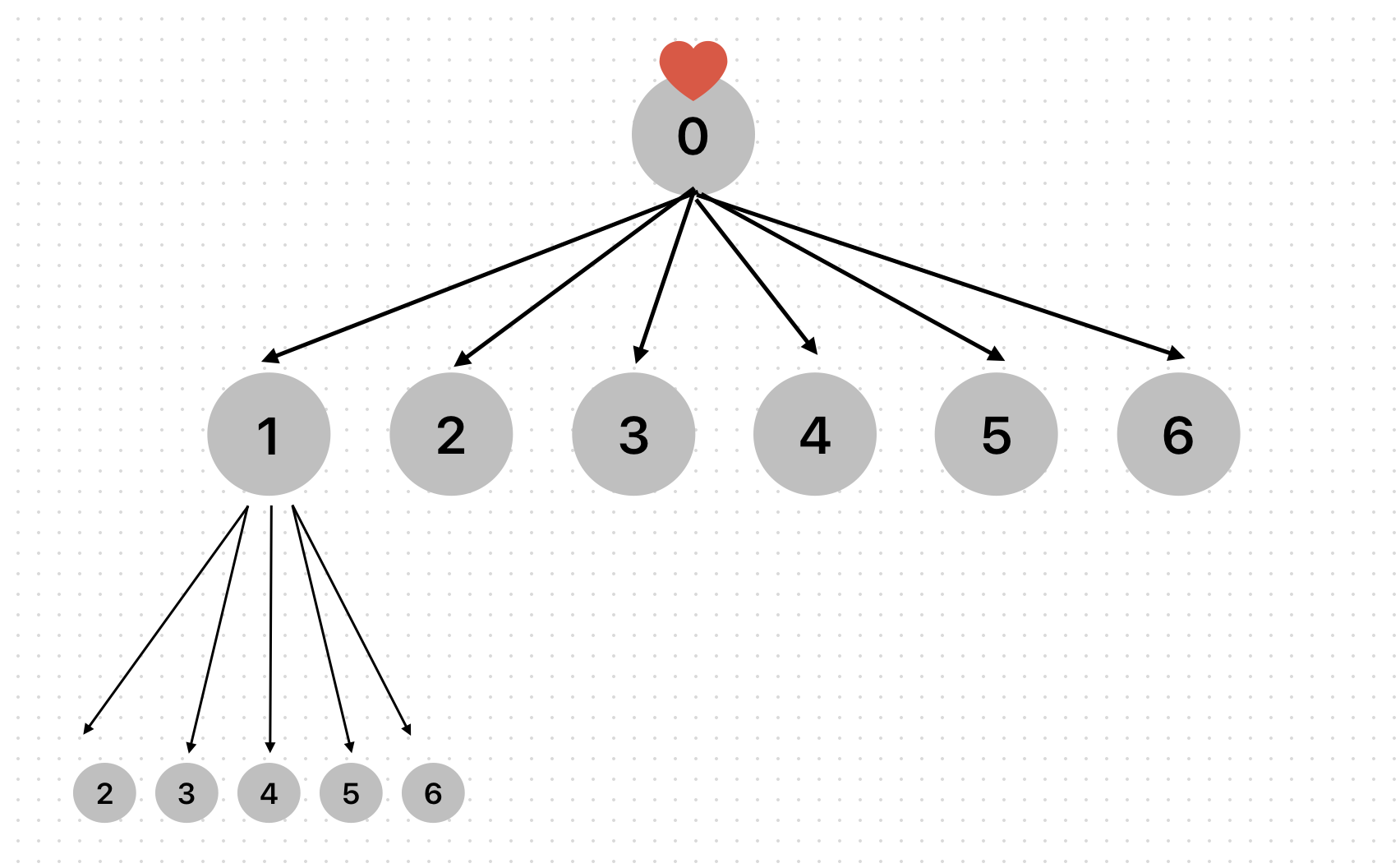
누구나 위와 같은 그림을 그릴 수 있다. 그리고 누구나 이렇게 하나하나 셀 것이다.
당연하게도 위와 같은 사고과정을 코드로 옮겨 주면 된다.

코드로 구현하기 전에 알고리즘을 먼저 말로써 표현해보자. 어떤 순서로 짜면 될까?

1. 첫 번째 자연수 부터 시작한다.
   출력해야 하므로 어딘가에 저장해놓는다.
2. 다음 자연수로 이동한다.
   중복을 허용하지 않으므로 자연수를 increment한다.
   마찬가지로 어딘가에 저장해놓는다.
3. 2개를 모두 골랐으므로, 이전 상태로 돌아간다.
4. 다시 자연수를 increment한다
   ...

여기서 3번이 백트래킹의 핵심이다. 탈출 조건에 도착했을 때 작업을 수행하고 이전 단계로 돌아가는 것. 이전 단계를 당연히 기억하고 있어야 한다.
그렇기 때문에 방문 정보를 담을 변수가 따로 필요하다. bool visited[]를 이용하자.
그리고 탐색하는 과정이 DFS의 과정을 따른다. DFS를 모르더라도 괜찮다. 일단 위 알고리즘을 하나씩 코드로 구현하여 보자.

1~N까지 자연수를 M-th depth까지 탐색하는 함수를 선언하면 된다.
가장 먼저 argument를 어떻게 받을지 정해야 한다.
몇 번째 깊이인지 알려주는 cnt 변수와 지금 가리키는 자연수의 위치를 알려주는 idx변수를 argument로 받으면 된다.
void dfs(int idx, int cnt)
이렇게 선언하자.

void dfs(int idx, int cnt){
	if(cnt == m){
    // Print visited numbers
	}

그리고 함수의 Body를 작성해야 한다.
1. 어딘가의 현재 idx의 자연수를 저장하고
2. 자연수를 increment 시켜서 다음 depth로 넘어간다.(재귀)
3. 제일 깊은 곳을 찍고 돌아왔을 때 다음 자연수로 넘겨줘야 한다.

그림을 통해 이해해보자.

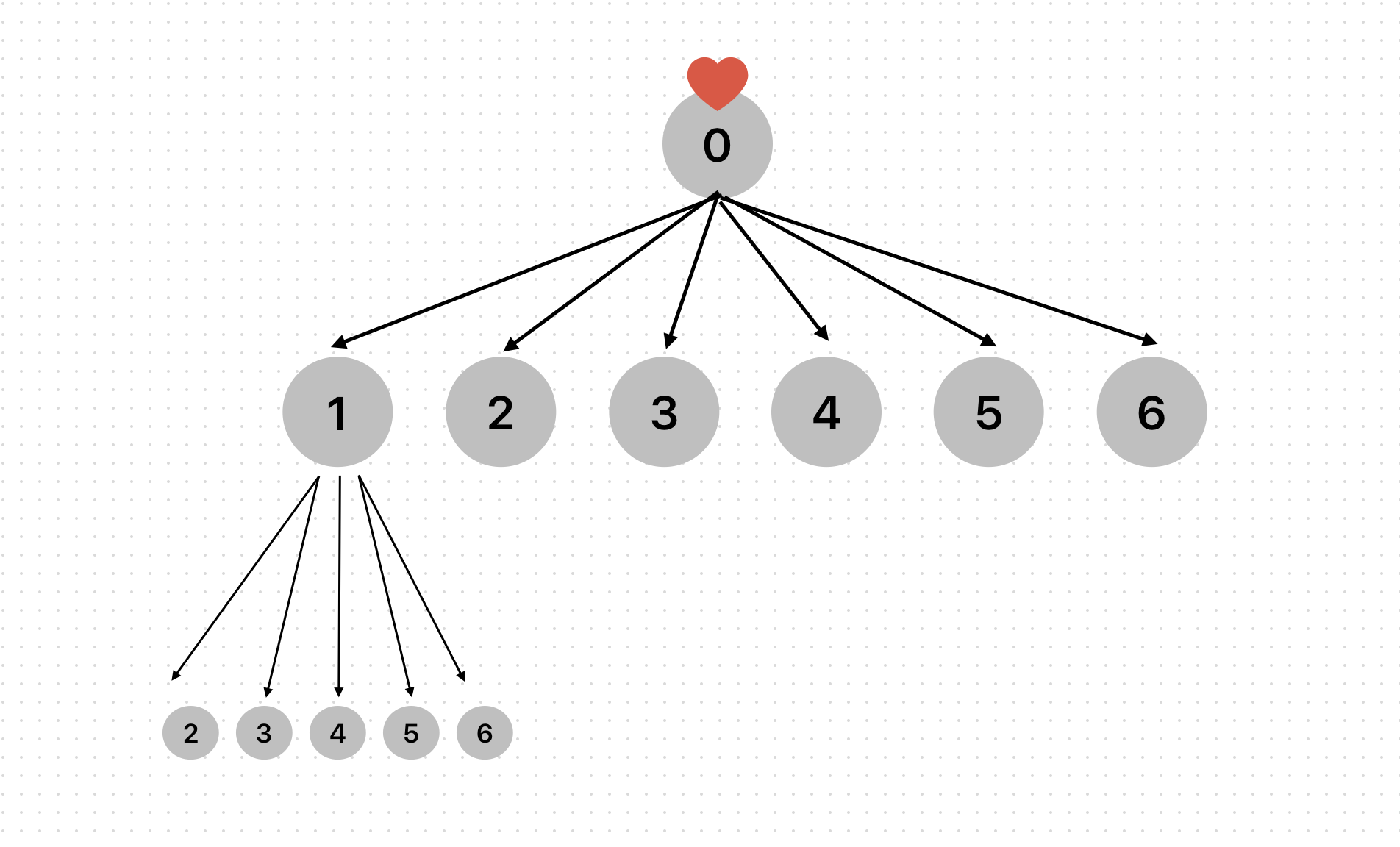
main 함수에서 dfs(0, 0)를 호출하면 하트의 위치에서 탐색을 시작할 것이다.
그렇다면 이제 6개의 화살표를 쏴줘야 한다. 1~6을 모두 탐색해야 한다.
자연스럽게 for문으로 한 바퀴 돌려보자는 생각이 든다.

for(int i = 1; i <= n; i++){
	dfs(i, cnt + 1); // depth++, i = current num.
    }

해야할 일이 세가지 더 남았다.
자연수를 저장하고, 방문 표시를 남기고, 돌아왔을 때 다음 자연수로 넘겨줘야 한다.
저장은 전역변수 int ans[]를 이용하면 될 것이고, 방문 표시는 visited = true로 설정한다.
돌아왔을 때 다음 자연수로 넘겨주는 것이 핵심이다.

이를 이해하는 것이 제일 중요하기 때문에 그림을 통해 과정을 이해해보자.

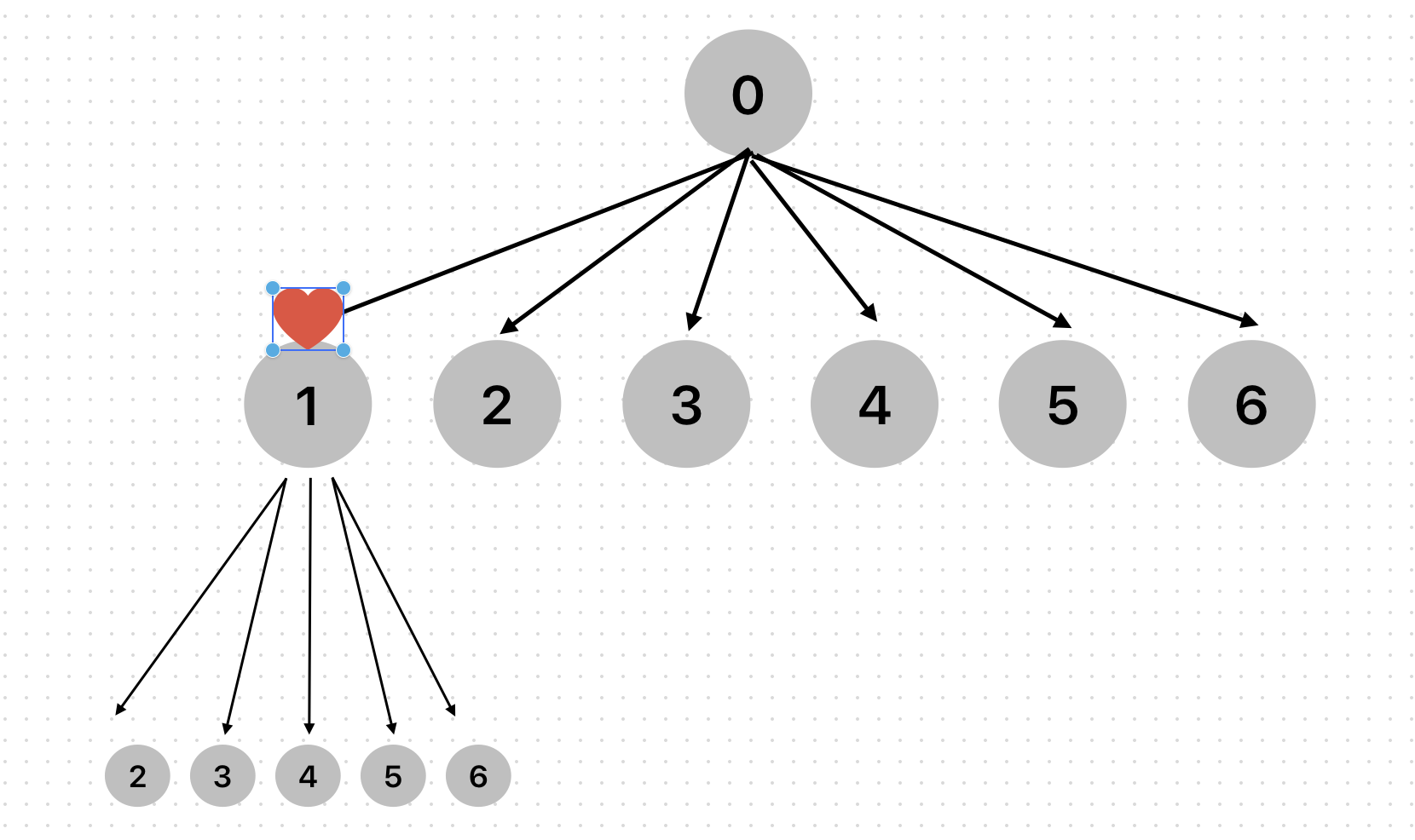
먼저 깊이 1에서 1을 탐색한다. ans배열에 1이 저장되었다.
한 칸 더 내려가자.

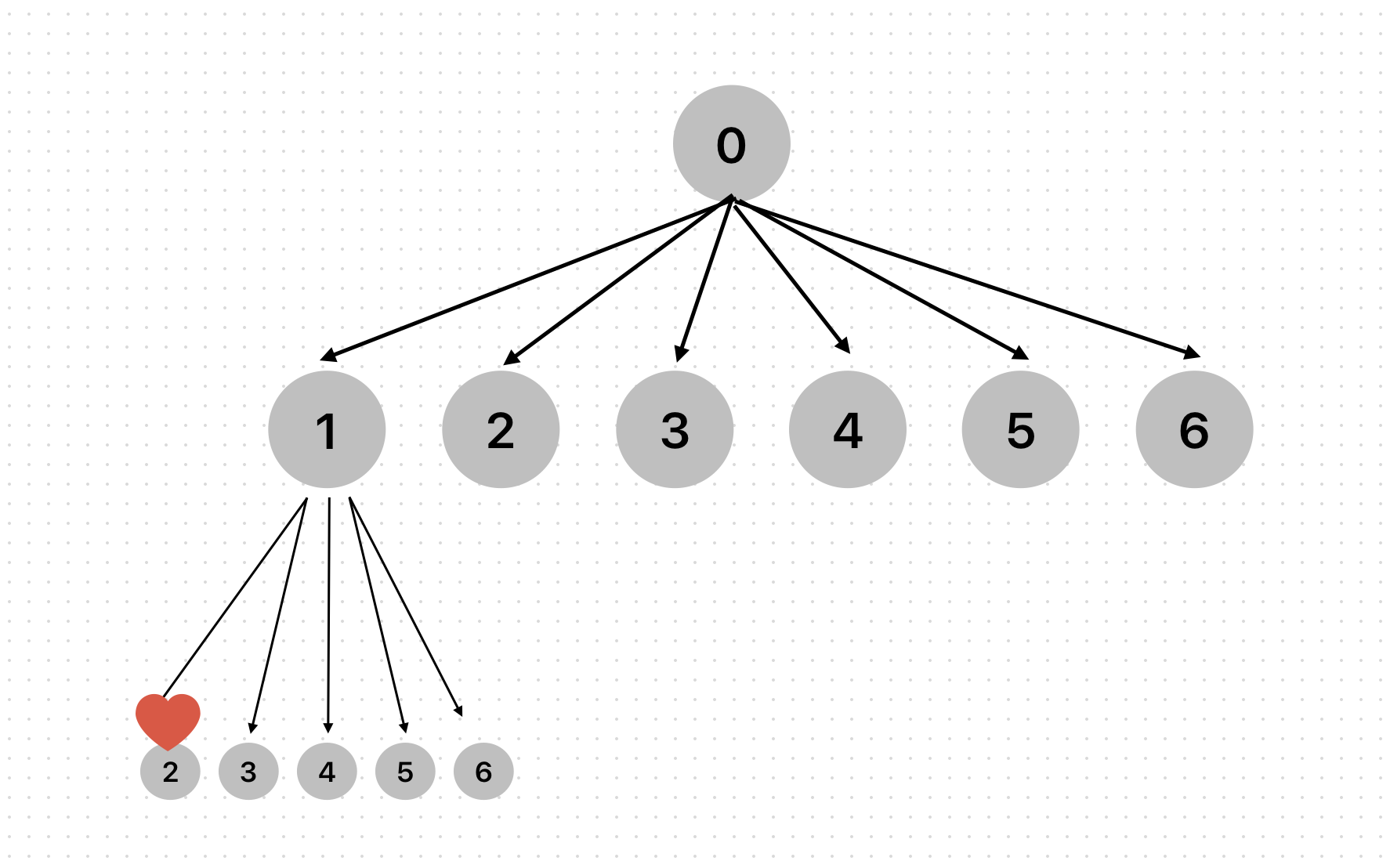
깊이 2에서 2를 탐색하고 2를 저장한다. 이때 cnt 값은 1이다.
한 칸 더 내려가면 탈출 조건에 걸려서 저장된 1, 2를 출력한다.
return; 되는 순간 어디로 돌아가는가??
깊이 1의 1을 가리키는 곳으로 돌아갈 것이다.

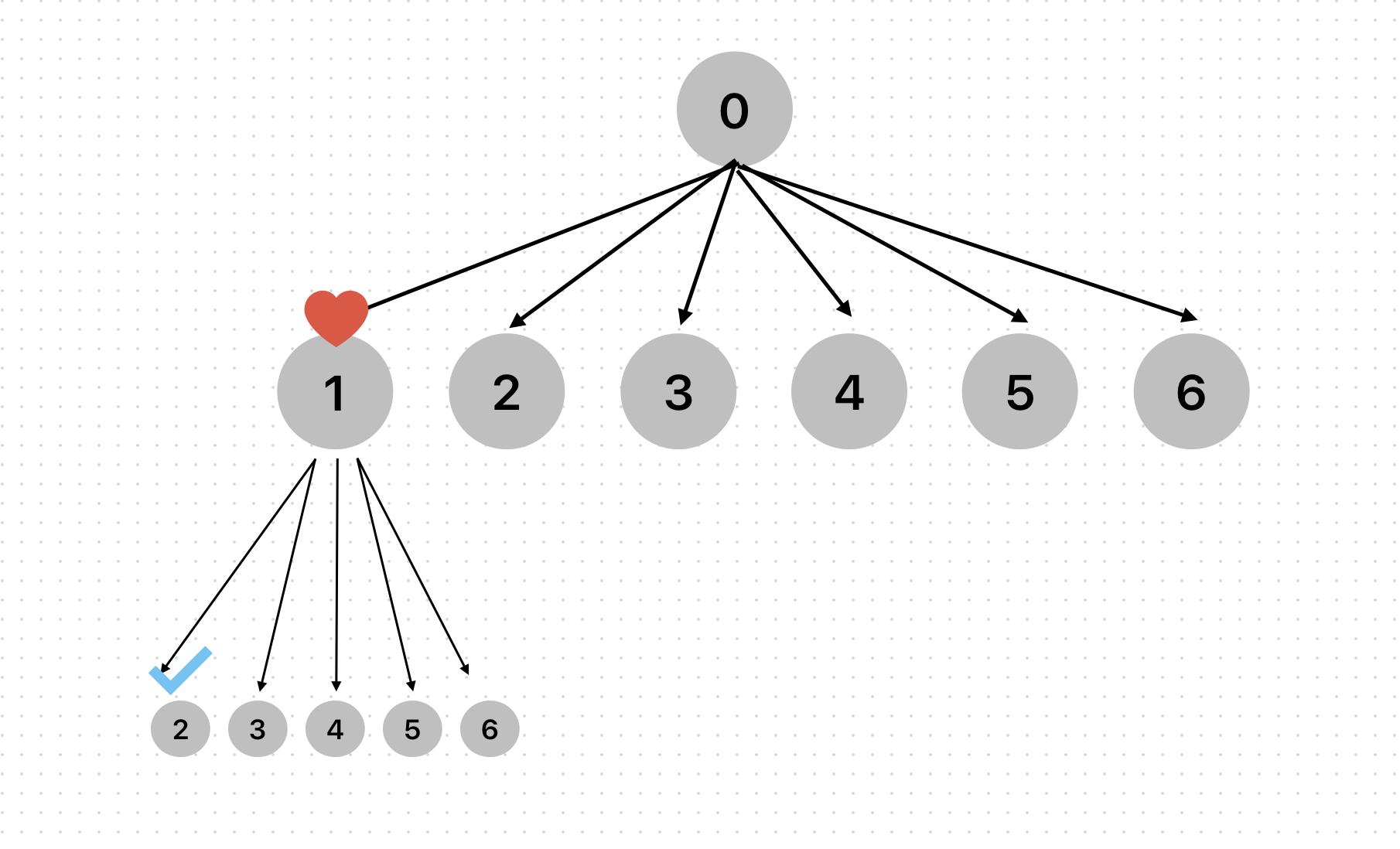
2는 방문이 완료되었으므로 다시 탐색해서는 안된다.
즉, for문에 추가되어야 하는 코드는 다음과 같다.

1. 현재 i값이 방문 표시가 되어 있는지 먼저 확인
2. 방문표시가 되어 있지 않다면 방문 표시를 하고 현재 i값을 ans에 저장한다.
3. 돌아 왔을 때 방문 표시를 해제한다.

방문 표시를 해제해 줘야 백트래킹 알고리즘이다. 밑으로 내려가면서 끝까지 찍고 다시 돌아오는 과정을 모두 수행하는게 백트래킹인데, 다시 돌아올려면 방문 표시를 해제해 줘야 한다. 다시 돌아오면서 이전에 저장해놓은 값들에는 방문하지 않은게 되기 때문이다.

이를 그대로 옮기면,

for(int i = 1; i <= n; i++){
	if(!visited[i]){
      visited[i] = true;
      ans[cnt] = i;
      dfs(i, cnt + 1);
      visited[i] = false;
    }
  }

이런식으로 모든 경우의 수를 순회할 수 있다.
전체 코드는 다음과 같다.

#include <bits/stdc++.h>

using namespace std;

int n, m;

int ans[9];
bool visited[9];

void dfs(int idx, int cnt) {
  if (cnt == m) {
    for (int i = 0; i < m; i++) {
      cout << ans[i] << ' ';
    }
    cout << '\n';
    return;
  }
  for (int i = 1; i <= n; i++) {
    if(!visited[i]){
      visited[i] = true;
      ans[cnt] = i;
      dfs(i, cnt + 1);
      visited[i] = false;
    }
  }
}

int main() {
  cin >> n >> m;
  dfs(0, 0);
}