[번역] Fundamentals of Data Visualization - 5 Directory of visualizations

원문 Fundamentals of Data Visualization

5 Directory of visualizations

이 챕터는 데이터를 시각화할 때 자주 사용되는 다양한 플롯과 차트들을 빠르게 시각적으로 살펴볼 수 있는 개요를 제공합니다.

5.1 Amounts

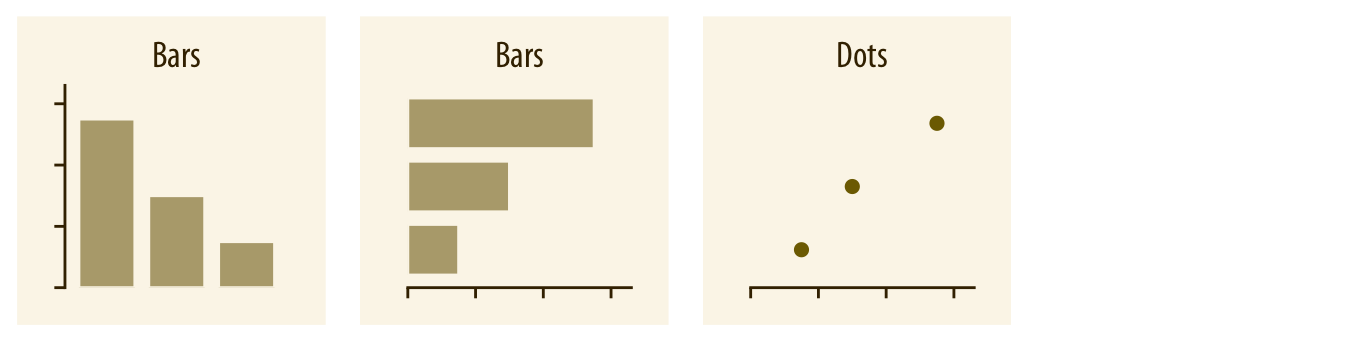
챕터 6 참조
가장 일반적인 방법으로는 막대 그래프를 사용하여 특정 범주에 대한 수치 값(즉, 양)을 시각화합니다. 막대는 세로 또는 가로로 배열될 수 있습니다. 하지만 막대 대신, 해당 막대가 끝나는 위치에 점을 배치하는 방법도 있습니다.

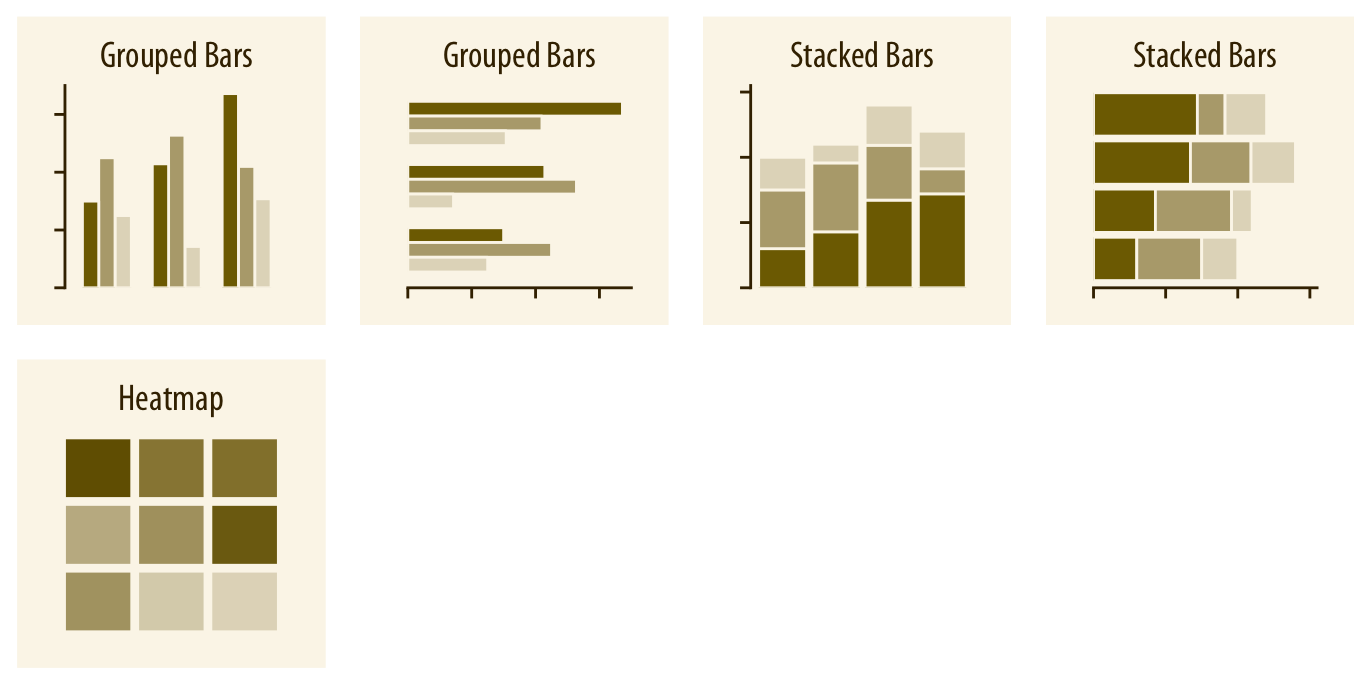
두 개 이상의 범주 집합에 대해 수치를 보여주고자 할 때는 막대를 그룹화하거나 쌓아 올리는 방법을 사용할 수 있습니다. 또한, 범주를 x축과 y축에 매핑하고, 색상을 통해 수치를 나타내는 히트맵을 사용할 수도 있습니다.

5.2 Distributions

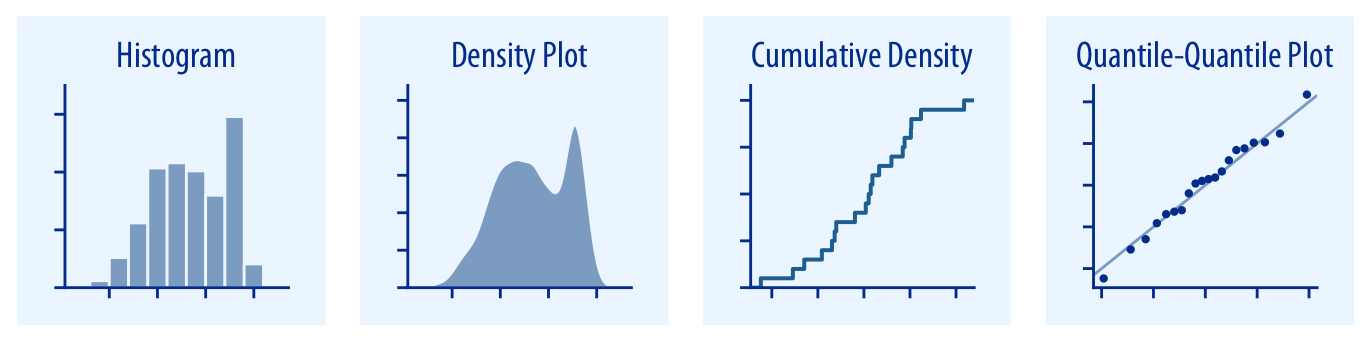
히스토그램과 밀도 플롯(챕터 7)은 분포를 가장 직관적으로 시각화할 수 있는 방법을 제공하지만, 둘 다 임의의 파라미터 선택이 필요하며, 잘못 해석될 수 있습니다. 누적 밀도와 분위-분위(q-q) 플롯(챕터 8)은 항상 데이터를 충실하게 표현하지만, 해석하기가 더 어려울 수 있습니다.

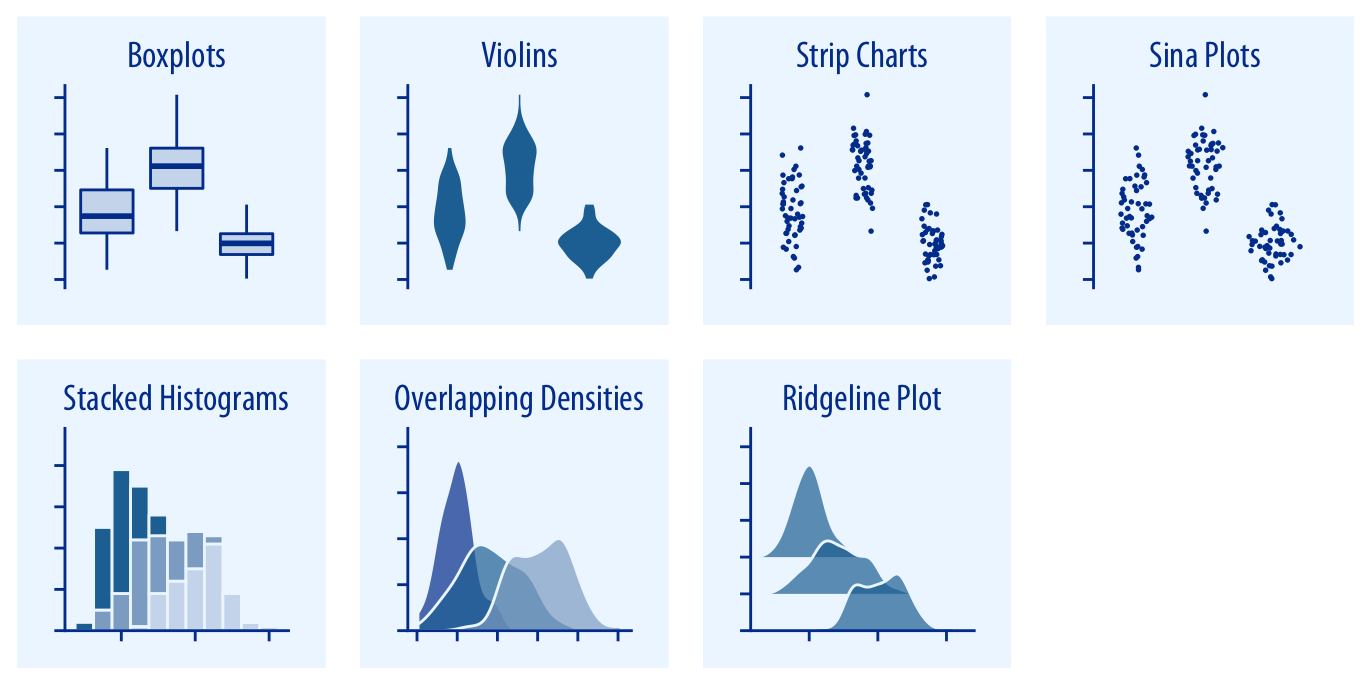
박스플롯, 바이올린 플롯, 스트립 차트, 그리고 시나 플롯은 여러 분포를 한 번에 시각화하거나, 분포 간의 전반적인 변화를 주로 관심을 가질 때 유용합니다(챕터 9.1 참조). 스택된 히스토그램과 겹쳐진 밀도 플롯은 적은 수의 분포를 더 깊이 비교할 수 있는 방법이지만, 스택된 히스토그램은 해석이 어려울 수 있어 가급적 피하는 것이 좋습니다(챕터 7.2 참조). 리지라인 플롯은 바이올린 플롯에 대한 유용한 대안이 될 수 있으며, 매우 많은 분포나 시간에 따른 분포 변화를 시각화할 때 종종 유용합니다(챕터 9.2 참조).

5.3 Proportions

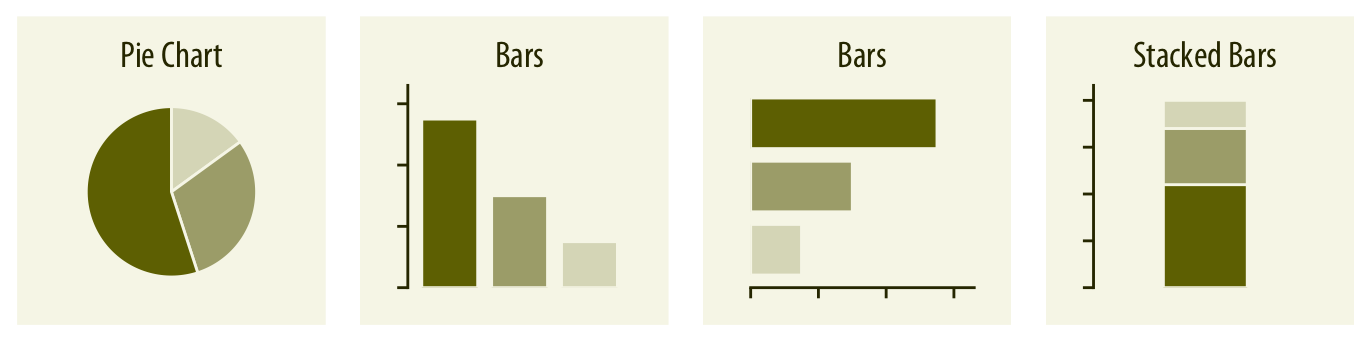
비율은 원형 차트, 나란히 배치된 막대, 또는 스택된 막대를 사용하여 시각화할 수 있습니다(챕터 10 참조). 수치 시각화의 경우처럼, 막대는 세로 또는 가로로 배열할 수 있습니다. 원형 차트는 개별 부분들이 전체를 이루고 있음을 강조하며, 단순한 분수를 강조할 때 효과적입니다. 그러나 개별 부분들은 나란히 배치된 막대에서 더 쉽게 비교할 수 있습니다. 스택된 막대는 하나의 비율 집합을 나타낼 때는 어색해 보일 수 있지만, 여러 비율 집합을 비교할 때 유용할 수 있습니다(아래 참조).

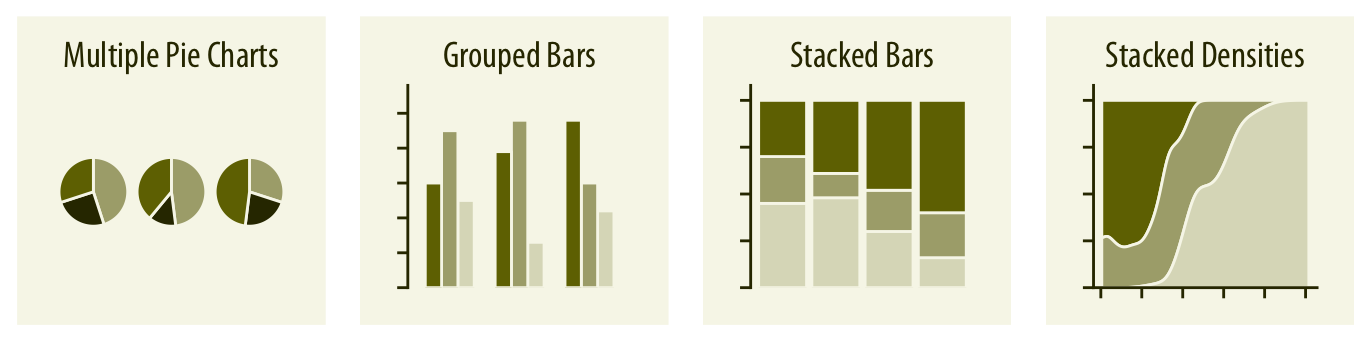
여러 비율 집합이나 조건에 따른 비율 변화를 시각화할 때, 원형 차트는 공간 효율이 낮고 관계를 흐리게 만들 수 있습니다. 그룹화된 막대는 비교하는 조건의 수가 적당할 때 효과적이며, 스택된 막대는 많은 수의 조건을 비교할 때 적합합니다. 비율이 연속적인 변수에 따라 변하는 경우에는 스택된 밀도 플롯(챕터 10 참조)이 적절한 선택입니다.

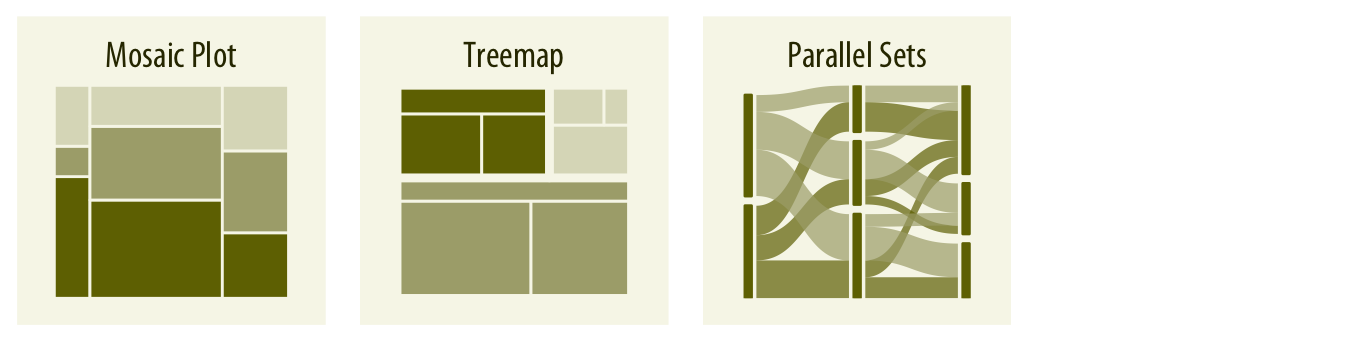
비율이 여러 그룹 변수에 따라 지정될 때, 모자이크 플롯, 트리맵, 또는 병렬 세트는 유용한 시각화 접근 방식입니다(챕터 11 참조). 모자이크 플롯은 하나의 그룹 변수의 모든 레벨이 다른 그룹 변수의 모든 레벨과 결합될 수 있다고 가정하지만, 트리맵은 이러한 가정을 하지 않습니다. 트리맵은 하나의 그룹 세분화가 다른 그룹의 세분화와 완전히 구분되더라도 잘 작동합니다. 병렬 세트는 그룹 변수의 수가 두 개 이상일 때, 모자이크 플롯이나 트리맵보다 더 나은 성능을 발휘합니다.

5.4 x–y relationships

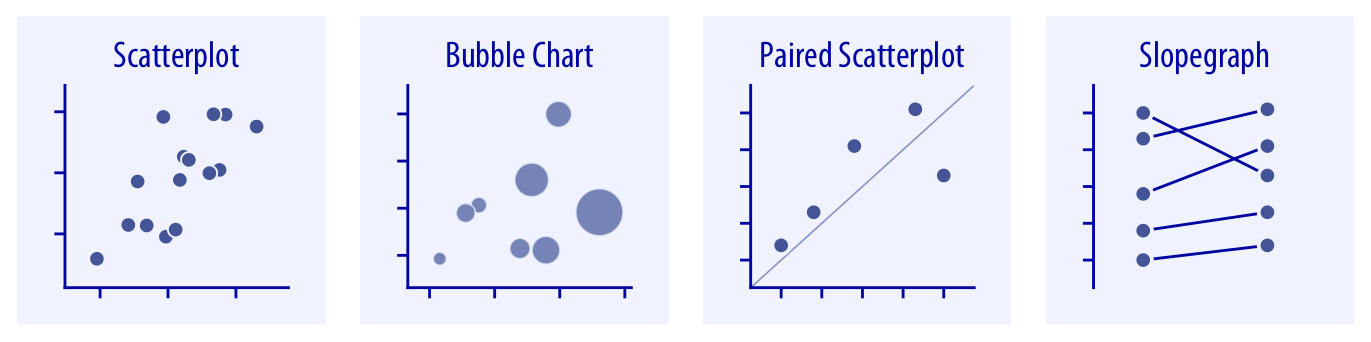
산점도는 하나의 수치형 변수를 다른 변수에 대해 보여주고자 할 때 전형적으로 사용하는 시각화 방법입니다(챕터 12.1 참조). 세 개의 수치형 변수가 있을 경우, 한 변수를 점의 크기로 매핑하여 버블 차트라는 산점도의 변형을 만들 수 있습니다. x축과 y축 변수의 단위가 동일한 쌍 데이터의 경우, 일반적으로 𝑥=𝑦를 나타내는 선을 추가하는 것이 도움이 됩니다(챕터 12.4 참조). 쌍 데이터는 또한 쌍의 점들을 직선으로 연결한 슬로프 그래프로도 표시할 수 있습니다(챕터 12.4 참조).

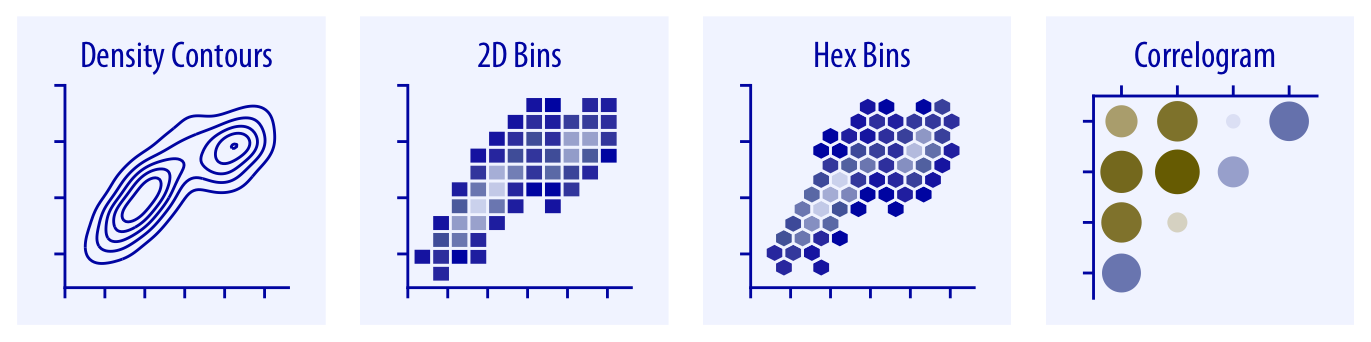
많은 수의 점이 있을 경우, 일반적인 산점도는 점들이 겹쳐져 유용한 정보를 제공하지 못할 수 있습니다. 이럴 때는 등고선, 2D 빈, 또는 헥스 빈을 사용한 대안적인 시각화 방법이 유용할 수 있습니다(챕터 18 참조). 반면, 두 개 이상의 변수를 시각화하고자 할 때는 기본적인 원시 데이터 대신 상관 계수를 코렐로그램의 형태로 플로팅하는 것을 선택할 수 있습니다(챕터 12.2 참조).

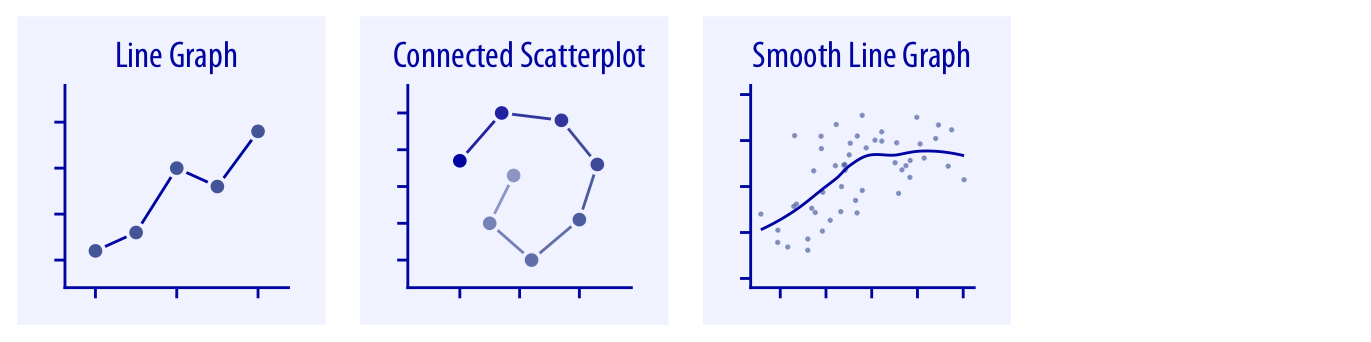
x축이 시간이나 치료 용량과 같은 엄격히 증가하는 양을 나타낼 때, 우리는 일반적으로 선 그래프를 그립니다(챕터 13 참조). 두 개의 반응 변수가 시간 순서에 따라 나타나는 경우, 먼저 산점도에서 두 반응 변수를 플로팅한 후, 인접한 시간 지점을 연결한 연결 산점도를 그릴 수 있습니다(챕터 13.3 참조). 더 큰 데이터셋에서의 추세를 나타내기 위해 부드러운 선을 사용할 수 있습니다(챕터 14 참조).

5.5 Geospatial data

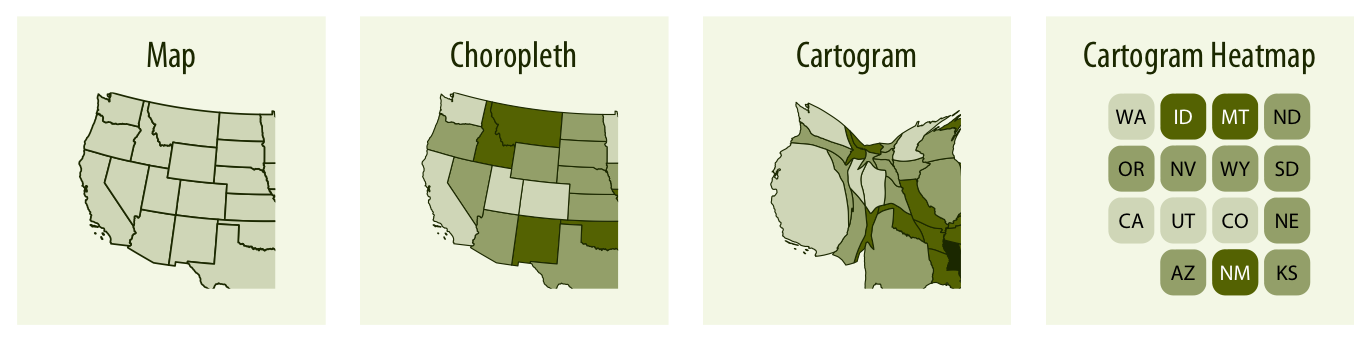
지리 데이터를 시각화하는 주요 방식은 지도를 사용하는 것입니다(챕터 15 참조). 지도는 지구상의 좌표를 평면에 투영하여, 지구상의 형태와 거리를 2D 표현에서 대략적으로 나타냅니다. 추가적으로, 데이터를 지도상의 다양한 지역에 색으로 표현하여, 해당 지역의 데이터 값을 시각화할 수 있습니다. 이러한 지도를 코로플레스라고 합니다(챕터 15.3 참조). 경우에 따라, 인구 수와 같은 다른 양에 따라 지역의 크기를 왜곡하거나, 각 지역을 사각형으로 단순화하는 것이 도움이 될 수 있습니다. 이러한 시각화는 카르토그램이라고 합니다.

5.6 Uncertainty

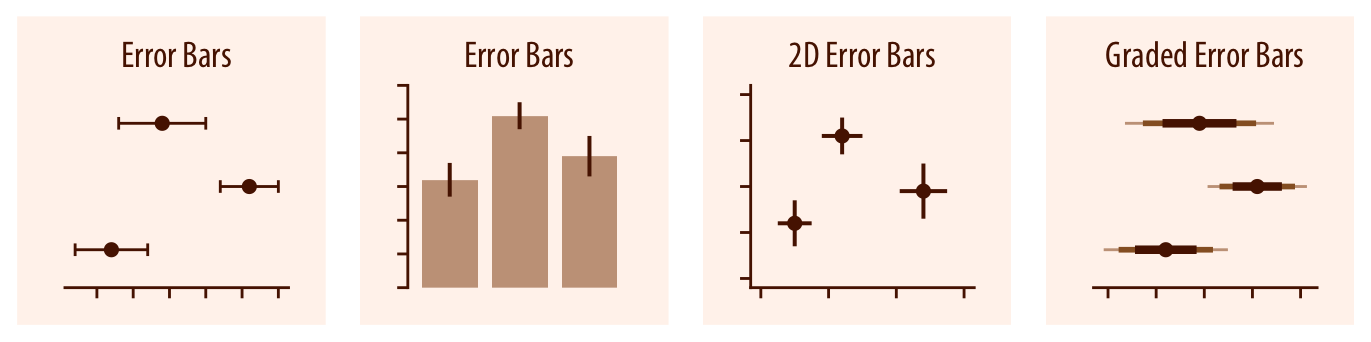
오차 막대는 어떤 추정치나 측정치에 대해 가능한 값의 범위를 나타내기 위해 사용됩니다. 이들은 추정치나 측정치를 나타내는 기준점에서 수평 및/또는 수직으로 확장됩니다(챕터 16 참조). 기준점은 점이나 막대 등 다양한 방식으로 표시될 수 있습니다. 그라데이션 오차 막대는 여러 범위를 동시에 보여주며, 각 범위는 다른 신뢰 수준을 나타냅니다. 이들은 사실상 서로 다른 선 두께로 그려진 여러 개의 오차 막대가 겹쳐진 형태입니다.

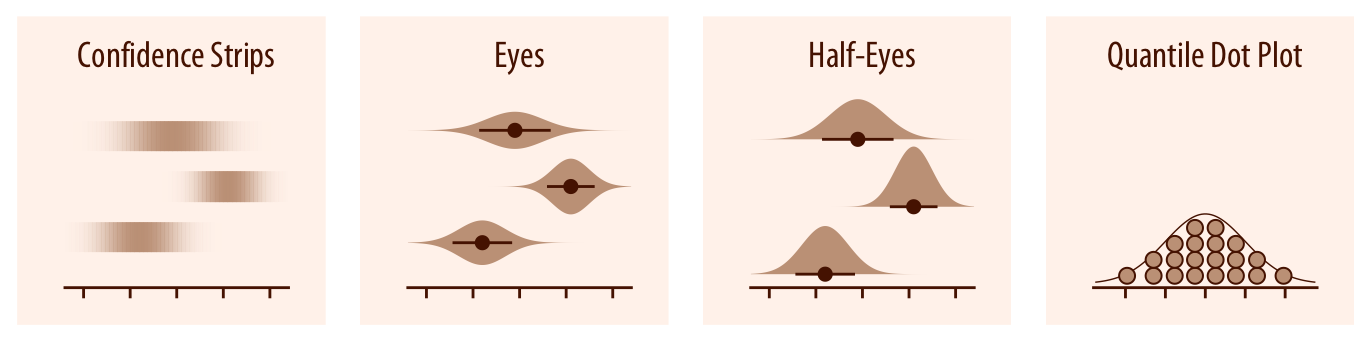
오차 막대나 그라데이션 오차 막대보다 더 상세한 시각화를 위해, 실제 신뢰 구간이나 사후 분포를 시각화할 수 있습니다(챕터 16 참조). 신뢰 스트립은 불확실성을 명확하게 시각화하지만, 정확하게 읽기는 어렵습니다. 아이 플롯과 하프 아이 플롯은 각각 바이올린 플롯과 리지라인 플롯을 결합하여 오차 막대와 분포를 시각화하는 접근 방식을 결합한 것입니다. 이를 통해 특정 신뢰 수준의 정확한 범위와 전체 불확실성 분포를 모두 보여줍니다. 분위 점 플롯은 불확실성 분포를 시각화하는 대안으로 사용할 수 있습니다(챕터 16.1 참조). 분위 점 플롯은 분포를 이산 단위로 보여주기 때문에, 바이올린이나 리지라인 플롯이 보여주는 연속적인 분포보다 정확도는 떨어지지만, 읽기 쉽다는 장점이 있습니다.

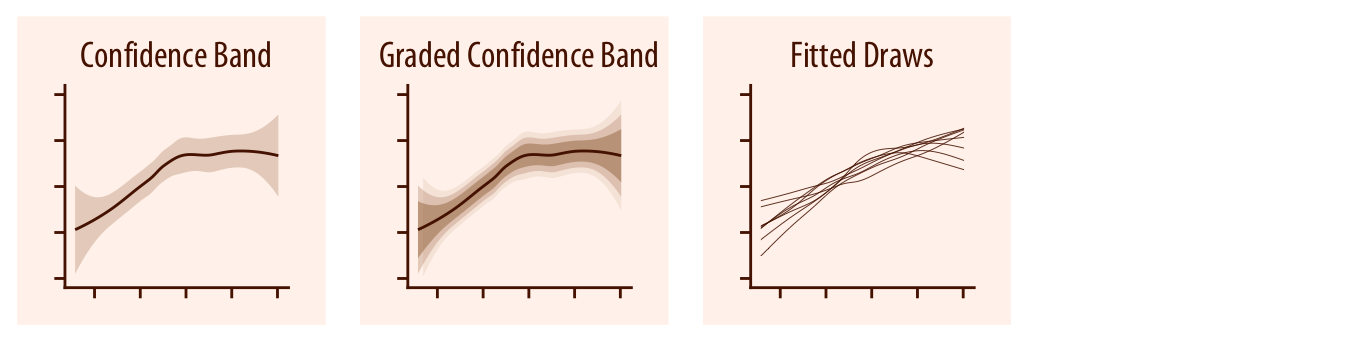
스무스 라인 그래프에서, 오차 막대에 해당하는 것은 신뢰 밴드입니다(챕터 16.3 참조). 신뢰 밴드는 특정 신뢰 수준에서 선이 통과할 수 있는 값의 범위를 보여줍니다. 오차 막대의 경우와 마찬가지로, 여러 신뢰 수준을 동시에 보여주는 그라데이션 신뢰 밴드를 그릴 수 있습니다. 또한, 신뢰 밴드 대신 또는 신뢰 밴드와 함께 개별 맞춤 드로우를 시각화할 수도 있습니다.