[번역] Fundamentals of Data Visualization -14 Visualizing trends

14 Visualizing trends

주로 산점도(Chapter 12)나 시계열(Chapter 13)에서 개별 데이터 포인트가 어디에 위치하는지보다 데이터의 전체적인 흐름에 더 관심이 있을 때가 많습니다. 추세를 실제 데이터 포인트 위나 그 대신에 그려줌으로써, 보통 직선이나 곡선의 형태로 나타내어 독자가 데이터의 주요 특징을 즉시 파악할 수 있도록 하는 시각화를 만들 수 있습니다.

추세를 파악하는 데에는 두 가지 기본적인 접근 방식이 있습니다. 첫 번째는 이동 평균과 같은 방법으로 데이터를 평활화(smoothing)하는 것이고, 두 번째는 정의된 함수 형태로 곡선을 맞춘 후에 그 곡선을 그리는 것입니다. 데이터셋에서 추세를 파악한 후에는 그 추세에서의 편차를 구체적으로 살펴보거나, 데이터를 기본 추세, 주기적 요소, 그리고 에피소드적 요소 또는 무작위 잡음과 같은 여러 구성 요소로 나누어 보는 것이 유용할 수 있습니다.

14.1 Smoothing

2008년 금융 위기 직후인 2009년을 살펴보고 있습니다. 2009년 첫 3개월 동안 시장은 2400포인트 이상(~27%) 하락했으며, 그 후에는 연말까지 서서히 회복되었습니다. 이러한 장기적인 추세를 시각화하면서 단기적인 변동은 덜 강조하는 방법을 생각해볼 수 있습니다.

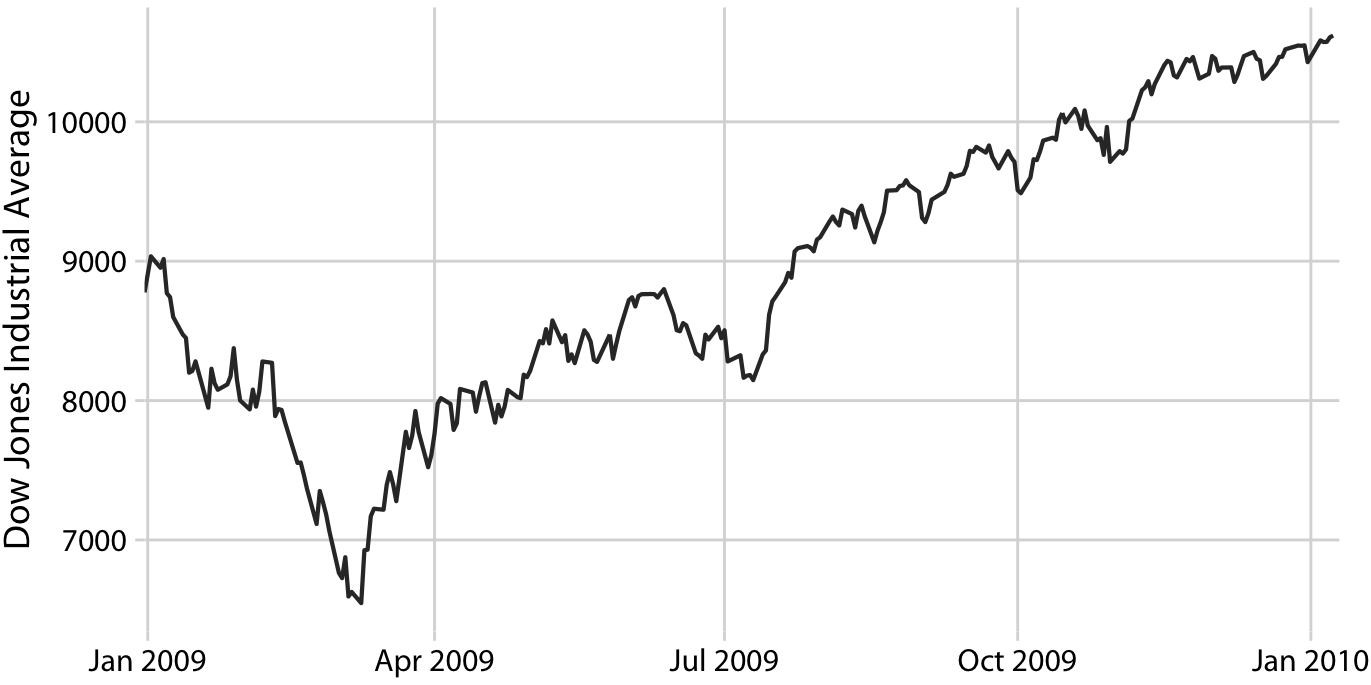
평활화(smoothing)는 데이터에서 중요 패턴을 포착하면서도 관련 없는 세부 사항이나 잡음을 제거하는 함수 생성 과정입니다. 금융 분석가들은 주식 시장 데이터를 평활화하기 위해 주로 이동 평균(moving averages)을 계산합니다. 이동 평균을 생성하려면 먼저 특정 시간 창을 선택합니다. 예를 들어, 시계열의 첫 20일 동안의 평균 가격을 계산한 다음, 이 시간 창을 하루씩 이동하면서 새로운 평균을 계산합니다. 이렇게 하면 평균 가격의 새로운 시계열이 생성됩니다.

이 이동 평균 시계열을 플로팅할 때, 각 시간 창의 평균을 어느 시점과 연관시킬지를 결정해야 합니다. 금융 분석가들은 보통 각 평균을 해당 시간 창의 끝에 위치시키는데, 이는 원래 데이터보다 뒤처진 곡선을 생성합니다. 더 큰 시간 창을 사용할수록 이러한 지연이 더욱 심해집니다. 반면, 통계학자들은 평균을 시간 창의 중심에 위치시켜, 원래 데이터와 완벽하게 겹치는 곡선을 생성합니다.

금융 분석가들은 종종 과거 데이터를 기반으로 미래를 예측하기 때문에 후행 곡선을 선호할 수 있습니다. 통계학자들은 데이터의 패턴을 정확하게 포착하는 데 더 중점을 두기 때문에, 중앙에 위치한 곡선을 선호합니다.

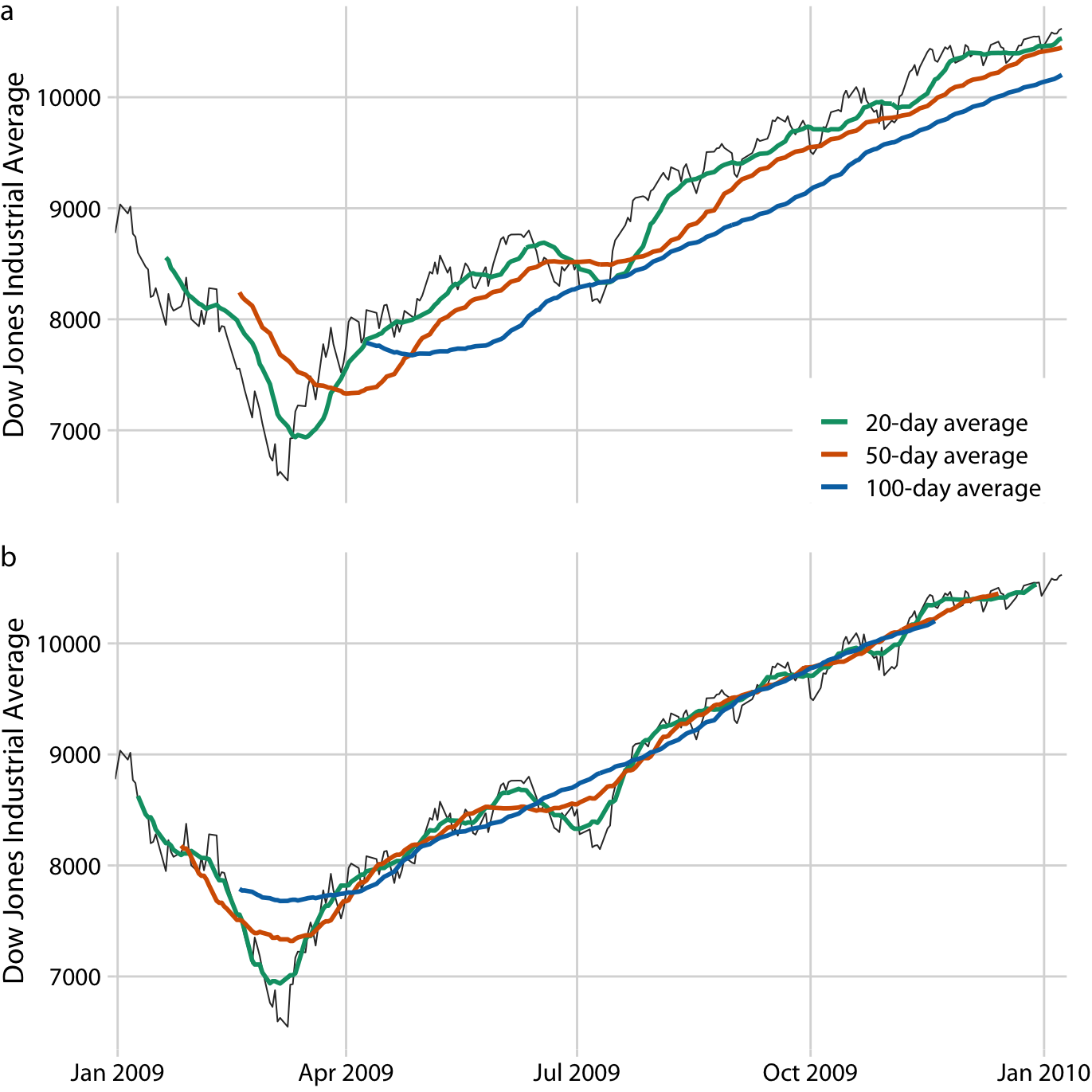
이동 평균은 가장 간단한 평활화 방법이지만, 몇 가지 명백한 한계가 있습니다. 첫째, 평활화된 곡선은 원래 곡선보다 짧아집니다. 이는 평활화 과정에서 곡선의 시작과 끝 부분이 손실되기 때문입니다. 시간 창이 커질수록 평활화된 곡선은 더 짧아집니다. 둘째, 큰 시간 창을 사용하더라도 이동 평균이 반드시 부드럽지는 않습니다. 작은 융기나 흔들림이 발생할 수 있는데, 이는 평균 창에 들어오거나 나가는 개별 데이터 포인트에 의해 발생합니다. 창의 모든 데이터 포인트가 동일하게 가중되기 때문에, 창의 경계에 있는 개별 데이터 포인트가 평균에 가시적인 영향을 미칠 수 있습니다.

통계학자들은 이러한 이동 평균의 단점을 완화하기 위해 더 복잡하고 계산 비용이 많이 드는 평활화 방법들을 개발했습니다. 그 중 널리 사용되는 방법 중 하나가 LOESS(Locally Estimated Scatterplot Smoothing)입니다. 이 방법은 데이터의 하위 집합에 저차 다항식을 맞추며, 각 하위 집합의 중앙에 있는 점에 더 많은 가중치를 부여하여 이동 평균보다 훨씬 부드러운 결과를 얻습니다.

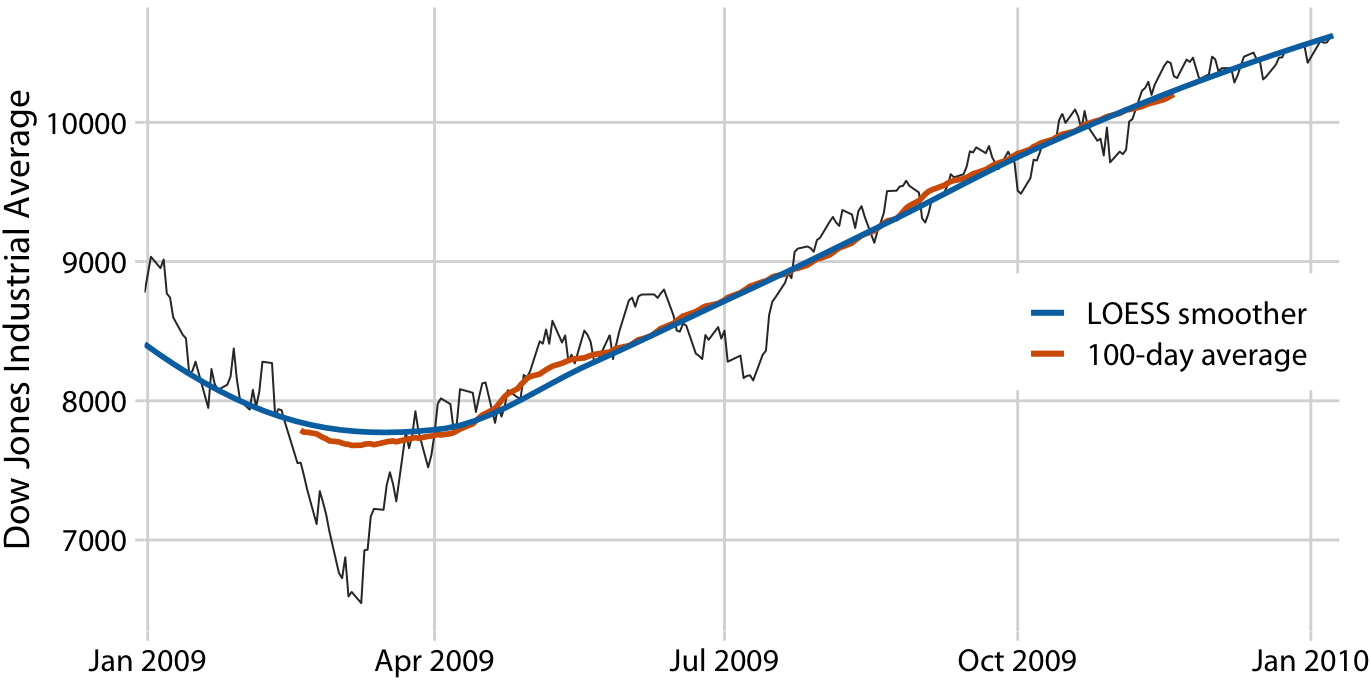
두 곡선 모두 전체적인 추세는 거의 동일하지만, LOESS 곡선은 훨씬 부드럽고 데이터 전체 범위에 걸쳐 확장된다는 점에서 차이가 있습니다. 이는 LOESS의 주요 장점 중 하나로, 데이터의 경계 부분에서도 부드러운 추세선을 제공할 수 있습니다.

또한, LOESS는 시계열 데이터에 국한되지 않고 임의의 산점도에도 적용될 수 있습니다. LOESS 선은 가격이 저렴한 자동차(20,000달러 이하)의 경우 탱크 용량이 가격과 거의 선형적으로 증가하지만, 더 비싼 자동차에서는 이 관계가 완만해진다는 것을 보여줍니다. 약 20,000달러 이상의 가격대에서는 더 비싼 자동차를 구매하더라도 더 큰 연료 탱크를 얻을 수 없다는 결론을 내릴 수 있습니다.

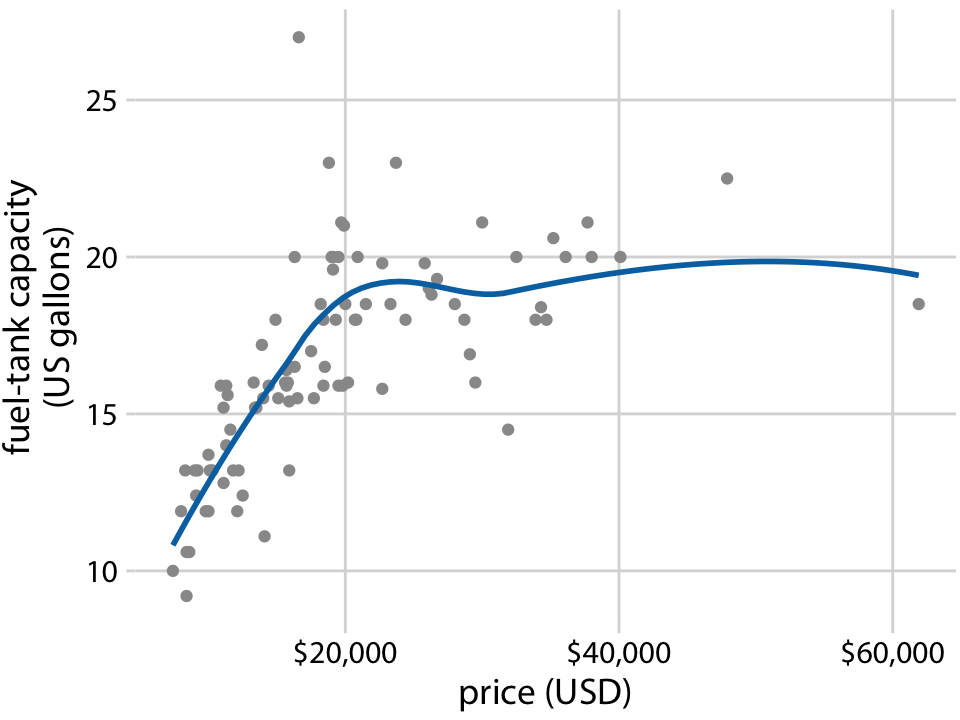
LOESS는 데이터를 부드럽게 만들어주는 매우 인기 있는 방법으로, 인간의 눈에 자연스럽게 보이는 결과를 만들어내는 경향이 있습니다. 하지만 LOESS는 많은 개별 회귀 모델을 적합시켜야 하기 때문에, 특히 대규모 데이터셋에서는 계산 속도가 느려질 수 있습니다. 이는 현대 컴퓨팅 장비에서도 성능상의 부담이 될 수 있습니다.

이에 대한 대안으로 스플라인 모델이 제시됩니다. 스플라인은 조각별 다항 함수로, 유연하면서도 항상 부드럽게 보이는 특성을 가지고 있습니다. 스플라인을 사용할 때는 knot(매듭)이라는 용어를 접하게 되는데, 이는 개별 스플라인 세그먼트의 끝점을 의미합니다. 예를 들어, k 개의 세그먼트를 가진 스플라인을 적합시키려면 k+1 개의 매듭을 지정해야 합니다. 스플라인 적합은 계산 효율성이 높으며, 특히 매듭의 수가 많지 않은 경우에는 더욱 그렇습니다.

그러나 스플라인에는 단점도 있습니다. 가장 큰 문제는 스플라인의 종류가 매우 다양하다는 점입니다. 예를 들어, 큐빅 스플라인(cubic splines), B-스플라인(B-splines), 얇은 판 스플라인(thin-plate splines), 가우시안 프로세스 스플라인(Gaussian process splines) 등 많은 종류가 있으며, 어떤 것을 선택해야 할지 명확하지 않을 수 있습니다. 특정 유형의 스플라인과 매듭의 수에 따라 동일한 데이터에 대해 매우 다른 평활화 함수가 생성될 수 있습니다.

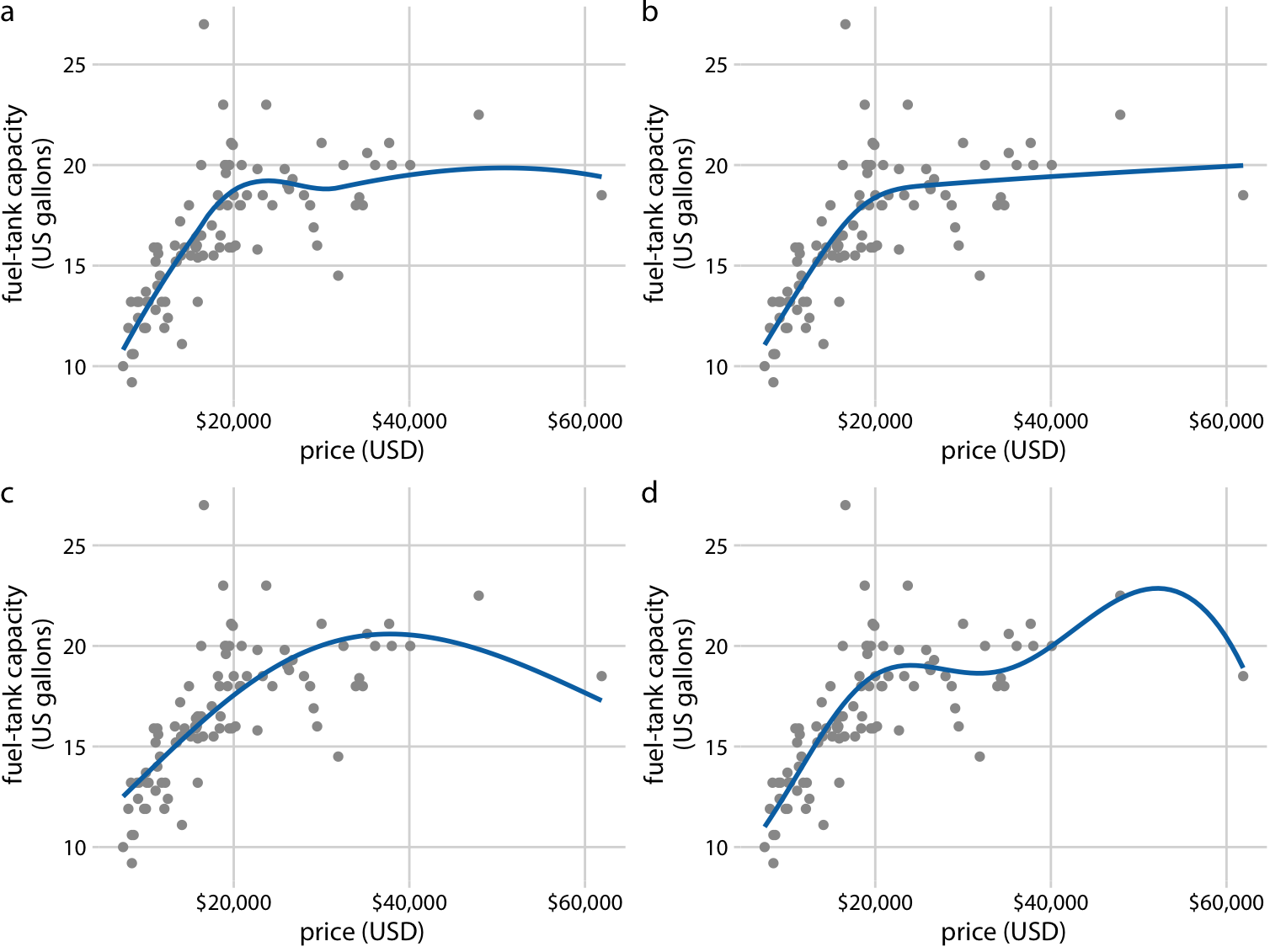
LOESS 평활화 (a): 이전에 언급된 것처럼, 이 방법은 데이터의 지역적인 회귀 분석을 사용하여 부드러운 곡선을 생성합니다.
cubic regression splines with 5 knots (b): 큐빅 스플라인은 각 구간에서 3차 다항식을 사용하여 곡선을 부드럽게 만듭니다.
thin-plate regression spline with 3 knots (c): 이 스플라인은 구간 사이의 매끄러움을 최적화하면서도 유연성을 유지하려고 합니다.
Gaussian process spline with 6 knots (d): 가우시안 프로세스를 기반으로 한 이 방법은 특정 매개변수와 함께 유연한 평활화를 제공합니다.

14.2 Showing trends with a defined functional form

일반적인 평활화 기법의 예측 불확실성을 극복하기 위해, 데이터에 적합한 특정 함수 형태를 사용하여 곡선을 맞추는 것이 더 나은 방법일 수 있습니다. 이러한 방법은 매개변수가 명확한 의미를 가지며, 데이터를 더 잘 설명할 수 있습니다.

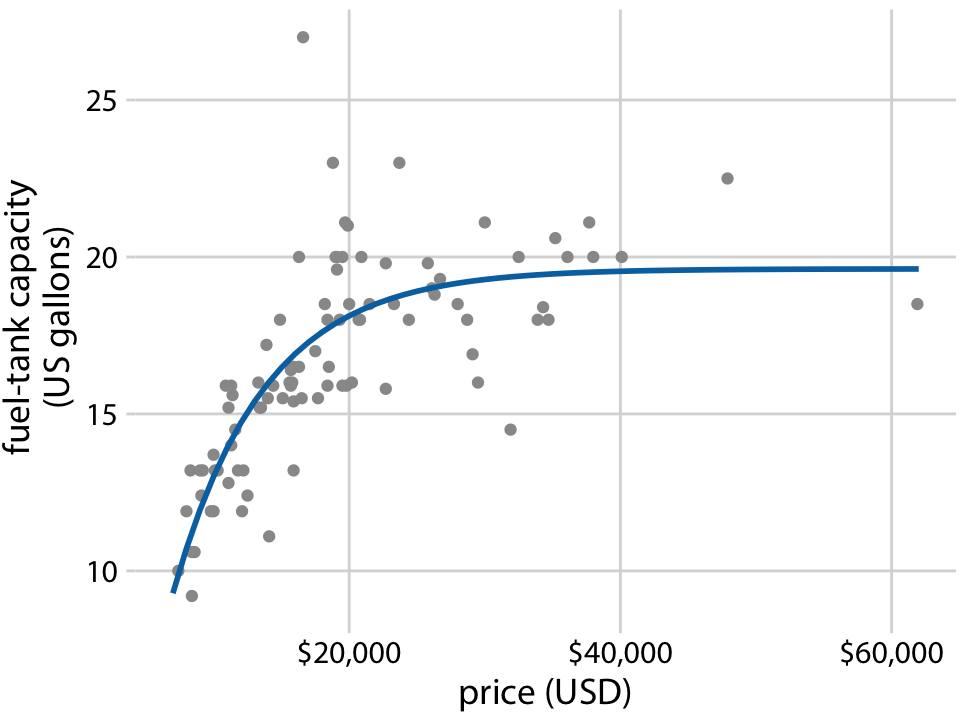
예를 들어, 연료 탱크 데이터의 경우 처음에는 선형으로 증가하다가 일정 값에 도달하면 평탄해지는 곡선이 필요합니다. 이를 표현할 수 있는 함수는 다음과 같습니다:

이 함수가 이전에 고려했던 평활화 방법 중 어느 것과도 비슷하게 데이터를 잘 맞추는 것을 보여줍니다.

또한, 단순한 직선 모델도 여러 상황에서 유용하게 사용할 수 있는 함수 형태로 소개되고 있습니다. 이 함수는 다음과 같이 표현됩니다:

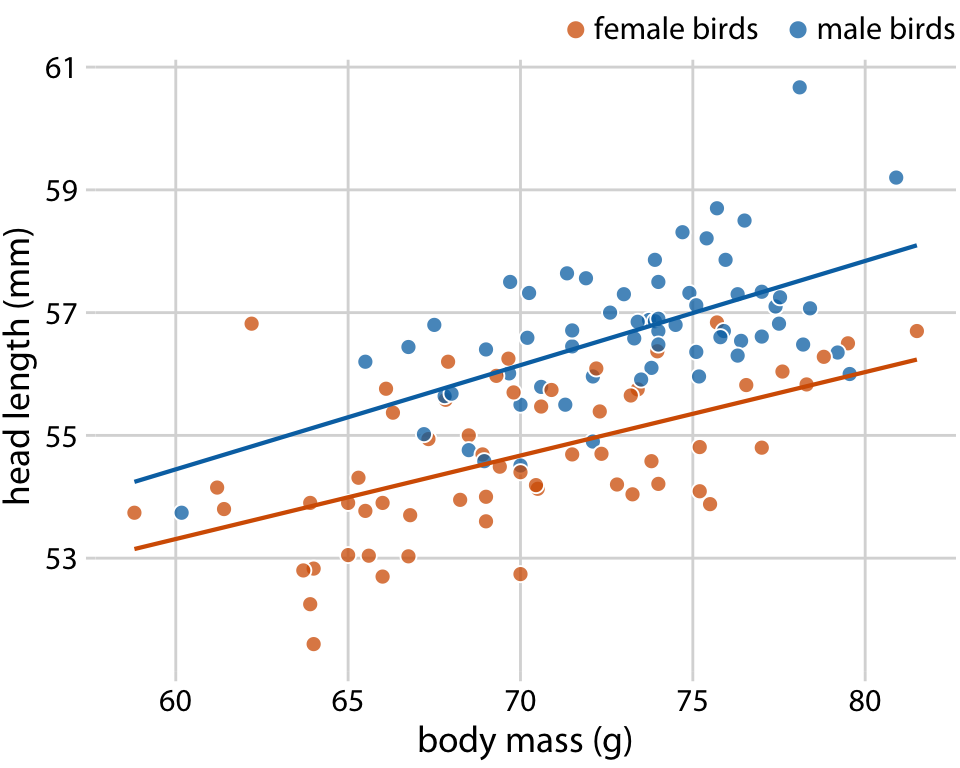
두 변수 간의 관계가 대략적으로 선형일 때, 이 단순한 직선 모델이 매우 효과적입니다. 실세계 데이터셋에서 이러한 선형 관계는 놀라울 정도로 흔합니다. 예를 들어, Chapter 12에서 blue jays 새의 머리 길이와 체중 사이의 관계가 남녀 모두에서 대략적으로 선형 관계를 보이는 것으로 논의되었습니다. 이러한 선형 추세선을 산점도에 그려주면, 독자가 데이터 내의 추세를 더 쉽게 파악할 수 있습니다

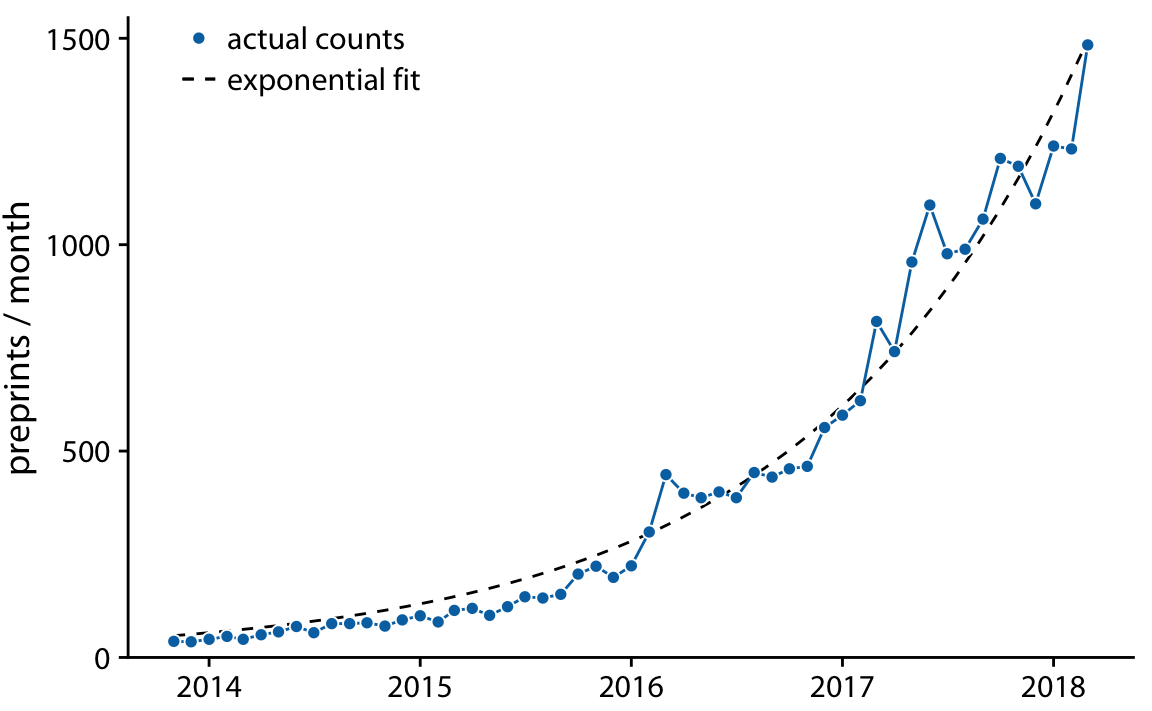
하지만 데이터가 비선형 관계를 보이는 경우, 적절한 함수 형태를 추정해야 합니다. 이때 축을 변환하여 선형 관계가 나타나도록 할 수 있습니다. 예를 들어, Chapter 12에서 논의된 bioRxiv에 대한 월별 제출 건수 데이터를 다시 살펴보면, 매달 제출 건수의 증가가 이전 달 제출 건수에 비례한다면, 즉 매달 고정된 비율로 제출 건수가 증가한다면, 이 관계는 지수 함수 형태를 따르게 됩니다.

이 가정이 bioRxiv 데이터에 잘 맞는 것으로 보이며, 지수 함수 형태의 곡선 y=A⋅exp(mx)가 bioRxiv 제출 데이터에 잘 맞습니다.

이러한 분석은 비선형 관계를 가진 데이터에서 축 변환이나 적절한 함수 형태를 사용하여 데이터를 더 잘 설명하고 해석할 수 있는 방법을 제시하고 있습니다.

데이터가 지수 함수 형태일 때, y=A⋅exp(mx), y 값을 로그 변환하면 선형 관계로 변환할 수 있습니다. 로그 변환을 통해 변환된 식은 다음과 같습니다:

따라서, y 값을 로그 변환하여 플로팅하거나 로그 y 축을 사용하여 데이터를 플로팅하면 선형 관계를 찾는 것이 데이터가 지수 성장(exponential growth)을 보이는지 여부를 판단하는 좋은 방법입니다. 실제로, bioRxiv 제출 건수 데이터에서 로그 y 축을 사용하면 선형 관계를 얻을 수 있습니다.

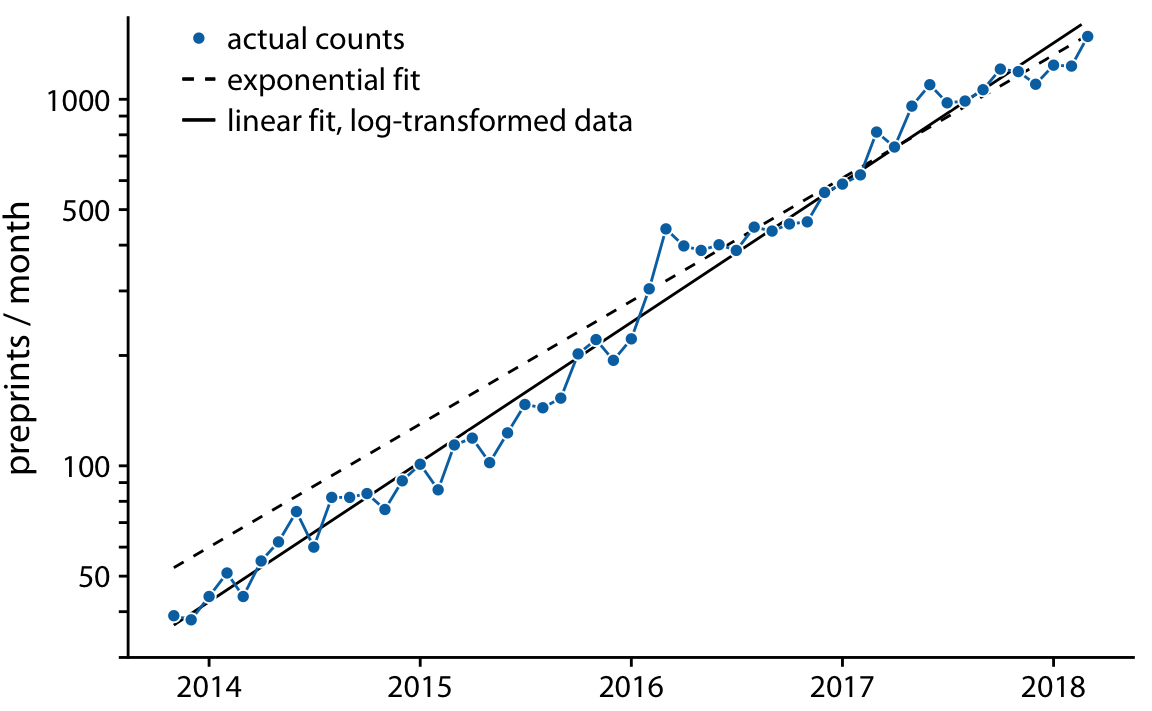
지수 적합선과 로그 변환된 데이터에 대한 선형 적합선을 함께 보여줍니다. 두 적합선은 유사하지만 완전히 동일하지는 않습니다. 특히, 점선으로 표시된 지수 적합선의 기울기가 약간 어긋나 있는 것을 볼 수 있습니다. 이 선은 시계열의 절반 동안 개별 데이터 포인트 위에 일정하게 놓여 있습니다. 이는 지수 적합의 일반적인 문제입니다. 데이터 값이 큰 경우, 그 데이터 포인트와 적합된 곡선 간의 제곱 편차가 매우 커지며, 작은 데이터 값의 편차는 전체 최소 자승합에 거의 기여하지 않게 됩니다. 그 결과, 적합된 선이 작은 데이터 값에 대해 과대 혹은 과소 평가하는 경우가 발생할 수 있습니다. 이러한 이유로, 지수 적합 대신 로그 변환된 데이터에 선형 적합을 사용하는 것이 일반적으로 더 낫습니다.

14.3 Detrending and time-series decomposition

어떤 시계열에서 장기적인 추세가 뚜렷하게 나타나는 경우, 이 추세를 제거하여 주목할 만한 편차를 강조하는 것이 유용할 수 있습니다. 이를 디트렌딩(detrending)이라고 합니다.

장기간 동안 주택 가격은 일반적으로 인플레이션과 비슷한 연간 성장률을 보입니다. 그러나 이 추세에 주택 시장의 버블이 겹쳐지면서 심한 붐과 버스트 사이클을 겪기도 합니다. 네 개의 미국 주에 대한 실제 주택 가격 지수와 그 장기적인 추세를 보여줍니다. 1980년부터 2017년까지 캘리포니아는 1990년과 2000년대 중반에 두 번의 버블을 겪었고, 네바다는 2000년대 중반에 한 번의 버블을 경험했습니다. 반면, 텍사스와 웨스트 버지니아의 주택 가격은 해당 기간 동안 장기적인 추세를 비교적 일관되게 따랐습니다. 주택 가격이 퍼센트 단위로 증가하는 경향이 있기 때문에, 로그 y축을 사용했습니다. 이 직선들은 캘리포니아의 연간 4.7% 가격 증가와 네바다, 텍사스, 웨스트 버지니아의 각각 연간 2.8% 가격 증가를 나타냅니다.

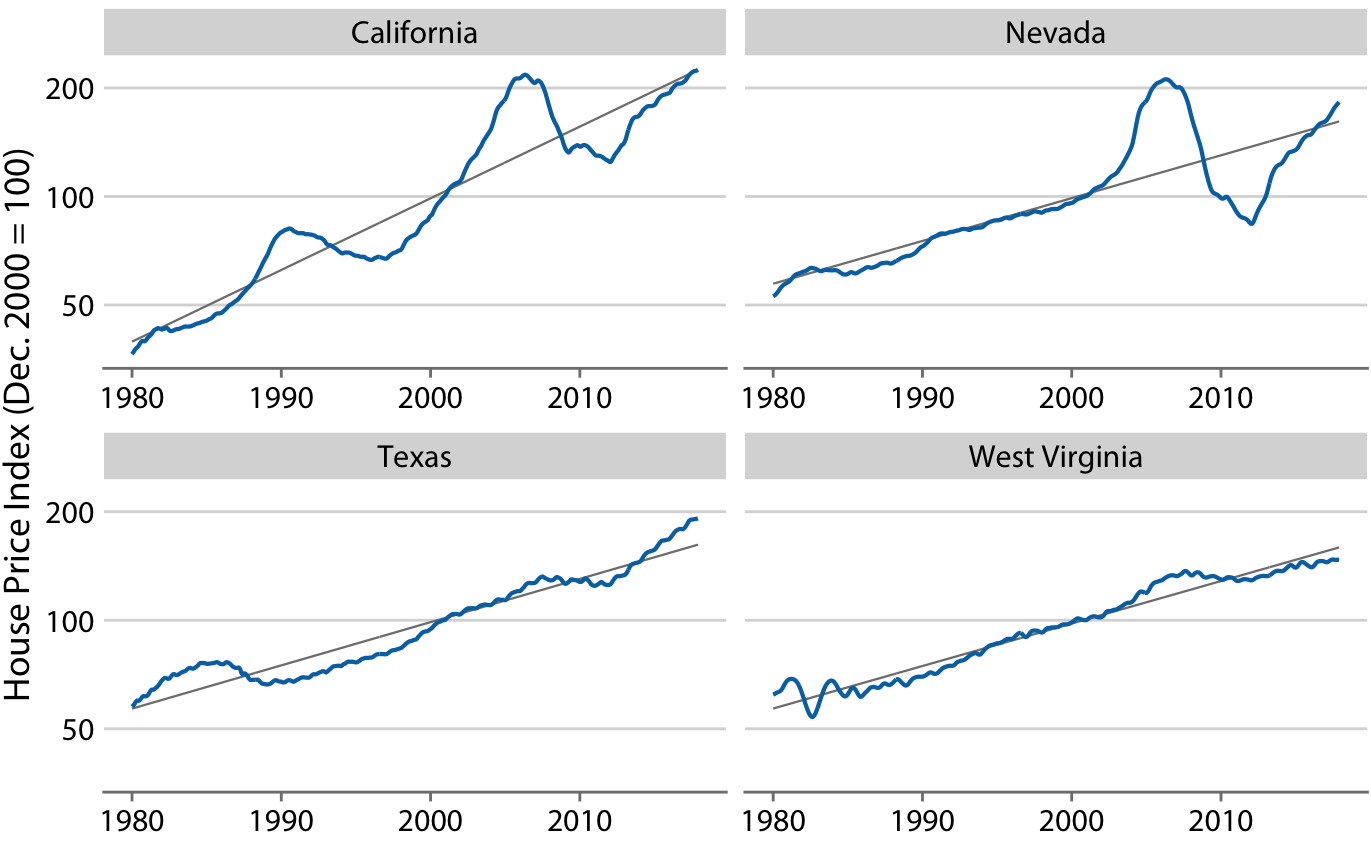
디트렌딩은 주택 가격 지수에서 장기적인 추세를 제거하여 주택 시장의 거품과 같은 비정상적인 변동을 강조하는 기법입니다. 이를 위해 각 시점의 실제 가격 지수를 해당 시점의 장기 추세 값으로 나누어줍니다. 시각적으로는 파란색 선에서 회색 선을 빼는 것처럼 보입니다.

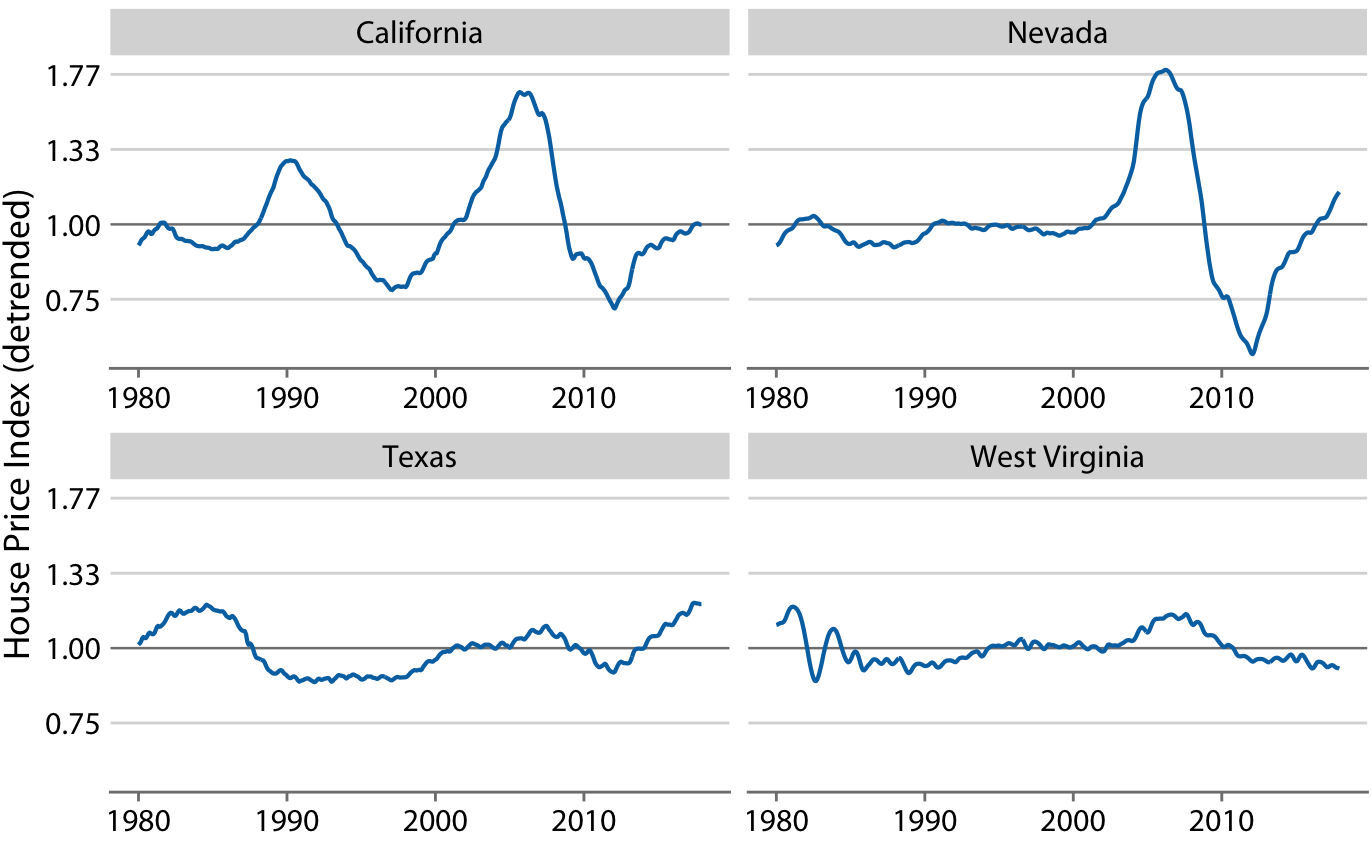
이 시각화를 통해 캘리포니아가 1990년대와 2000년대 중반에 두 번의 주택 거품을 경험했다는 것을 알 수 있습니다. 이 버블은 실제 주택 가격이 장기적인 추세에서 크게 벗어났을 때 나타나는 급격한 상승과 그 후의 하락으로 확인할 수 있습니다. 유사하게, 네바다는 2000년대 중반에 하나의 주택 거품을 경험했으며, 텍사스와 웨스트 버지니아는 거의 주택 거품을 경험하지 않았음을 알 수 있습니다.

단순한 디트렌딩 외에도, 시계열 데이터를 여러 개의 뚜렷한 구성 요소로 분해할 수 있습니다. 이러한 구성 요소의 합은 원래의 시계열 데이터를 복구합니다. 일반적으로, 장기적인 추세 외에도 시계열을 형성하는 세 가지 주요 구성 요소가 있습니다:

랜덤 노이즈(random noise): 이는 작은, 불규칙한 상하 변동을 일으킵니다.

고유한 외부 이벤트(unique external events): 이는 시계열에 뚜렷한 영향을 미치는 사건으로, 주택 거품과 같은 현상입니다.

주기적 변동(cyclical variations): 예를 들어, 외부 온도는 일일 주기 변동을 보입니다. 온도가 가장 높은 시간은 오후 초반이며, 가장 낮은 시간은 이른 아침입니다. 외부 온도는 또한 연간 주기 변동을 보이며, 봄에는 상승하고 여름에 최고점을 찍고, 가을에는 하락하여 겨울에 최저점에 도달합니다.

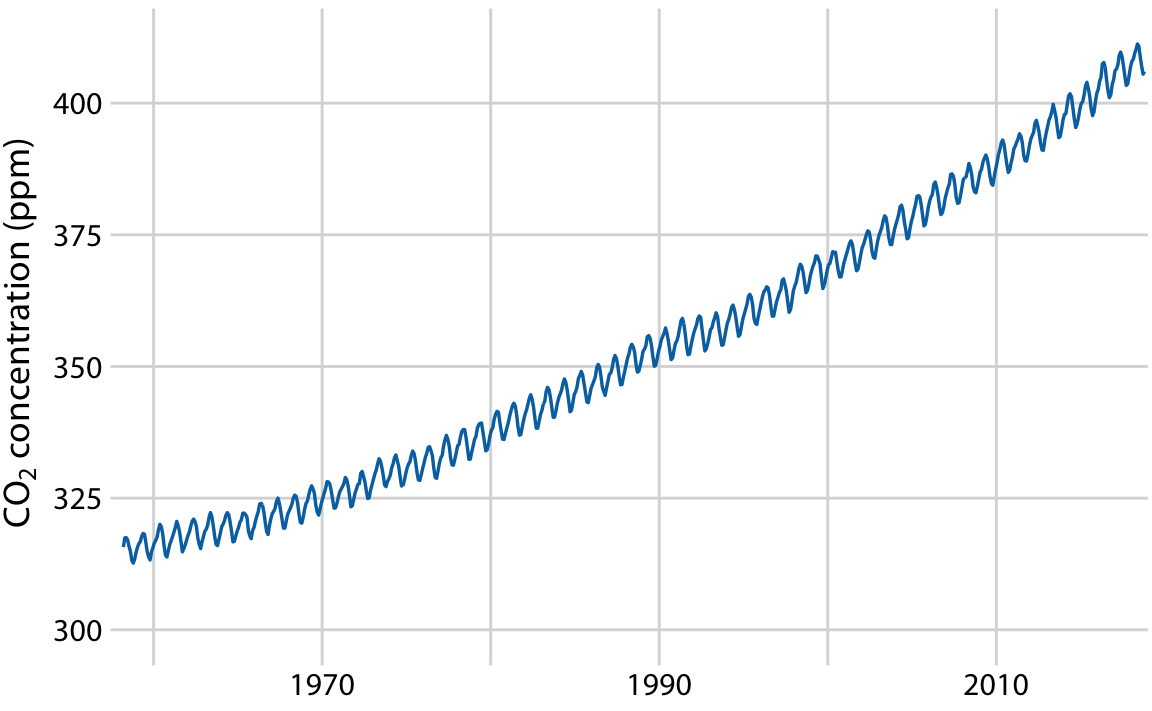
이 곡선은 대기 중 이산화탄소(CO2) 농도의 변화를 시간에 따라 나타낸 것입니다. 장기적인 추세, 계절 변동, 나머지 구성 요소로 분해할 수 있습니다.

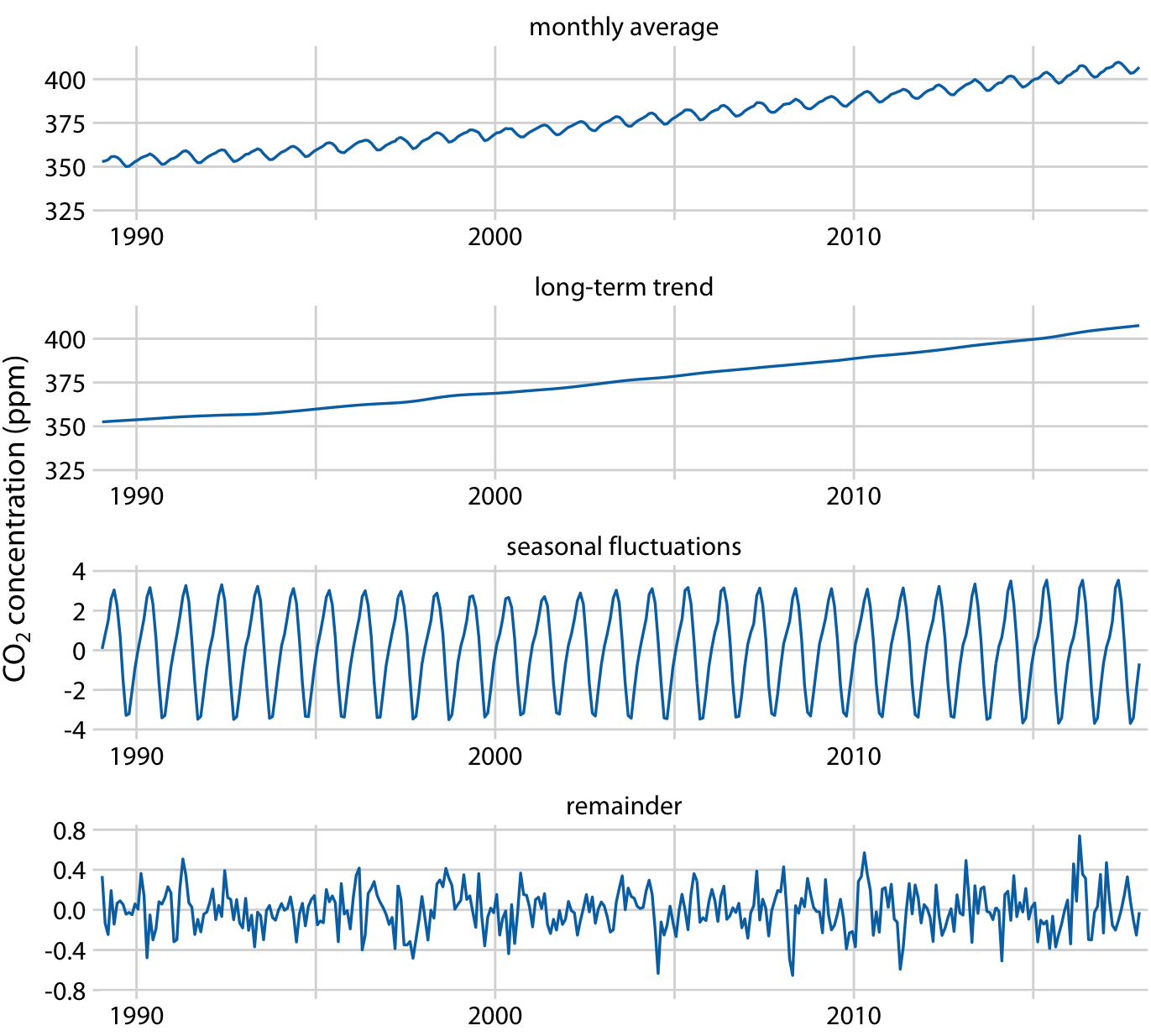
분해된 결과는 지난 30년 동안 CO2 농도가 50ppm 이상 증가했음을 보여줍니다. 이에 비해, 계절 변동은 8ppm 미만으로, 장기적인 추세에 비해 4ppm 이상의 증가나 감소를 일으키지 않습니다.나머지 구성 요소는 1.6ppm 미만이며, 이는 월별 CO2 농도 측정에서의 랜덤 노이즈에 해당합니다.