문제링크
https://school.programmers.co.kr/learn/courses/30/lessons/42895
문제설명
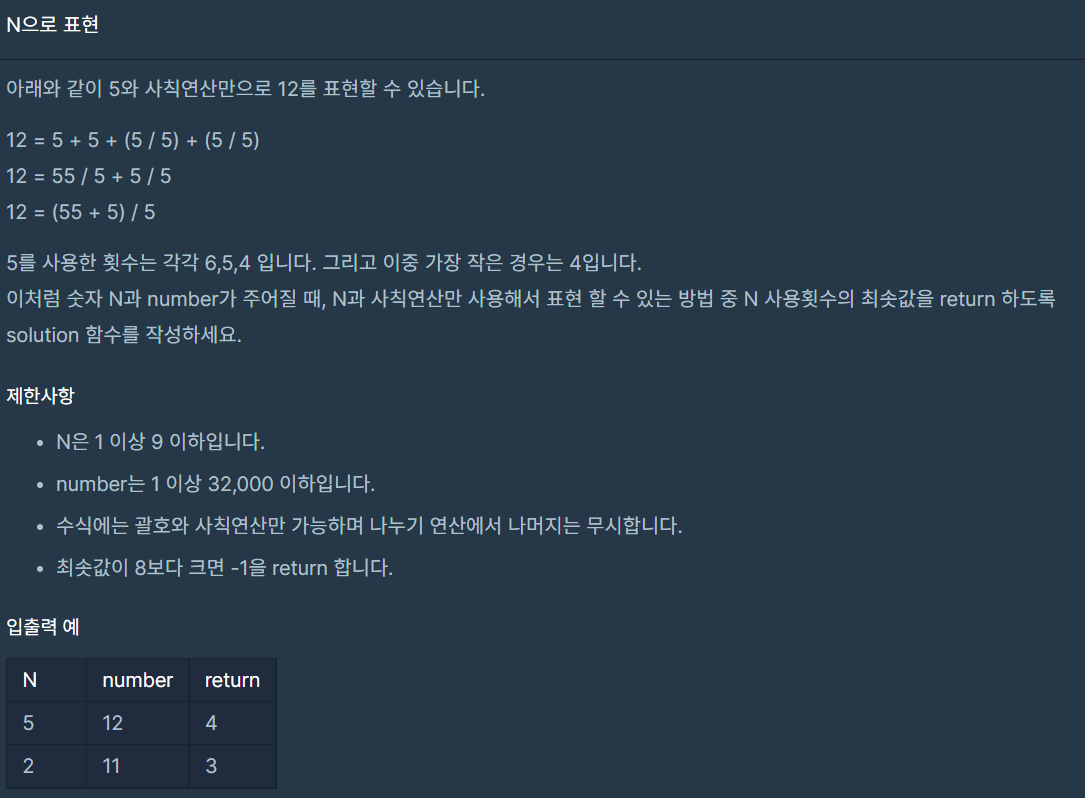
알고리즘

5를 5번 사용해서 만들 수 있는 숫자
- 55555
- 5를 1번 사용해서 만들 수 있는 숫자들 (+ - * /) 5를 4번 사용해서 만들 수 있는 숫자들
- 5를 2번 사용해서 만들 수 있는 숫자들 (+ - * /) 5를 3번 사용해서 만들 수 있는 숫자들
- 5를 3번 사용해서 만들 수 있는 숫자들 (+ - * /) 5를 2번 사용해서 만들 수 있는 숫자들
- 5를 4번 사용해서 만들 수 있는 숫자들 (+ - * /) 5를 1번 사용해서 만들 수 있는 숫자들
--> 일반화
숫자x를 n번 사용해서 만들 수 있는 숫자
- xx...x (x가 n개)
- x를 1번 사용해서 만들 수 있는 숫자들 (+ - * /) x를 (n-1)번 사용해서 만들 수 있는 숫자들
- x를 2번 사용해서 만들 수 있는 숫자들 (+ - * /) x를 (n-2)번 사용해서 만들 수 있는 숫자들
- x를 3번 사용해서 만들 수 있는 숫자들 (+ - * /) x를 (n-3)번 사용해서 만들 수 있는 숫자들
... - x를 n-1번 사용해서 만들 수 있는 숫자들 (+ - * /) x를 1번 사용해서 만들 수 있는 숫자들
코드
def solution(N, number):
# s[i] : 주어진 수 N을 i+1번 사용해서 만들 수 있는 수들의 집합
s = [set() for x in range(8)] # set 8개 초기화, 왜 8개를 만드냐? N 사용횟수가 8보다 크면 -1을 return하므로 N을 1개부터 8개 까지 사용하여 만든 값들이 number가 안될 경우 -1을 return한다.
for i, x in enumerate(s, start = 1): # 보통 첫번째 원소의 idx는 0인데 여기서는 첫번째 원소의 idx를 1로 시작한다.
x.add(int(str(N) * i)) # 8개의 set 각각 초기화, s[0] = N, s[1] = NN ... s[7] = NNNNNNNN (8개)
# s[i] 즉 N을 i+1개 사용했을 때 만들 수 있는 숫자 구하기.
for i in range(len(s)):
for j in range(i):
for op1 in s[j]: # op1 : 피연산자1, N을 j+1번 사용하여 만들 수 있는 숫자들
for op2 in s[i-j-1]: # op2 : 피연산자2, N을 i-j번 사용하여 만들 수 있는 숫자들
# op1과 op2를 사칙연산 --> 즉 N을 i+1번 사용하여 만들 수 있는 숫자를 구하게 되고 이를 s[i]에 대입
s[i].add(op1 + op2)
s[i].add(op1 - op2)
s[i].add(op1 * op2)
if op2 != 0:
s[i].add(op1 // op2)
if number in s[i]: # N을 i+1번 사용했을 때 찾고자하는 값 number가 존재한다면 i+1 return
answer = i + 1
break
else: # N을 8번 사용했는데도 찾고자하는 값 number가 존재하지 않는다면 -1 return
answer = -1
return answerex) N = 5라고 가정하자.
7번째 줄에서 i = 3 즉 s[3]을 구하려고 할 때 (이는 5를 4번 사용하여 만들 수 있는 숫자를 구하는 것과 같음)
5를 4번 사용해서 만들 수 있는 숫자
- 5555 (3번째 줄에서 초기화해줬음)
- 5를 1번 사용해서 만들 수 있는 숫자들 (+ - * /) 5를 3번 사용해서 만들 수 있는 숫자들
(1) j = 0일때
op1 = s[0] = 5를 1번 사용할 때 만들 수 있는 숫자들
op2 = s[2] = 5를 3번 사용해서 만들 수 있는 숫자들 - 5를 2번 사용해서 만들 수 있는 숫자들 (+ - * /) 5를 2번 사용해서 만들 수 있는 숫자들
(2) j = 1일때
op1 = s[1] = 5를 2번 사용할 때 만들 수 있는 숫자들
op2 = s[1] = 5를 2번 사용해서 만들 수 있는 숫자들 - 5를 3번 사용해서 만들 수 있는 숫자들 (+ - * /) 5를 1번 사용해서 만들 수 있는 숫자들
(3) j = 2일때
op1 = s[2] = 5를 3번 사용할 때 만들 수 있는 숫자들
op2 = s[0] = 5를 1번 사용해서 만들 수 있는 숫자들
