문제링크
https://school.programmers.co.kr/learn/courses/30/lessons/42860
문제설명

알고리즘
level2 치고 너무 어려웠던 문제였고 못풀었다. (나는 오른쪽 방향으로만 커서를 이동하는 방법, 왼쪽 방향으로만 커서를 이동하는 방법 이 두 가지만 고려해서 풀었기 때문에 틀림..)
결국 다른 사람 코드 보면서 이 문제를 풀려고 했으나 이해하는데 너무 오래걸렸다.ㅜㅜ 다른사람코드는 다음과 같다.
def solution(name):
answer = 0
n = len(name)
def alphabet_to_num(char):
num_char = [i for i in range(14)] + [j for j in range(12, 0, -1)]
return num_char[ord(char) - ord('A')]
for ch in name:
answer += alphabet_to_num(ch)
move = n - 1
for idx in range(n):
next_idx = idx + 1
while (next_idx < n) and (name[next_idx] == 'A'):
next_idx += 1
distance = min(idx, n - next_idx)
move = min(move, idx + n - next_idx + distance)
answer += move
return answer이제 위 코드를 자세히 살펴보자.
위 코드는 상, 하 조작 횟수와 좌, 우 조작 횟수를 따로 구한 후 더해주었다.
상, 하 조작 횟수
상, 하 조작 횟수는 아래 코드로 구할 수 있다.
def alphabet_to_num(char):
num_char = [i for i in range(14)] + [j for j in range(12, 0, -1)]
return num_char[ord(char) - ord('A')]
for ch in name:
answer += alphabet_to_num(ch)좌, 우 조작 횟수 (즉 커서 이동 횟수)
두번째 for문은 커서 이동 수를 구하는 코드이다.
커서를 이동시키는 방법은 다음과 같이 크게 3가지 존재한다.
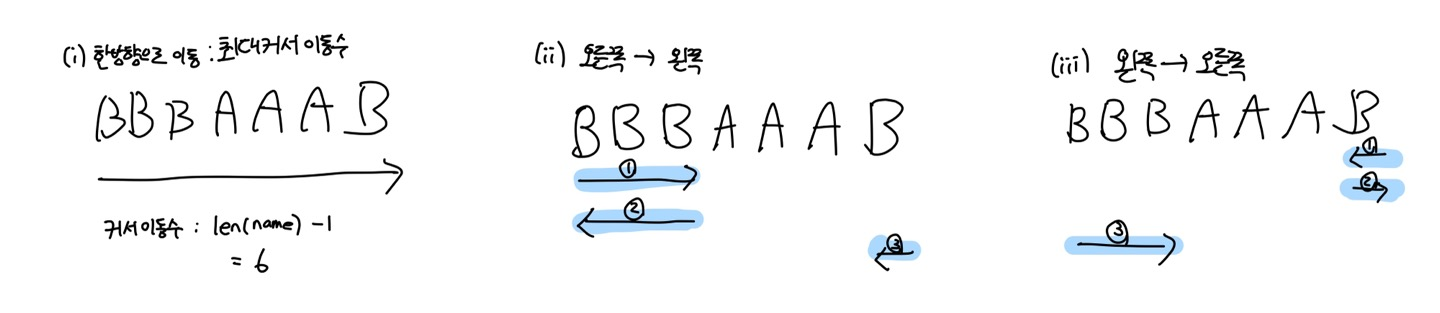
위 그림에서 알 수 있듯이 두번째 방법과 세번째 방법을 구하려면 알파벳 "A"의 위치를 알아야 한다. 그것을 구하는 코드가 바로 아래와 같다.
for idx in range(n):
next_idx = idx + 1
while (next_idx < n) and (name[next_idx] == 'A'):
next_idx += 1여기서 구한 idx가 알파벳 "A"의 직전 index가 되고, next_idx는 다음 "A"가 나온 직후의 index가 된다.
위 예시(BBBAAAB)에서 "A"의 index는 3이고 그 다음 "A"의 index는 5이므로
idx는 2, next_idx는 6이된다.
또다른 예시 : BBBAABAAAB
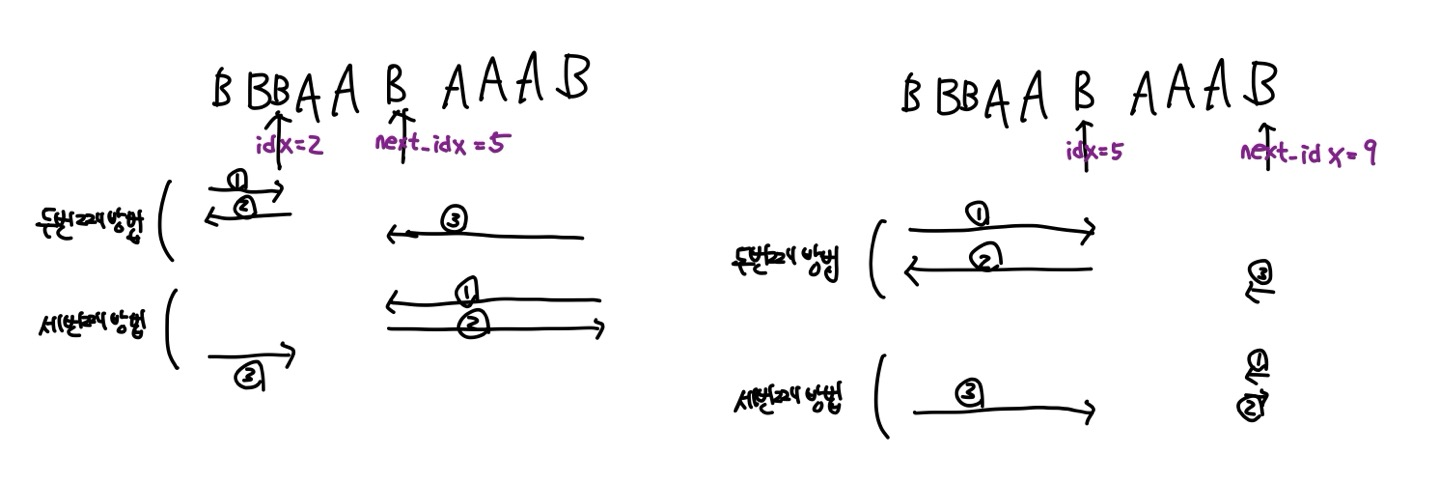
위 예시에서는 idx = 2, next_idx = 5인 경우 뿐만 아니라
idx = 5, next_idx = 9인 경우도 고려해야한다.
커서를 이동시키는 3가지 방법을 좀 더 구체적으로 살펴보자.
-
한 방향(오른쪽)으로만 이동. 이는 즉 최대 커서 이동수가 된다.
len(name)-1 만큼 움직이게 된다. -
오른쪽 -> 왼쪽
- 0에서 시작
- -> "A"가 나오기 직전의 index(idx)까지 오른쪽으로 이동 (idx만큼 이동)
- -> 다시 왼쪽으로 이동하며 0으로 돌아옴 (idx만큼 이동)
- -> 다음 "A"가 나오기 직후의 index(next_idx)까지 왼쪽으로 이동 (n-next_idx 만큼 이동)
- 왼쪽 -> 오른쪽
- 0에서 시작
- -> 다음 "A"가 나오기 직후의 index(next_idx)까지 왼쪽으로 이동 (n-next_idx 만큼 이동)
- -> 다시 오른쪽으로 이동하며 0으로 돌아옴 (n-next_idx 만큼 이동)
- -> "A"가 나오기 직전의 index(idx)까지 오른쪽으로 이동 (idx만큼 이동)
최소 커서 이동 횟수를 구하려면 2번의 idx와 3번의 n-next_idx를 비교해야한다. 그리고 이 값을 distance 변수에 담게 된다.
distance = min(idx, n - next_idx)
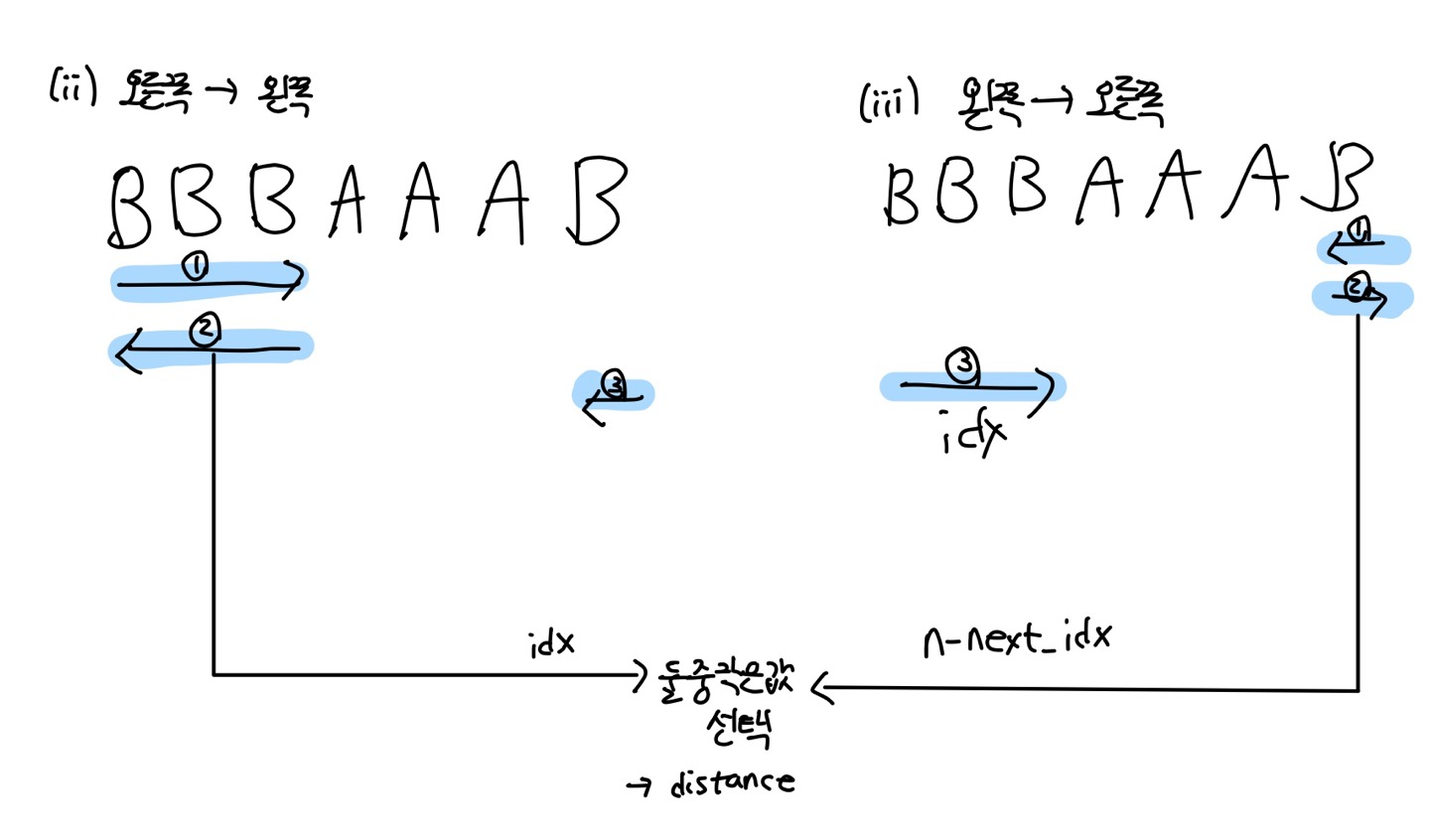
위 예시에서는 idx(2)와 n-next_idx(7-6=1) 중 n - next_idx가 더 작으므로 distance는 1이 되고 우리는 세번째 방법으로 커서를 이동하게 된다.
distance를 구하게 되면 이제 최소 커서 이동 횟수를 구할 수 있다.
세번째 방법을 사용하여 커서 이동 횟수를 구하면.. (idx와 n - next_idx 중 n - next_idx 중 n - next_idx가 더 작은 경우, 즉 distance = n - next_idx)
먼저 distance 만큼 왼쪽으로 이동하게 되고(distance)
-> distance 만큼 오른쪽으로 이동한다. (distance)
-> idx만큼 이동한다.
-> distance + distance + idx 가 커서 이동 횟수가 된다.
하지만 만일 두번째 방법으로 커서를 이동하게 된다면 ( idx와 n - next_idx 중 idx가 더 작은 경우, 즉 distance = idx)
먼저 distance 만큼 오른쪽으로 이동하게 되고 (distance)
-> distance만큼 왼쪽으로 이동한다. (distance)
-> n - next_idx 만큼 왼쪽으로 이동한다. (n - next_idx)
-> distance + distance + n - next_idx
따라서 위 두 경우를 모두 고려한 커서 이동 횟수 식은 다음과 같다.
distance + idx + (n - next_idx)
그리고 이 값과 이전에 구한 최소 커서 이동 수(move)와 비교하여 둘 중 작은 값으로 커서를 이동하게 된다.
move = min(move, idx + n - next_idx + distance)
그 후 for문으로 모든 index를 거친 후 마지막에 나온 move값이 최소 커서 이동 횟수가 된다.
다른 사람 코드 보면서 내가 이해한 내용은 위와 같은데.. 맞게 이해한건지는 잘 모르겠다.. 근데 대충 이런 알고리즘으로 문제를 해결했다고 생각하면 될 것 같다..😂😂
