[Paper Review] - W-MSE(Whitening Mean Squared Error, 2021, ICML)

[Main Contribution]

• Whitening MSE(W-MSE)라는 새로운 Self supervised learning loss function을 제안.
  • 배치 샘플을 구형 분포(spherical distribution)에 놓이도록 제약하며, 기존 positive-negative instance contrastive learning기반 방법론 대체 가능
• negatives 샘플들을 필요로 하지 않기 때문에, 배치 내에서 더 많은 positive 샘플을 포함할 수 있다.
  • (실험적으로 하나의 이미지에서 다수의 양성 샘플을 추출하는 것이 성능을 향상시킴을 입증)
• 기존 contrastive loss 방법론보다 뛰어난 성능을 보이며, 최신 self supervised learning 방법들과 비교했을때 경쟁력이 있다. (vs BYOL(2020), SimSiam(2020))

cf) collapse(개념 숙지!!)

• argumentation에서 뽑은 두 embedding vector 사이의 MSE가 줄어들도록 학습을하면 ex) [1,1,1], [1,1,1] 이런식으로 되면 encoder 가 의미있는 정보를 못뽑음.
  • Encoder(인코더)가 의미 있는 특징 벡터를 추출해야 하는데, Collapse가 발생하면 제대로 추출하지 못함.
  • 우리는 그 Encoder를 학습시켜서 각각의 입력 데이터에 대해 의미 있는 표현(embedding)을 생성하도록 만듦.
  • 하지만 Collapse가 발생하면 → Encoder가 모든 입력 데이터에 대해 거의 동일한 벡터를 반환하게 됨 → 모델이 구별할 수 있는 정보가 사라짐.

[The Whitening MSE Loss]

문제점

contrasive learning 문제점

• negative sample을 확보하는것이 어려움.

non contrastive learning(distiliation method)

• positive pair만을 가지고 학습할 경우 생기는 collapse를 방지하기 위해 asymmetric architecture, stop gradient(distiliation 방법론)등의 구조적 제약이 존재

[overview]

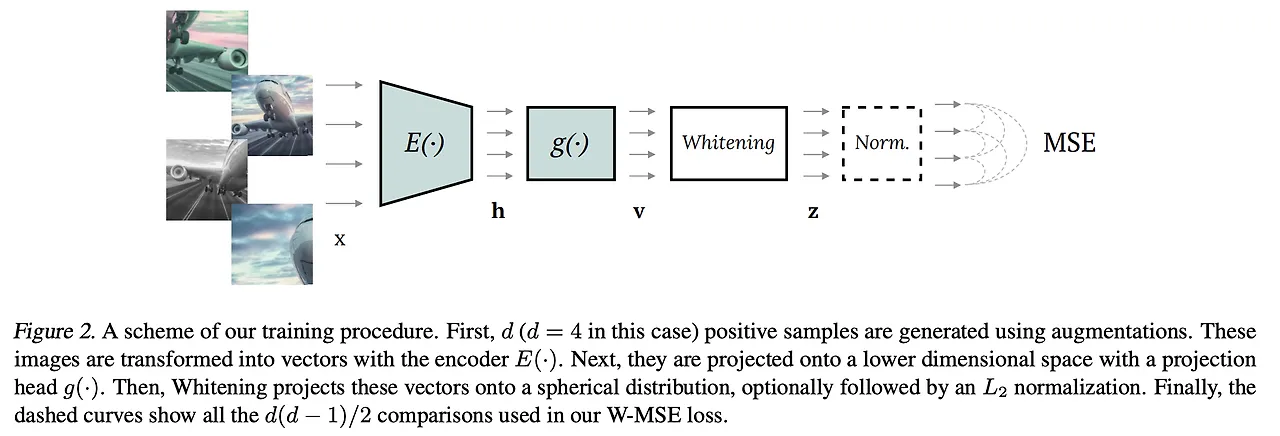
notation

• x : image
• d : 데이터 증강 횟수
• E(⋅) : ResNet
• h : average pooling
• g(⋅) : BN(Batch Normalization) 레이어가 포함된 1개의 은닉층을 가진 MLP
• z : whitening transform 적용한 임베딩 벡터

[objective function & constraints]

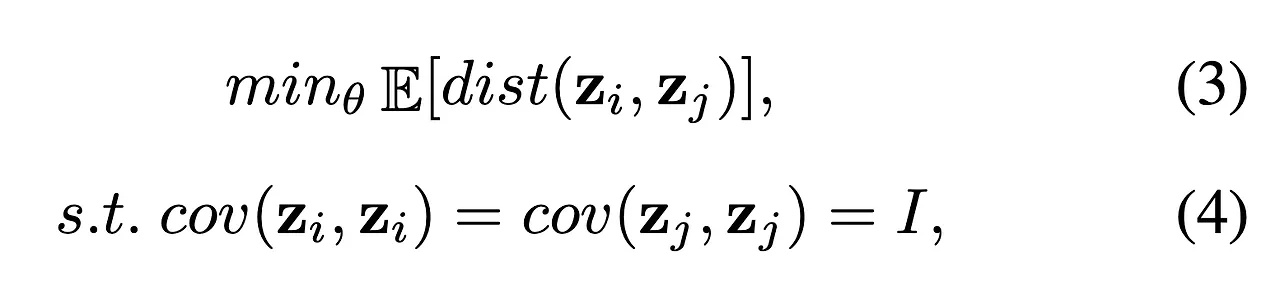
• positive pairs 사이의 거리 를 최소화
• 임베딩 벡터 z의 공분산 행렬이 단위 행렬이 되도록

→ 이를 통해 collapse 방지.

1. [Whitening transformation]

$\mu_V = \frac{1}{K} \sum_k v_k$

$\Sigma_V = \frac{1}{K - 1} \sum_k (v_k - \mu_V)(v_k - \mu_V)^T$

$W_V^T W_V = \Sigma_V^{-1}$

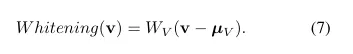
• 모든 embedding vector를 평균이 0이고, 공분산 행렬이 단위 행렬인 분포로 변환하는 선형변환
• Whitening transformation을 통해 임베딩 벡터 V를 Z벡터로 선형변환

💡 Whitening 변환을 통해 **Spherical distribution**을 따르도록 조정

• 표현 붕괴(Collapse)를 방지하고,
• 모델이 균일한 표현을 학습할 수 있도록 도움.

[Loss function]

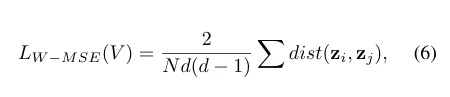
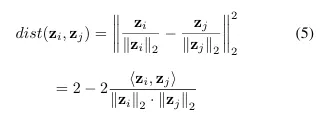
2. [Batch slicing]

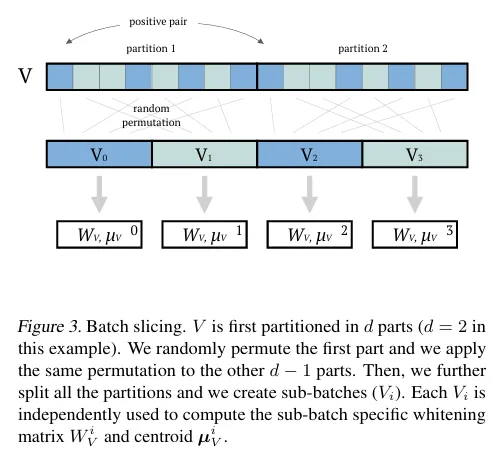
• 모든 데이터에 한번에 whitening transform을 적용하는것이 아님
• 배치에 따라 구해지는 $\mu_V$, $W_V$가 다르기 때문에 안정성을 위해 batch slicing 기법을 제안
• d : 한 이미지에서 생성된 양성 샘플수(데이터 증강 횟수)

💡Batch Slicing 과정

1. V를 d개의 부분으로 나눈다. (이 예에서는 d=2)
2. 첫 번째 부분을 무작위로 랜덤하게 섞고(random permutation),동일한 섞기 순서를 다른 d−1개의 부분에도 적용한다.
3. 그런 다음, 각 부분을 다시 서브 배치(V)별로 나누고 $μ_V$, $W_V$ 를 계산하여 whitening을 적용

[학습의 불안정성?]

• 배치 크키가 작을경우 공분산 행렬이 불안정해져서 학습이 불안정 할 수 있지만

→ 이 과정을 같은 배치내에서 여러 번 반복하여 평균을 냄

→ Whitening 행렬이 특정 샘플에 과하게 의존하지 않도록 학습 가능.

💡 최종 손실(loss) 계산 시, 모든 Whitening 결과를 결합하여 사용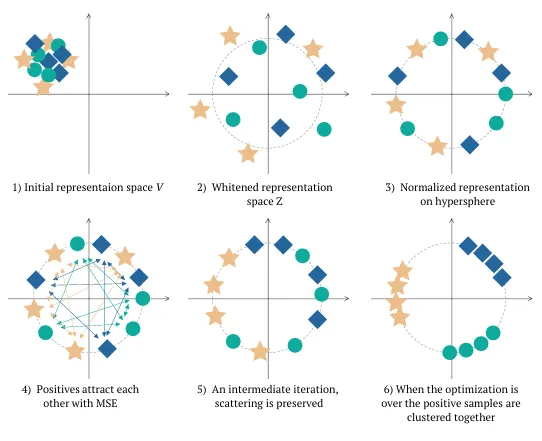

실험

• 데이 증강 횟수(d)가 2일때, 4일때에 대해 실험진행.
• SimCLR(constrastive learning), BYOL(distiliation)

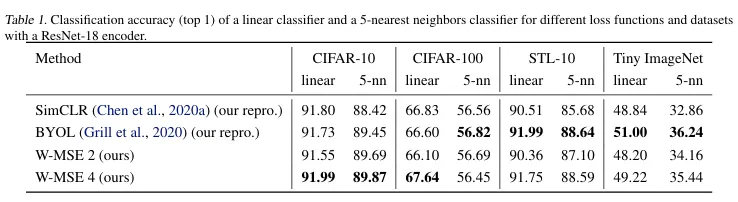
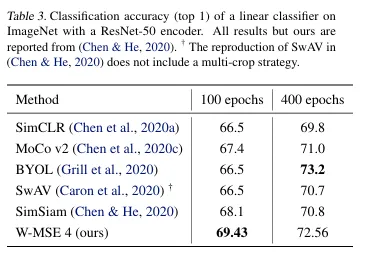
Conclusion

• Self-Supervised Learning(SSL)에서 사용되는 손실함수들과 다른 차별화된 새로운 손실함수인 W-MSE 제안.
• BYOL, SimSiam(오직 양성 샘플 사용) : 비대칭 학습(asymmetry in learning) 특정 학습 프로토콜 적용
• 본인들의 W-MSE가 훨씬 단순한 방식 사용하면서도 기존의 SOTA 방법들과 동등하거나 더 나은 분류 정확도를 낸다.
• 비대칭 학습(asymmetry in learning)과 Whitening 변환(whitening transformation)은서로 대체 가능한 해결책이지만, 이를 결합하는 것도 가능하며, 이는 향후 연구의 방향이 될 수 있다