가치 기반 학습(Value-Based Learning)과 정책 기반 학습(Policy-Based Learning)

• 강화학습의 핵심 목표: 환경과의 상호작용을 통해 기대되는 누적 보상(expected cumulative reward)을 최대화하는 정책(Policy)을 학습하는 것.
• 이는 에이전트가 어떤 상태에서 어떤 행동을 선택해야 할지를 학습하여 장기적으로 최적의 결과를 얻는 것을 의미합니다.

강화학습은 크게 가치 기반 학습과 정책 기반 학습으로 나뉩니다.

1. 가치 기반 학습 (Value-Based Learning)

• 상태(state, state-action)의 가치 함수를 학습하고 이를 바탕으로 행동을 선택.
• 대표적인 알고리즘: Q-Learning, SARSA.
• Q-값(Q-Value): 특정 상태 $s$에서 행동 $a$를 취했을 때 기대되는 총 보상 $Q(s, a)$를 학습합니다.
• 최적 정책은 다음과 같이 정의됩니다: $\pi^*$(s) = $argmax_a Q(s, a)$

2. 정책 기반 학습 (Policy-Based Learning)

• 정책 함수 $\pi^*(a|s)$를 직접 학습합니다.
• 대표적인 알고리즘: Actor-Critic.
• 연속적인 행동 공간에서도 적용 가능하며, 직접 정책을 최적화합니다.

3. 가치 함수(Value Function)와 정책 함수(Policy Function)

• 가치 함수(Value Function): 상태나 상태-행동 쌍의 "가치"를 나타냅니다.
  • 상태 가치 함수 $V(s)$: 특정 상태 $(s$)의 가치. 지금부터 기대되는 return
  • 행동 가치 함수 $Q(s, a)$: 특정 상태 $(s$)에서 행동 $(a$)를 취했을 때의 가치. 지금 행동으로부터 기대되는 Return
• 정책 함수(Policy Function): 상태 $(s$)에서 행동 $(a$)를 선택할 확률을 나타냅니다.

4. 탐험과 활용 문제 (Exploration vs Exploitation)

• 탐험(Exploration): 새로운 정보를 탐색하기 위해 무작위 행동을 선택.
• 활용(Exploitation): 현재 학습된 최적 행동을 선택하여 보상을 극대화.
• 균형 유지가 중요하며, $epsilon$-탐욕적 정책($epsilon$-greedy)을 사용해 해결합니다.
• $epsilon$-탐욕적 정책: 초기에는 탐험을 많이하고 점차 줄여나가는 정책

정책 이터레이션

• 정책 이터레이션(Policy Iteration)은 가치 기반 학습(Value-Based Learning)에 속함

• 정책 이터레이션은 주어진 정책 하에서 벨만 기대 방정식을 사용해 가치를 평가하고 개선

• 정책 이터레이션은 초기 정책으로 시작해서 점진적으로 개선하여 최적 정책에 도달하는 알고리즘

• 정책 이터레이션은 정책 평가와 정책 개선 단계를 번갈아 수행하면서 최적의 정책을 찾음

• 정책 평가(Policy Evaluation):

  • 현재 정책 하에 각 상태의 가치를 계산. 이 과정에서, 벨만 기대 방정식을 사용하여 모든 상태에 대해 가치 함수를 반복적으로 계산하며, 이는 현재 정책을 따랐을 때 각 상태에서 기대할 수 있는 장기적인 보상의 총합을 의미함

• 정책 개선(Policy Improvement):

  • 계산된 가치 함수 $V^\pi(s)$)를 바탕으로 정책을 업데이트.
    정책이 더 이상 개선되지 않을 때(수렴할 때)까지 두 단계를 반복
    상태 가치 함수를 사용하여 최적의 정책을 도출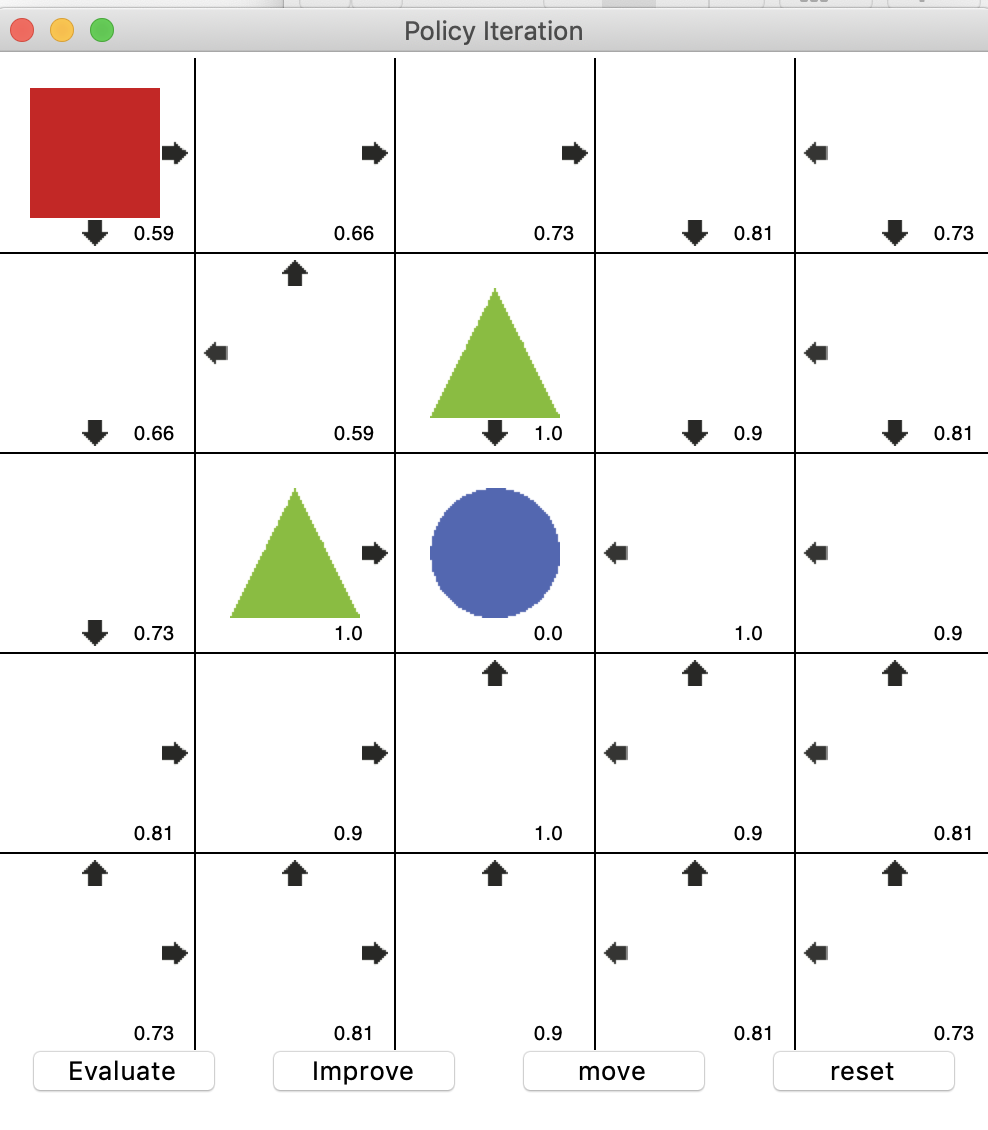

    

• Rule : 세모(-1)를 피해 동그라미(1)에 최단 경로로 도달하여 보상을 획득하는 것이 목적임
• 정책 평가(Evaluate) : 현재 정책에 따라 각 상태의 가치를 계산. 즉, 상태에서 가능한 모든 행동에 대한 기대 보상을 계산하고, 그 값을 바탕으로 상태의 가치를 업데이트
• 정책 개선(Improve) : 각 상태에서 가능한 행동 중, 가장 큰 보상(즉, 더 높은 상태 가치를 제공하는 행동)을 취할 확률이 더 높도록 정책 개선
  Move : 현재까지의 정책을 기반으로 에이전트 이동 시작

알고리즘

1. 초기화:
   • 초기 정책 $(\pi_0$)를 무작위로 설정.
2. 반복:

   • 정책 평가: 현재 정책 $\pi_k$에 대한 가치 함수 $(V^{\pi_k}(s)$) 계산.

     $^\pi(s) = \sum_{a} \pi(a|s) \sum_{s'} P(s'|s, a) \big[ R(s, a, s') + \gamma V^\pi(s') \big]$

• 정책 개선: 가치 함수 $(V^{\pi_k}(s)$)를 사용해 새로운 정책 $(\pi_{k+1}$) 도출.

  $\pi_{k+1}(s) = \arg\max_a \sum_{s'} P(s'|s, a) \big[ R(s, a, s') + \gamma V^{\pi_k}(s') \big]$

3. 정책이 수렴할 때 종료.

특징

• 장점: 정책과 가치 함수를 동시에 업데이트하기 때문에 수렴 속도가 빠름.
• 단점: 정책 평가 단계가 반복적으로 수행되므로 계산 비용이 클 수 있음.

가치 이터레이션

• 가치 이터레이션(Value Iteration)은 가치 기반 학습(Value-Based Learning)에 속함

• 가치 이터레이션은 각 반복에서 직접적으로 최적의 가치 함수를 추정하고, 이를 바탕으로 최적의 정책을 결정함.

• 이 방법은 정책 평가와 정책 개선 단계를 하나로 합쳐 더 효율적으로 계산할 수 있게 해줌.

• 가치 함수 업데이트:

  • 모든 상태에 대해 가능한 모든 행동의 결과를 고려하여, 각 상태의 가치 함수를 업데이트함
  • 벨만 최적 방정식을 사용하여, 각 상태에서 가능한 행동 중에서 최대의 기대 가치를 제공하는 행동을 통해 가치 함수를 업데이트함.
  • 이렇게 계산된 가치 함수를 기반으로, 각 상태에서 가능한 행동들 중에서 가장 - 높은 가치를 제공하는 행동을 선택하여 최적의 정책을 결정함.

• 가치 이터레이션은 일반적으로 정책 이터레이션보다 더 빠르게 수렴할 수 있으며, 계산 과정이 좀 더 단순함

  

알고리즘

1. 초기화:

   • $V(s)$를 임의의 값으로 초기화 (예: $V(s) = 0$).

2. 반복:

   • 벨만 최적 방정식을 사용해 (V(s))를 업데이트:

     $V(s) \leftarrow \max_a \sum_{s'} P(s'|s, a) \big[ R(s, a, s') + \gamma V(s') \big]$

   • $V(s)$가 수렴할 때까지 반복.

3. 최적 가치 함수 $V^*(s)$를 바탕으로 최적 정책 계산:

특징

• 장점: 정책 평가와 정책 개선 단계를 한 번에 수행하므로 계산이 간단하고 직관적.
• 단점: 더 많은 반복이 필요할 수 있음.

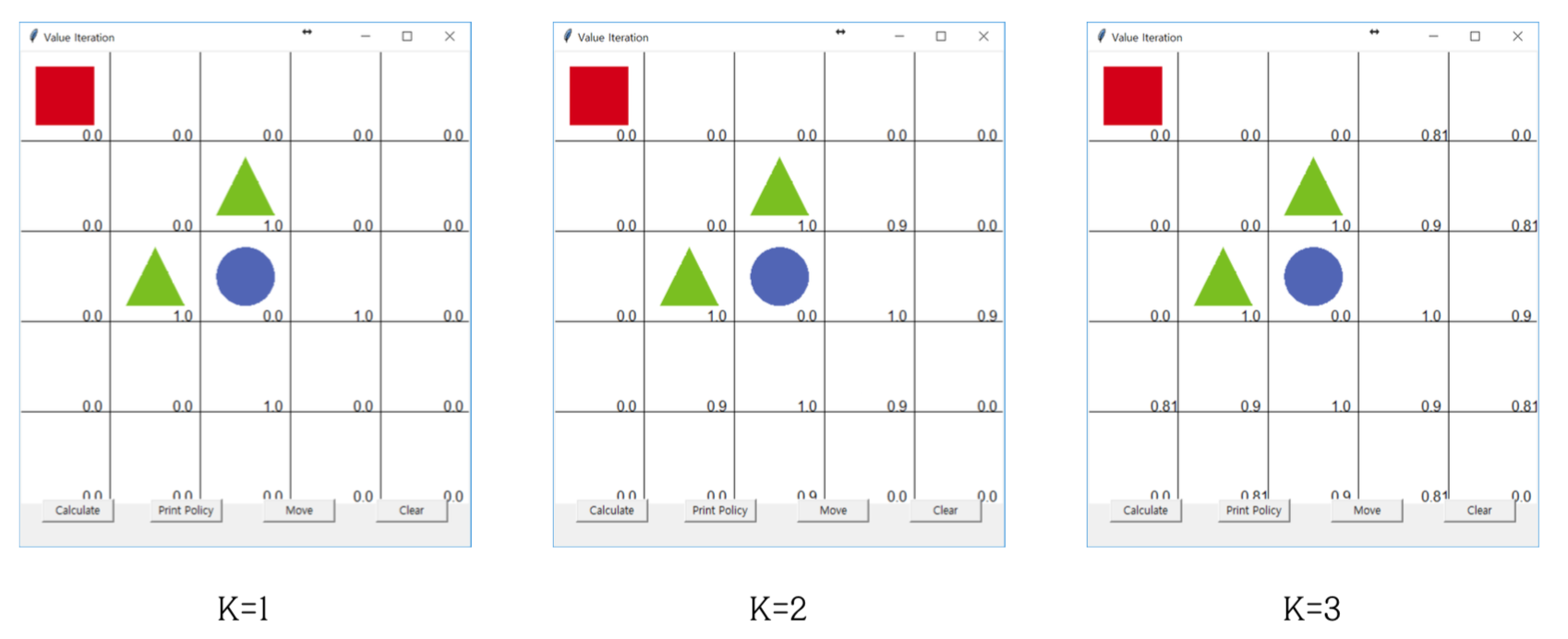
value_iteration.py 파일 실행

• Rule : 세모(-1)를 피해 동그라미(1)에 최단 경로로 도달하여 보상을 획득하는 것이 목적임
• 계산(Calculate) : 각 상태에 대해 최적의 행동을 결정하기 위한 가치를 계산하고 업데이트
• Print Policy : 현재 추정된 최적의 정책을 시각적으로 표시
• Move : 현재까지의 정책을 기반으로 에이전트 이동 시작
• Clear : 최초 실행 상태로 초기화

위 내용에 대한 실습 코드는 https://github.com/rlcode/reinforcement-learning-kr 에서 참조했습니다!