Memory Technology

SRAM (Static RAM)

• 0.5ns ~ 2.5ns
• $2000 ~ $5000 per GB

DRAM (Dynamic RAM)

• 50ns ~ 70ns
• $20 ~ $75 per GB

• capacitor(축전기)에 전하를 저장하기 때문에 무한히 저장될 수 없어서
  주기적으로 리프레시가 필요하다.
  (water tank with little hold
  -> you have to refill the tank periodically)

Magnetic disk

• 5ms ~ 20ms
• $0.2 ~ $2 per GB

Ideal Memory

• Access time of SRAM
• Capacity and cost/GB of disk

---

Principle of Locality

• program은 어떤 특정 시간에는 address space(주소 공간) 내의 비교적 작은 부분에만 접근한다는 원칙

Temporal locality (시간적 지역성)

• Items accessed recently are likey to be accessed again soon
• e.g.) instructions in a loop, induction variables (like i)

Spatial locality (공간적 지역성)

• Items near those accessed recently are likey to be accessed soon
• e.g.) sequential instruction access, array date

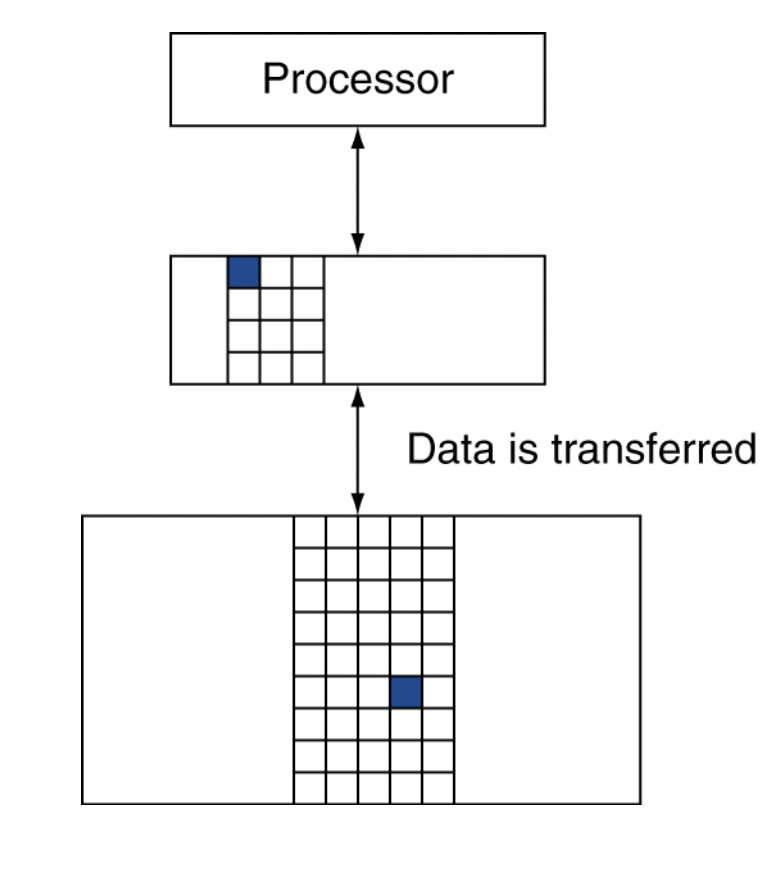
Taking Advantage of Locality

• Memory hierarchy (메모리 계층구조)
• Store everything on disk
• Copy recently accessed (and nearby) items
  from disk to smaller DRAM memory
  • Main memory
• Compy more recently accessed (and nearby) items
  from DRAM to smaller SRAM memory
  • Cache memory attaced to CPU

---

Memory Hierarchy Level

메모리 계층구조

• 서로 다른 속도와 크기를 갖는 여러 계층의 메모리로 구성되어 있다.
• 빠른 메모리는 느린 메모리보다 비트당 가격이 비싸기 때문에 주로 그 크기가 작다.
• 빠른 메모리는 프로세서에 가깝게 둔다

• 사용자에게 가장 빠른 메모리가 갖는 접근 속도를 제공하면서
  동시에 가장 싼 기술로 최대한 큰 메모리 용량을 제공한다

• block (or line) : 두 계층 간 정보의 최소 단위. (unit of copying)

• hit : 프로세서가 요구한 데이터가 상위 계층의 어떤 블록에 있을 때
• miss : 상위 계층에서 찾을 수 없을 때.
  • 필요한 데이터를 포함하는 블록을 찾기 위해 하위 계층 메모리에 접근

• hit time : 상위 계층에 접근하는 시간
  (접근이 hit인지 miss인지 결정하는데 필요한 시간이 포함)
• miss penalty
  : 하위 계층에서 해당 블록을 가져와서 상위 계층 블록과 교체하는 시간 +
  그 블록을 프로세서에 보내는 데 걸리는 시간

---

Cache Memory

• 메모리 계층 구조에서 CPU와 가까이 있는 level

• 데이터가 캐시 내에 있는지 어떻게 알 수 있을까?
• 알 수 있다면, 어떻게 찾을 수 있을까?

Direct Mapped Cache

• 메모리 주소가 위치를 결정한다
• 각 메모리 위치는 cache 내의 딱 한 장소에 mapping된다
  • (블록 주소) modulo (cache 내의 전체 cache 블록 수)
  • 블록 수가 power of 2 형식이면,
    modulo는 간단히 주소의 하위 log2(전체 블록 수)로 쉽게 계산할 수 있다.
    
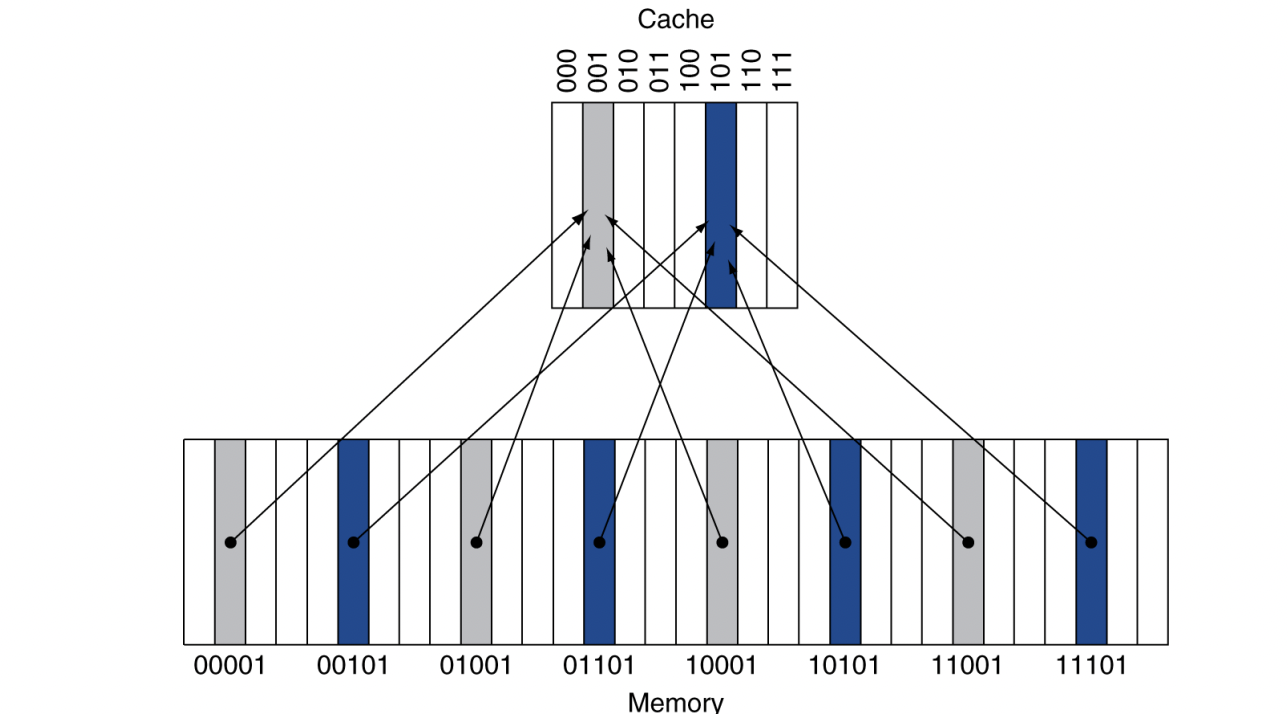
  • 위 그림에서 cache의 전체 블록 수는 8개 이므로,
    메모리 주소의 LSB 3 bits를 확인해서 cache 내의 위치를 결정할 수 있다.

• 그럼 이제 저 4개 중에 어떤게 mapping되었는지 알아야 한다
  • cache에 저장할 때 data뿐만 아니라 block address도 같이 저장한다
  • 이 때, 아래 3bit를 저장할 필요는 없고, 위 2 bits만 저장한다
  • 이를 Tag bit라고 한다

• 그럼 cache 블록이 유효한 정보를 가지고 있는지도 알아내야 한다.
  예를 들어, 맨 처음에는 cache가 다 비어 있을 것이고, 이 때의 tag bit는 의미가 없다.
  • Valid bit가 1이면 유효한 블록이 있고, 0이면 유효한 블록이 없는 것으로 간주한다
  • Initially 0

Example

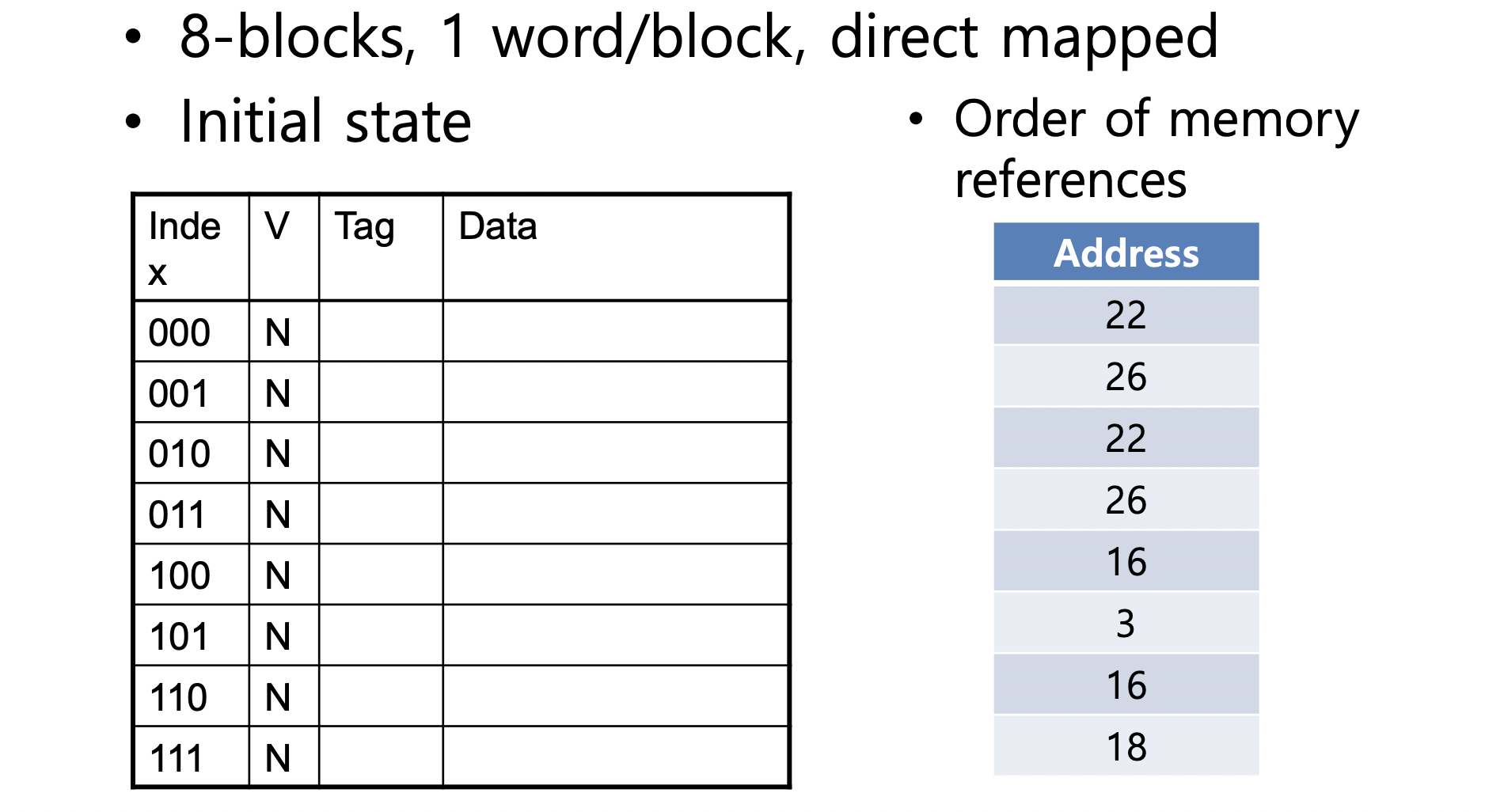
• Word addr	Binary addr	Hit/Miss	Cache block
  22	10 110	Miss	110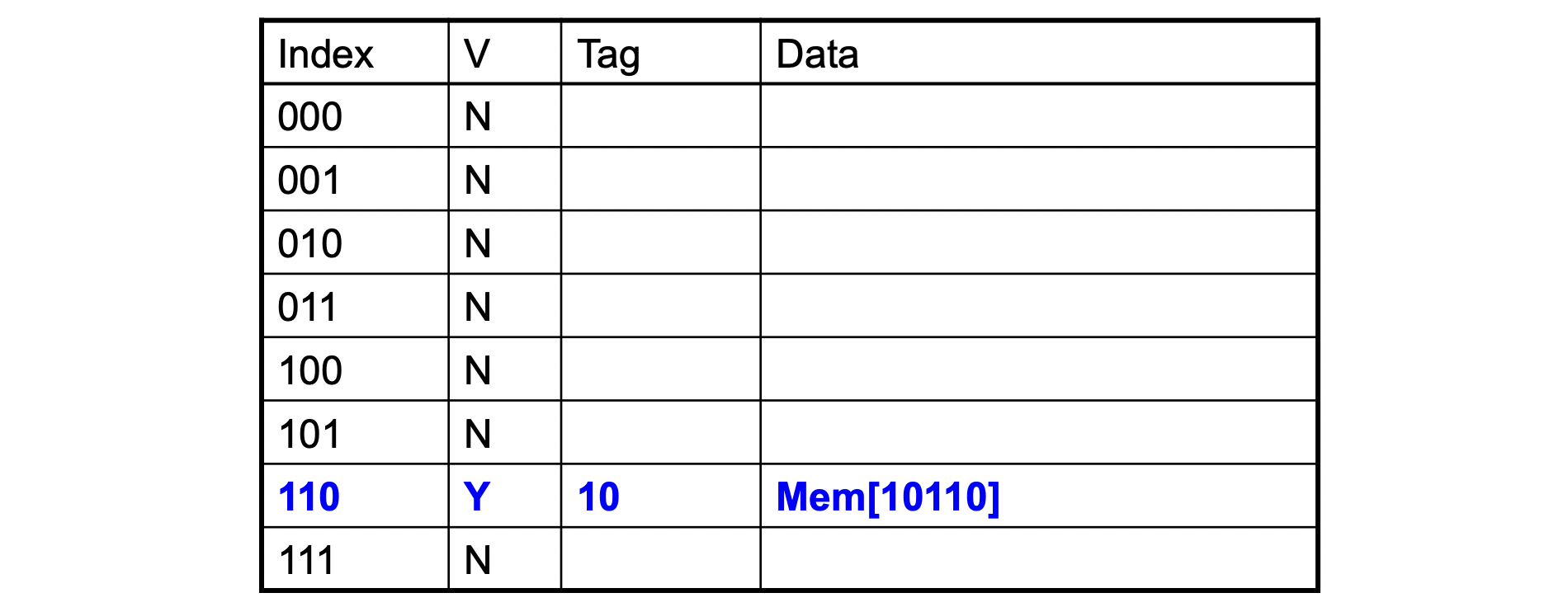

  

• Word addr	Binary addr	Hit/Miss	Cache block
  26	11 010	Miss	010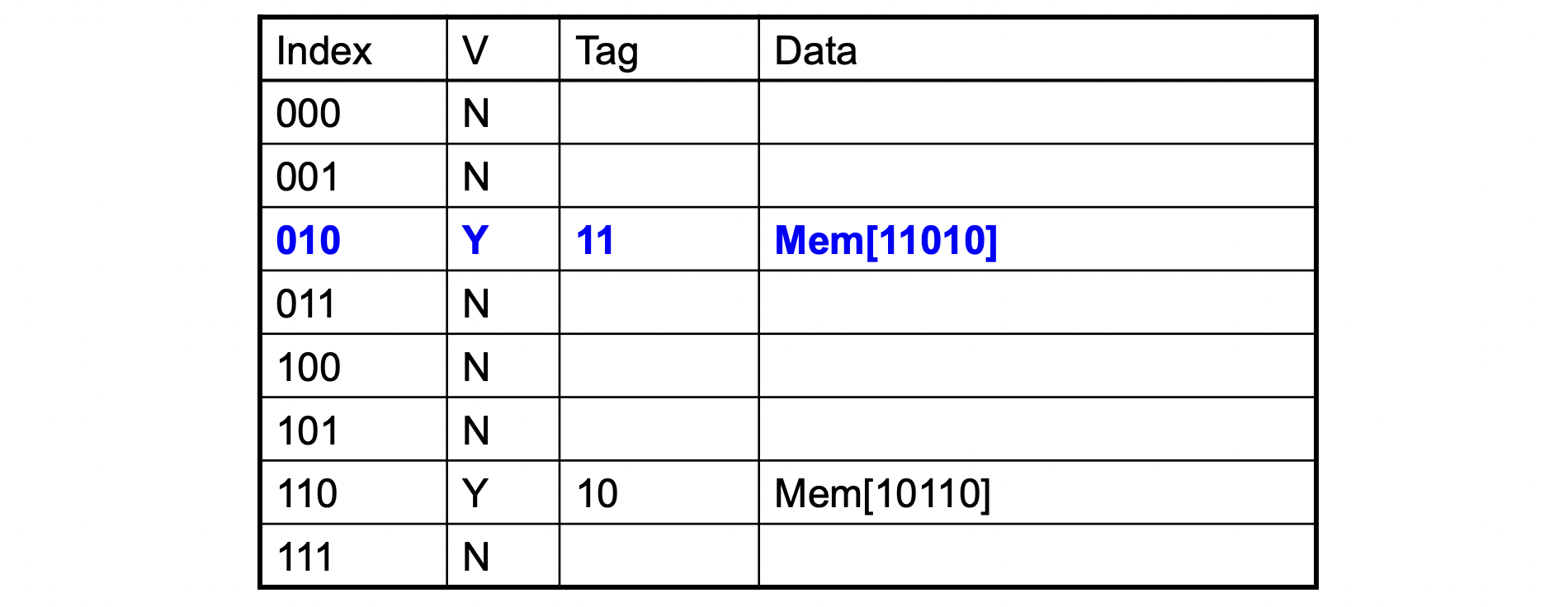

  

• Word addr	Binary addr	Hit/Miss	Cache block
  22	10 110	Hit	110
  26	11 010	Hit	010

• Word addr	Binary addr	Hit/Miss	Cache block
  16	10 000	Miss	000
  3	00 011	Miss	011
  16	10 000	Hit	000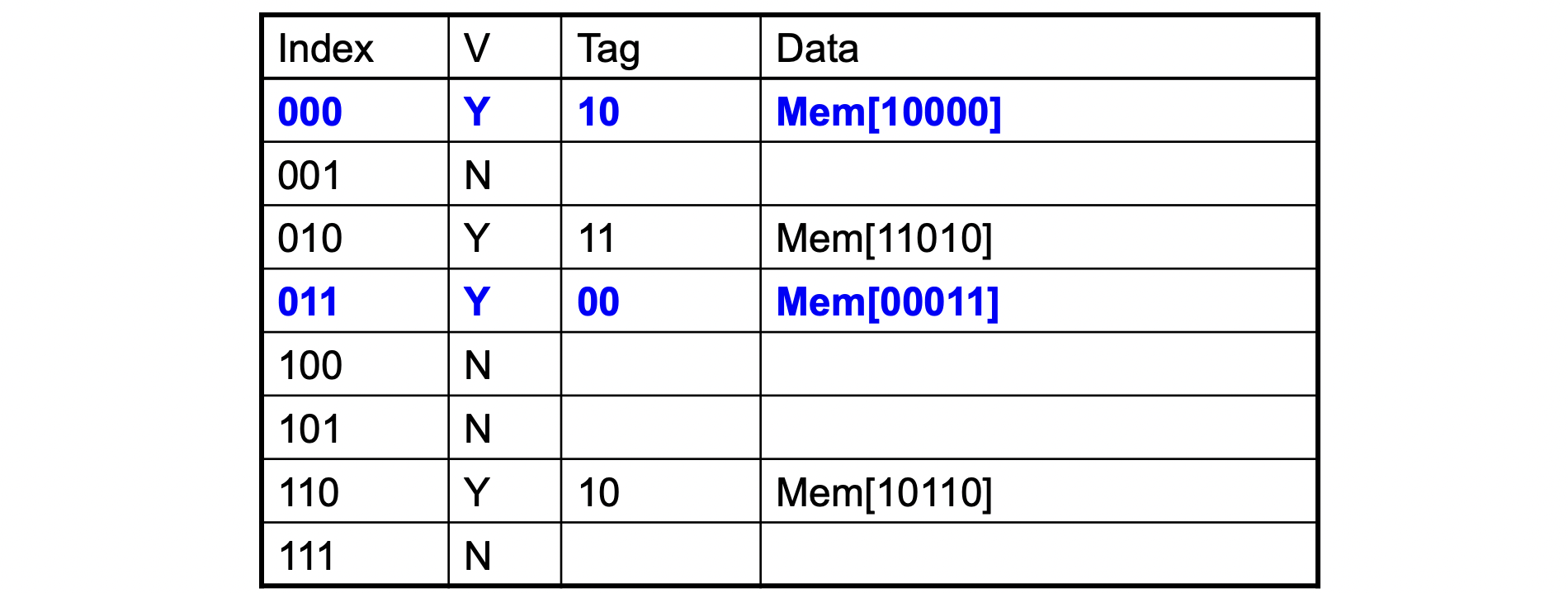

  

• Word addr	Binary addr	Hit/Miss	Cache block
  18	10 010	Miss	010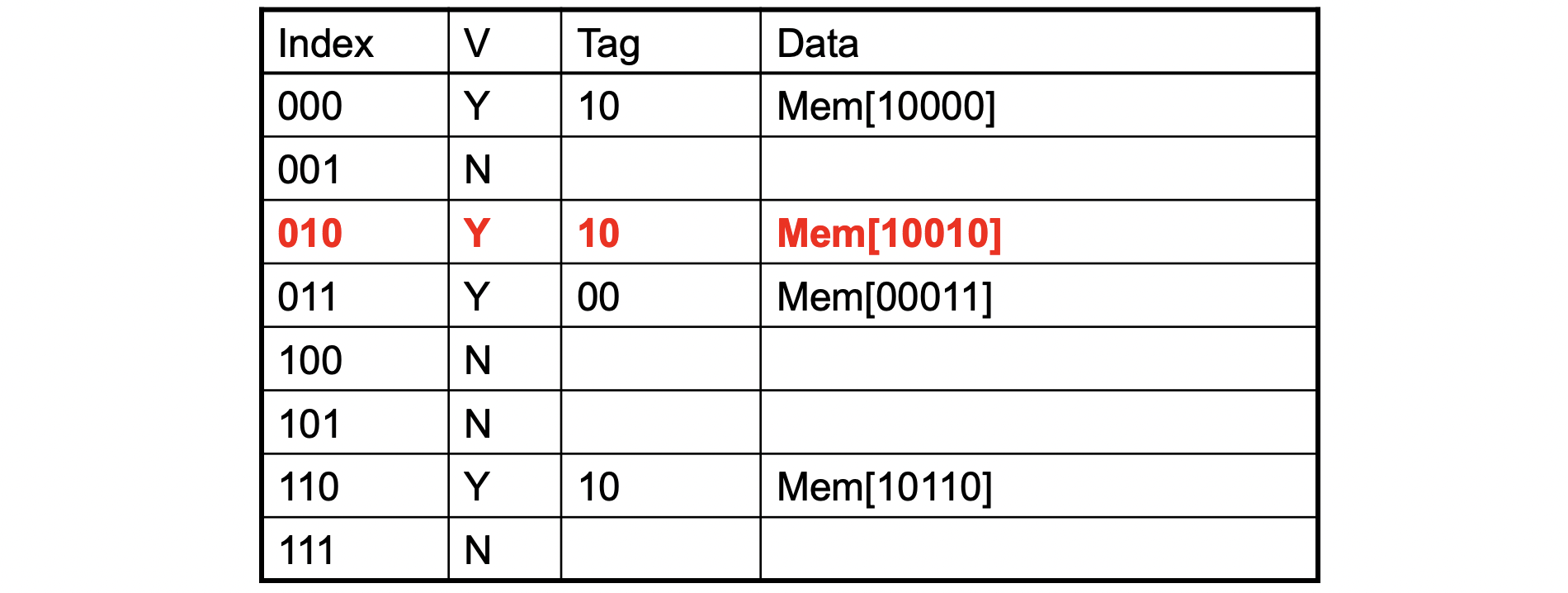

  

Address Subdivision

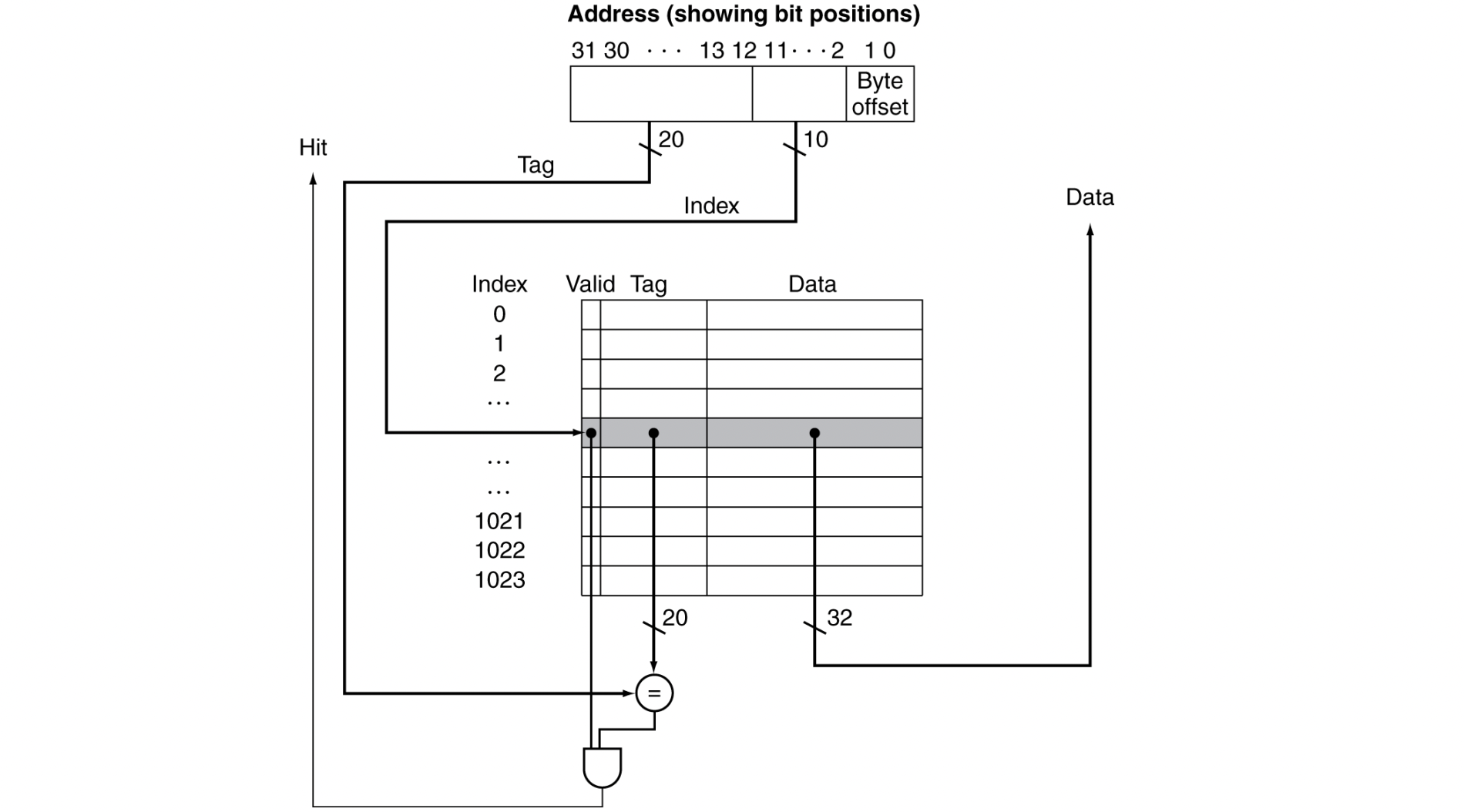
하나씩 천천히 살펴보자

1. 주어진 address는 32 bits이다.
   tag 20, index 10, byte offset 2
   - Tag : cache의 태그 필드 값과 비교하는데 쓰인다.
   - Index : 블록을 고르는 데 쓰인다. (cache내의 index 개수과 동일)
   - byte offset : 워드 내부의 바이트를 나타낸다(??) 블록 내의 워드를 선택할 때 이용x

2. 현재 캐시는 1024 word를 가진다. (1 word = 4 bytes)
   따라서 size of cache = 4 * 1024 bytes = 4KB
   (캐시 size를 계산할 때는 valid와 tag 부분을 무시한다)

3. 주어진 address 내의 Index field와 cache 내의 Index 번호를 비교해서 어느 위치에 가야하는지 찾는다.

4. Tag bit이 동일하고, Valid bit이 켜져 있으면 Hit
   그렇지 않으면 Miss

---

Example : Larger Block Size

• 64개의 block이 있고, 한 block당 16bytes의 크기를 갖는 캐시가 있다.
  byte 주소 1200이 mapping되는 block number는 몇인가?

• 1200 = 1 001011 0000
  

=> 001011 = 11

---

Block Size Considerations

• Larger block은 miss rate를 줄여준다.
  • Due to spatial locality
  • Once you have miss, you bring large words

• 하지만 cache의 size가 fixed라면,
  cache 내에 전체 블록의 수가 작아진다.
  • 그럼 블록 내의 많은 word가 access되기도 전에, 블록들이 cache에서 방출될 수가 있다.
  • 결국 miss rate가 올라간다

• 큰 miss penalty가 발생한다
  (How long it takes to bring data from memory to cache)
  • 결국 miss rate를 감소했던 이익보다 손해가 더 커질 수 있다.
  • Early restart and critical-word-first can help

---

Cache Misses

• Cache Hit에서는, CPU가 정상적으로 작동한다.

• Cache Miss에서는,

  • CPU pipeline을 stall시킨다
  • fetch block from next level of hierarchy
  • *Instruction cache miss
    • Restart instruction fetch
  • Data cache miss
    • Complete data access

---

Write-Through

• store 명령어에서, 데이터를 data cache에만 쓰고 main memory에는 쓰지 않은 경우, 메인 메모리와 캐시는 서로 다른 값을 가지게 된다. (inconsistent)
• 이 둘의 값을 일치시기는 방법은 항상 데이터를 메모리와 캐시에 같이 쓰는 것이다.
• Write through : also update memory

• 이 방식은 좋은 성능을 제공하기가 어렵다.
  모든 write가 메인 메모리에 데이터를 써야만 하기 때문이다.
  최소한 100개의 clock cycle이 필요하게 되면, 성능이 심하게 저하된다.

• 예를 들어, 기본 CPI = 1이고, 저장 명령어가 명령어의 10%를 차지하고, 매 write마다 100개의 추가 cycle이 필요하다면,
  CPI = 1 + 100 * 0.1 = 11.
• 즉, 약 10배의 성능 저하가 생긴다.

• 이를 해결하기 위한 방법은 write buffer를 이용하는 것이다
  • 메모리에 쓰이기 위해 기다리는 동안 데이터를 저장한다.
  • 캐시와 버퍼에 데이터를 쓰고 난 후, 프로세서는 수행을 계속한다.
  • 메인 메모리에 쓰기를 완료하면, 버퍼는 다시 빈다
  • 만약 버퍼가 모두 차 있으면 stall이 걸려야 한다.

---

Write-Back

• (교재)
  쓰기가 발생했을 때 새로운 값은 캐시 내의 블록에만 쓴다.
  나중에 캐시에서 쫒겨날 때 쓰기에 의해 내용이 바뀐 블록이면 낮은 계층에 써진다.
  메인 메모리의 처리 속도보다 프로세서가 쓰기를 더 빠르게 발생시키는 경우에 성능 향상이 가능하다.

• (필기)
  data write가 hit일 때, 일단 cache block만 update한다.
  dirty bit을 확인한다
  cache block의 값이 변경되면 dirty bit을 설정해준다.
  dirty bit을 확인해서 메모리에 쓸지 말지를 결정한다.

• (GPT)
  Dirty bit이 설정되어 있다면, 변경된 데이터를 메모리로 쓰여져야 하므로 메모리에 업데이트된 값을 전송합니다. Dirty bit이 설정되어 있지 않다면, 메모리로의 쓰기가 필요하지 않으므로 캐시 블록을 그대로 유지합니다.

---

Write Allocation

read Miss

• always allocate block

write Miss

Alternatives for write-through

• allocate block (fetch the block)
  or
• write to memory directly (write around) (don't fetch the block)
  • 때때로 프로그램이 읽기도 전에 모든 블록을 쓰기 때문

---

Example : Intrinsity FastMATH 프로세서

• Embedded MIPS processor이다
  • 12단계 pipeline으로 구성된다
  • 각 cycle에서 instruction and data access가 발생한다

• Split cache : 분리된 I-cache와 D-cache를 사용한다
  • 각 cache는 16KB이고, 16word 크기의 블록을 갖는다.
    (16KB = 256 blocks * 16word / block) (???)

• miss rate
  • I-cache : 0.4%
  • D-cache : 11.4%
  • Weighted average : 3.2%
    (I-cache와 D-cache의 조합에 대한 유효 실패율)

• 작동 과정
  
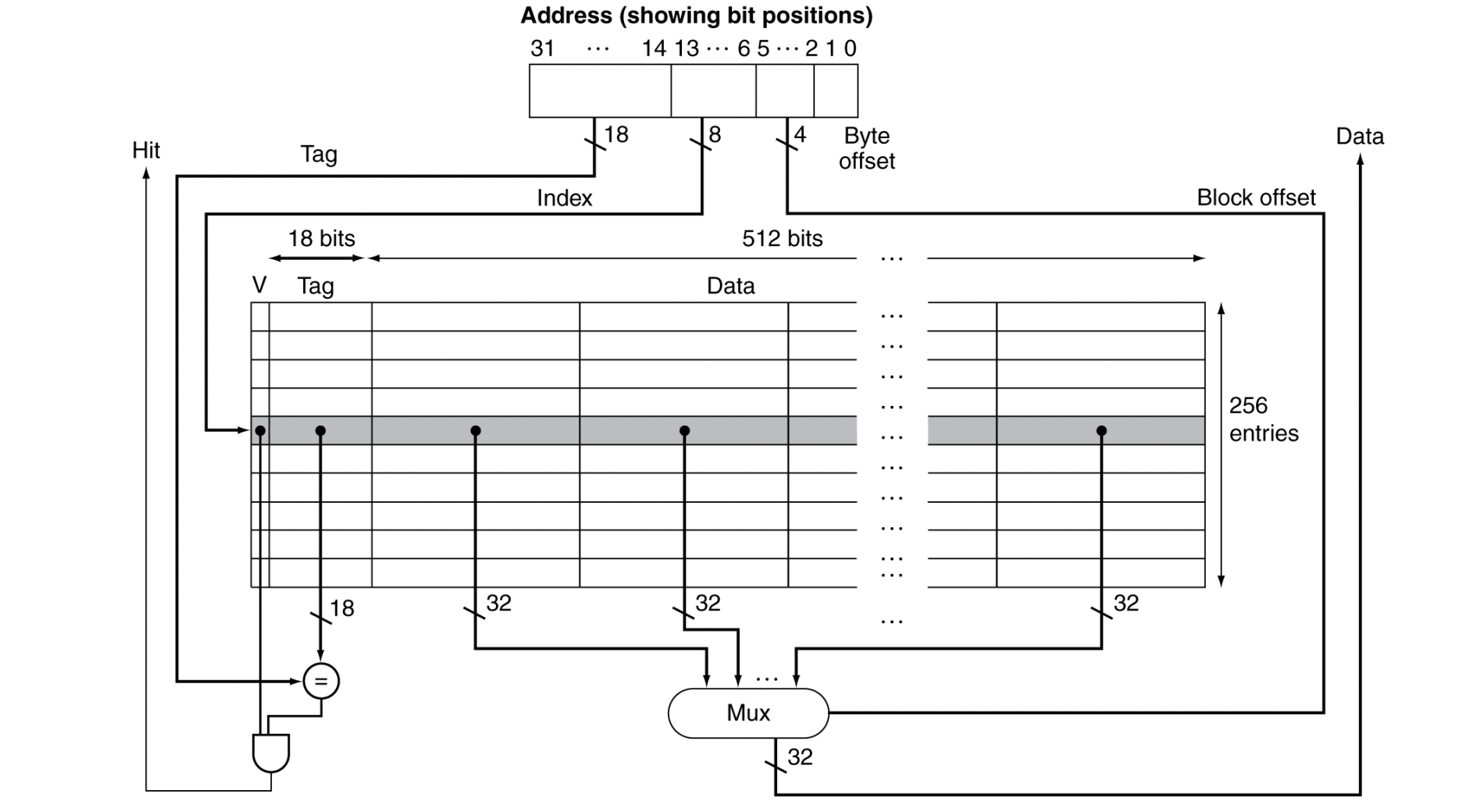
  • Index가 8bit이므로, 총 256개의 block을 갖는다
  • 각 block의 Data 부분은 총 16개의 워드가 존재한다.
    어느 워드를 가져와야 하는지는 block offset이 결정한다.
    따라서 block offset이 4 bit임을 확인할 수 있다.
    16 to 1 Mux를 이용한다.

---

Main Memory Supporting Caches

• Main memory로는 DRAM을 사용한다
  • Fixed width
  • Connected by fixed-width clocked bus
    • bus clock은 일반적으로 CPU clock보다 느리다.

• Example cache block read
  • 1 bus cycle for address transfer
  • 15 bus cycle per DRAM access
  • 1 bus cycle for data transfer

• For 4-word block, 1-word-wide DRAM
  • Miss penalty = 1 + 4*15 + 4*1 = 65 bus cycles
    • you need to fetch 4 word.
      each word you reading from main memory,
      15 bus clock cycle -> 4 words => 4 * 15
      4 word back to cache => 4 * 1
      (bus clock cycle ≠ CPU clock cycle)
  • Bandwidth
    (throughput : How many bytes you transfer over a period of time)
    = 16 bytes / 65 cycles = 0.25 B/cycle

Increasing Memory Bandwidth

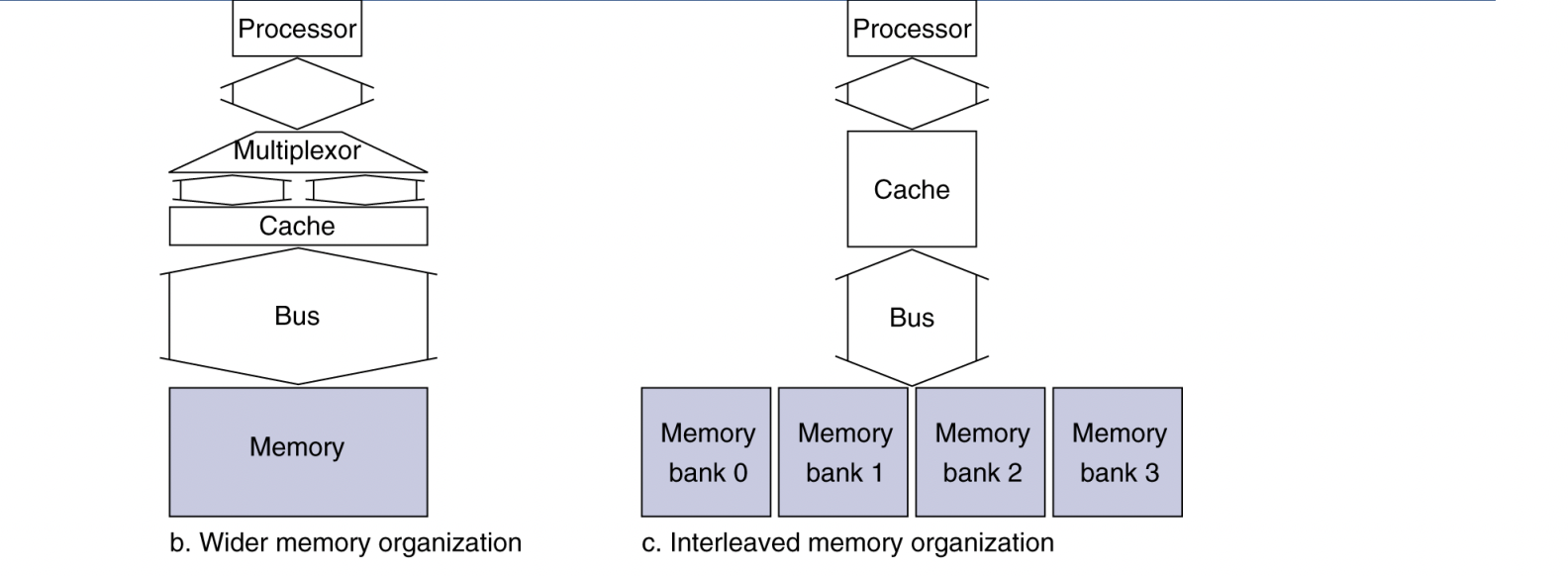
(b). 4-word wide memory

• Miss penalty = 1 + 15 + 1 = 17 bus cycles
  • Once you read, give 4 words
• Bandwidth = 16bytes / 17 cycles = 0.94 B/cycle

(c). 4-bank interleaved memory

• Miss penalty = 1 + 15 + 4 * 1 = 20 bus cycles
  • if i send address, go to 4 different banks in parallel,
    then get 4 word in parallel
  • 4 words in sequence (word back to 1-1)
• Bandwidth = 16 bytes / 20 cycles = 0.8 B/cycle

---

Measure Cache Performance

Components of CPU time

• Program execution cycles
  • cache hit time을 포함한다
• Memory stall cycles
  • 주로 cache miss

Memory stall cycles
= (Memory accesses/Program) * Miss rate * Miss penalty
= (Instructions/Program) * (Misses/Instructions) * Miss penalty

Example

I-cache miss rate = 2%, (it's for every instructions)
D-cache miss rate = 4%, (it's only for lw/sw instructions)
Miss penalty = 100 cycles,
Base CPI (ideal cache) = 2, (Don't have cache miss at all)
Load & store are 36% of instructions.

• Miss cycles per instruction
  • I-cache = 0.02 * 100 = 2
  • D-cache = 0.04 0.36 100 = 1.44

• Actual CPI = 2 + 2 + 1.44 = 5.44
  Ideal CPI is 2.72(5.44/2) times faster

Average memory access time (AMAT)

= Hit time + Miss rate * Miss penalty

Example

CPU with 1ns clock,
hit time = 1cycle,
miss penalty = 20 cycles,
I-cache miss rate = 5%

• AMAT = 1 + 0.05 * 20 = 2ns
  (2 cycles per instruction)

---

Summary

• CPU 성능이 향상될 때, Miss penalty는 더더욱 중요해진다
• base CPI가 줄어들면 memory stall에 쓰이는 시간이 큰 비중을 가진다
• clock rate가 커지면 CPU cycle에서 memory stall이 큰 비중을 가진다
• system performance를 평가할 때 cache behavior를 무시할 수 없다.