[자료구조/알고리즘] 시간 복잡도

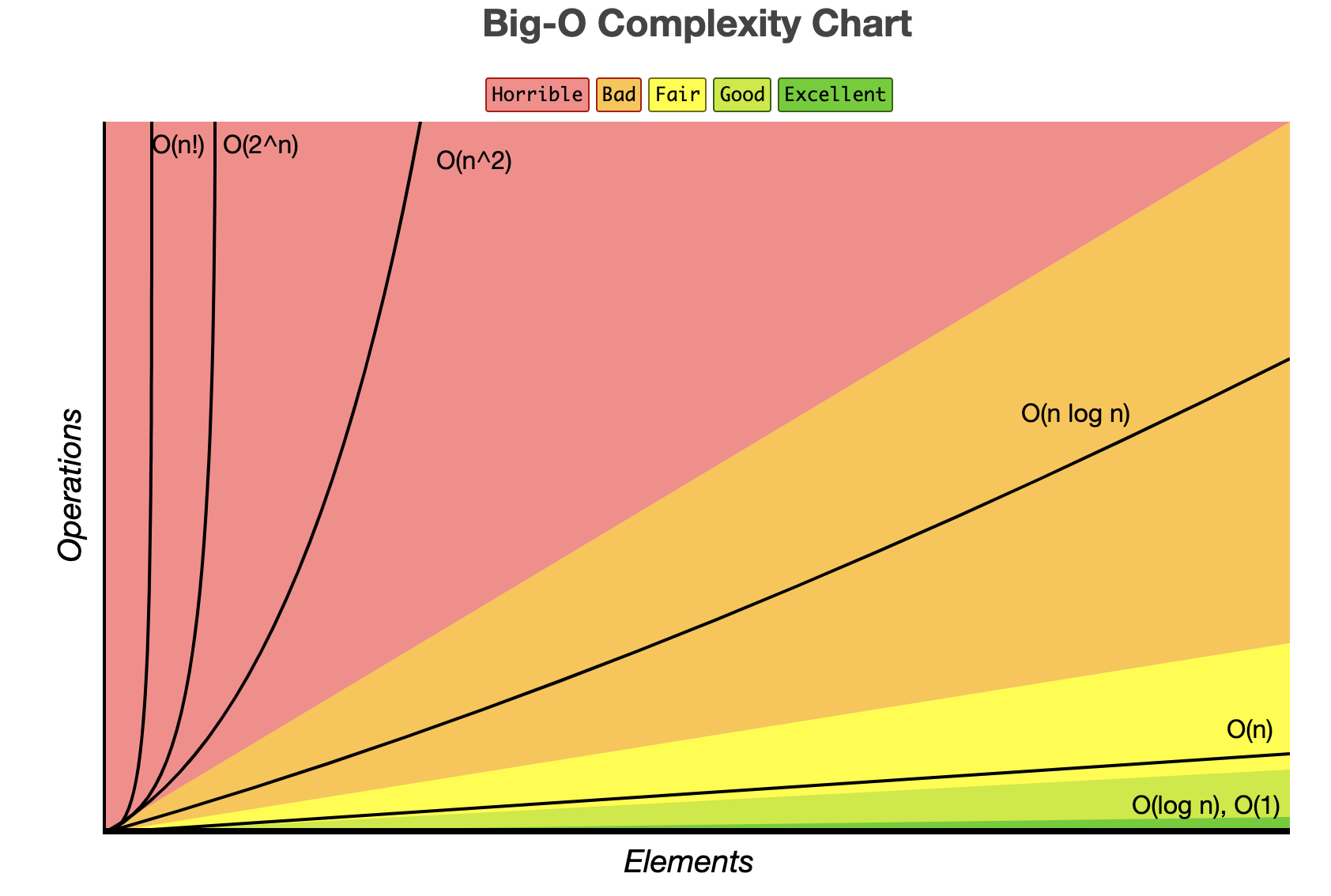
시간복잡도

알고리즘 문제를 풀 때 효율적인 방법을 고민하기 위해 고려해야할 조건 중 하나는 시간 복잡도이다. 시간 복잡도를 고려한다는 것은 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼만큼 걸리는지를 확인한다는 것이다. 즉, 입력값이 커짐에 따라 증가하는 시간의 비율이 최소화될 수록 효율적인 알고리즘을 구현했다고 할 수 있다.

대부분 Big-O 표기법으로 시간 복잡도를 나타낸다. Big-O 표기법은 최악의 경우를 나타내므로, 만약 연산에 최대 1시간이 걸릴경우, Big-O 표기법으로 해당 연산은 1시간짜리 시간복잡도를 가진 연산이라고 본다.

O(1)

: 입력값의 크기와 상관 없이 즉시 출력값을 알 수 있는 시간 복잡도

function algorithm(arr,idx) {
  return arr[idx];
}
// arr의 크기가 아무리 커져도 출력값을 바로 얻어낼 수 있다.
// arr의 길이가 1일때나 1000000일때나 리턴값을 얻는데는 똑같은 시간이 소요된다.

O(n)

: 입력값이 증가함에 따라 시간도 같은 비율로 증가하는 시간 복잡도 - linear complexity
입력값의 크기가 1일때 어떤 연산에 1초의 시간이 걸리고 크기가 100일 때 100초의 시간이 걸렸다면 O(n) 시간 복잡도를 가진다고 본다.

//입력값이 1 증가할 때, 실행시간은 1초씩 증가
//입력값 크기:1 -> 1초
//입력값 크기:2 -> 2초
//입력값 크기:100 -> 100초
function O_N_algorithm(n){
  for(let i=0;i<n;i++){
    //연산 시 1초의 시간이 걸림
  }
}
//입력값이 1 증가할 때, 실행시간은 2초씩 증가
//입력값 크기:1 -> 1초
//입력값 크기:2 -> 4초
//입력값 크기:100 -> 200초
function O_2N_algorithm(n){
  for(let i=0;i<2n;i++){
    //연산 시 1초의 시간이 걸림
  }
}

두번째 코드 예시의 경우 O(2n)으로 생각할 수도 있지만, 입력값의 크기가 커질 수록 계수의 의미는 크게 영향을 미치지 않기 때문에, 같은 비율로 증가한다면 모두 O(n) 시간 복잡도를 가진다고 본다.

O(logn)

: 입력값의 크기가 커질수록 logn에 비례하여 증가하는 시간 복잡도 - logarithmic complexity
이진 검색과 같이 입력값의 크기에서 특정 값을 찾을 때까지 절반씩 줄여나가는 연산을 가질 경우 O(logn)의 시간 복잡도를 가진다.

//N(입력값의 크기)을 2번 나누기 k번 실행으로 1이 될때까지 연산
//2^k = N  ->  log2N 
function binarySearch(n, arr, start, end){
  if(start>end){
    return -1;
  }
  let idx = parseInt((start+end)/2);
  if(arr[idx] === n) {
    return idx;
  }else if(arr[idx] > n) {
    //찾고자 하는 숫자가 배열의 반절의 값보다 작을 때
    return binarySearch(n, arr, start, idx-1);
  }else{
    //찾고자 하는 숫자가 배열의 반절의 값보다 클 때
    return binarySearch(n, arr, idx+1, end);
  }
}

또 다른 예제로는,

for(let i=0;i<n;i++){
  i *= k;
}
//k배수만큼 i가 증가하며 n으로 도달
//k^i === n  -> log(k) n 

O(n^2)

: 입력값의 크기가 커질수록 시간이 n의 제곱수의 비율로 증가하는 시간 복잡도 - quadratic complexity
입력값의 크기가 1일때 어떤 연산에 1초의 시간이 걸리고 크기가 5일 때 25초의 시간이 걸렸다면 O(n^2) 시간 복잡도를 가진다고 본다.

//입력값이 1 증가할 때, 실행시간은 1초씩 증가
//입력값 크기:1 -> 1*1 = 1초
//입력값 크기:2 -> 2*2 = 4초
//입력값 크기:100 -> 100*100 = 100초
function O_quadratic_algorithm(n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
		// do something for 1 second
		}
	}
} 
//n^3씩 실행시간 증가
function another_O_quadratic_algorithm(n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
			for (let k = 0; k < n; k++) {
			// do something for 1 second
			}
		}
	}
}

O(2n),O(3n)이 O(n)과 같은 시간 복잡도로 표기되는 것과 마찬가지로 n^2과 n^3, n^4, n^5 모두 O(n^2)로 표시한다.

O(2^n)

: 입력값의 크기가 증가함에 따라 매번 2배씩 시간이 늘어나는 시간 복잡도 - exponential complexity

//재귀로 구현하는 피보나치 수열 
//n이 100이상 넘어갈 경우 평생 결과값을 못받을 수도 있다.
function fibonacci(n) {
	if (n <= 1) {
		return 1;
	}
	return fibonacci(n - 1) + fibonacci(n - 2);
}

시간복잡도의 빠른 순서대로 비교를 하자면
: O(1) < O(logn) < O(n) < O(n^2) < O(2^n)