Hash Table
키-값쌍으로 데이터를 저장하는 자료구조- 키를 해시 함수를 이용해 고정된 크기의 숫자로 변환하고, 이를 배열의 인덱스로 사용해서 데이터를 저장하고 검색한다.
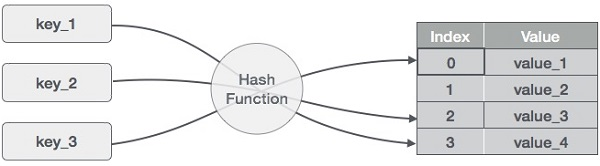
시간 복잡도
- 삽입 : O(1)
- 삭제 : O(1)
- 검색 : O(1)
하지만, 해시 충돌(hash collision)이 발생하는 경우에는 O(n)의 시간 복잡도를 가질 수 있으므로 충돌을 최소화하고자 하는 노력이 필요하다.
B+ Tree
- 많은 양의 데이터를 저장하고 검색하는 데 사용되는 자료구조
키-값쌍으로 이루어진 레코드를 leaf node에 저장하고, 내부 node에는 leaf-node의 범위를 나타내는 키만 저장한다.- 균형 잡힌 트리(balanced tree)로서, 모든 리프 노드가 같은 깊이에 위치하도록 유지되는 특성 때문에, 특정 키 값을 검색할 때 최악의 경우에도 O(log n)의 시간 복잡도를 가진다.
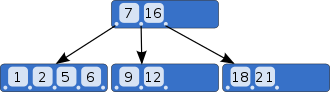
-> 루트 노드부터 시작하여 각 레벨을 내려가며 탐색한다.균형잡힌 특성을 유지하기 때문에 탐색 경로가 균등하게 분산되어 탐색속도가 빠르다.
시간 복잡도
- 검색 : O(log n)
- 삭제 : O(log n)
- 삽입 : O(log n)
그럼 hash table의 시간복잡도가 b+tree의 시간복잡도보다 더 빠른데 왜 index는 b+tree로 구현될까?
- 범위 검색과 같은 부등호 연산에서는 매우 비효율적
Hash table을 사용하면 하나의 데이터를 탐색하는 시간, 즉 등호 연산을 수행하는 시간은 O(1)로 b+tree보다 빠른 성능을 보이지만, 값이 정렬되어 있지 않기 때문에 범위 검색과 같은 부등호 연산에서는 매우 비효율적이다. - 해시 충돌
해시 테이블은 해시 충돌이 발생하면 O(n)의 시간 복잡도를 가질 수 있다. 해시 충돌을 최소화한다고 해도, 최소화하기 위해 일반적으로 더 큰 공간을 할당하기 떄문에, 메모리 사용량이 크게 증가할 수 있다.
해시 충돌은 서로 같은 데이터나 다른 데이터가 동일한 해시값을 갖게 되어 충돌이 발생하는 상황을 의미한다. 이런 경우에는 해시 충돌을 해결하기 위한 다양한 방법을 사용해야 하고(rehashing등), 이러한 방법들은 처리 과정에서 O(n)의 시간 복잡도를 가질 수도 있다.
반면에, B+Tree는 데이터의 분포에 영향을 덜 받고, 균형잡힌 트리 구조를 가지므로 최악의 경우에도 O(log n)의 검색, 삽입, 삭제 시간 복잡도를 보장한다. - 이외에도 b+tree가 병행성 제어에 좀 더 적합한 구조
데이터베이스에서는 다수의 사용자가 동시에 데이터에 접근하고 작업할 수 있어야 해서 병행성 제어와 같은 기능이 필요한데, b+tree는 이러한 병행성 제어를 지원하는 데에 더 적합한 구조이다. 예를 들어, 트랜잭션이 특정 노드를 접근하면 그 노드와 그 자식 노드들만 lock을 걸어서 다른 트랜잭션의 접근을 제한할 수 있다.
