Definition Access
- 이진 탐색
- 선택정렬
- 퀵정렬
Mechanism
1.이진탐색
이진 탐색이란 이름이 붙여진 이유는 처음에 N개 크기의 배열에서 단계가 하나씩 지나감에 따라 탐색할 배열의 크기가 반씩 줄어들기 때문이다.
이진 탐색 예시
오름차순으로 정렬된 배열이 있다.
{ 17, 28, 43, 67, 88, 92, 100 }
이 배열에서 이진 탐색을 이용하여 43의 값을 찾아보자.
첫 번째 시도
우선 가운데에 위치한 임의의 값 67을 선택한다.
선택한 값 67과 찾고자 하는 값 43를 비교한다.
43 < 67 이므로 43은 67의 좌측에 존재한다는 것을 알 수 있다.
두 번째 시도
67을 기준으로 좌측에 있는 배열 값들을 대상으로 다시 탐색을 진행한다.
{ 17, 28, 43 }
마찬가지로 가운데의 임의의 값 28을 선택한다.
28 < 43 이번에는 28이 43보다 작으므로 28 우측에 위치하는 것을 알 수 있다.
세 번째 시도
28의 우측을 기준으로 배열을 다시 설정해보면
{ 43 }
배열에 값이 하나만 남게 되고 값을 확인해보면,43 == 43 원하는 값을 찾았다.
출처 : https://cjh5414.github.io/binary-search/
2. 선택 정렬(Selection sort)
: 여러 데이터들중 가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸고, 그다음 작은 데이터를 선택해 앞에서 두 번째 데이터와 바꾸는 과정을 반복하는 것
-
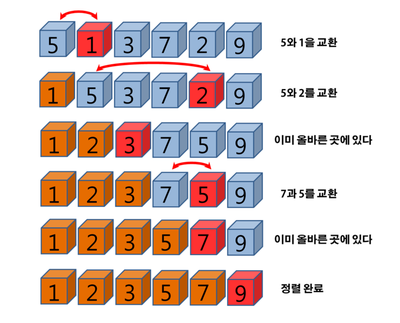
처음에는 정렬되어 있지 않으므로 가장 작은 1을 선택해서 맨앞의 숫자인 5와 swap
-
맨앞의 1을 제외하고 나머지 숫자들 중에서 가장 작은 2를 선택해서 맨앞의 숫자인 5와 swap
-
맨앞의 1, 2를 제외하고 나머지 숫자들 중에서 가장 작은 3을 선택해서 맨앞의 숫자인 3과 swap(이미있다.)
-
맨앞의 1, 2, 3을 제외하고 나머지 숫자들 중에서 가장 작은 5를 선택해서 맨앞의 숫자인 7과 swap
-
맨앞의 1, 2, 3, 5를 제외하고 나머지 숫자들 중에서 가장 작은 7을 선택해서 맨앞의 숫자인 7과 swap(이미있다.)
-
맨앞의 1, 2, 3, 5, 7을 제외하고 나머지 숫자는 9 하나 이므로 swap 안해도된다. (이미있다.)
- 이미 하나 남은 것은 swap할 필요가 없으므로
이처럼 선택정렬은 가장작은 데이터를 앞으로 보내는 과정을 N - 1번 반복하면 정렬이 완료된다.
출처 : https://doodreamcode.tistory.com/52
3. 퀵 정렬
-
퀵 정렬(Quick sort)
퀵 정렬은 평균적으로 매우 빠른 속도를 자랑하는 정렬 방법이다. -
그렇기에 이름부터가 다소 건방진 '퀵' 정렬인데 보통 다른 정렬 방법들은 이름으로부터 어떻게 정렬을 하는지 유추할 수 있다. 선택 정렬은 최솟값을 찾아 선택한다고 해서 선택 정렬이라든지, 병합 정렬은 병합하면서 정렬한다고 해서 병합 정렬이라든지, 퀵 정렬을 그런 방식으로 이름을 바꾸면 피벗 정렬(pivot sort)이 될 것이다. 퀵 정렬은 피벗을 기준으로 목록을 큰 값과 작은 값으로 나누어 가며 정렬하기 때문이다.
-
실제 알고리즘을 보면서 어떻게 정렬을 하는지 살펴보자.
-
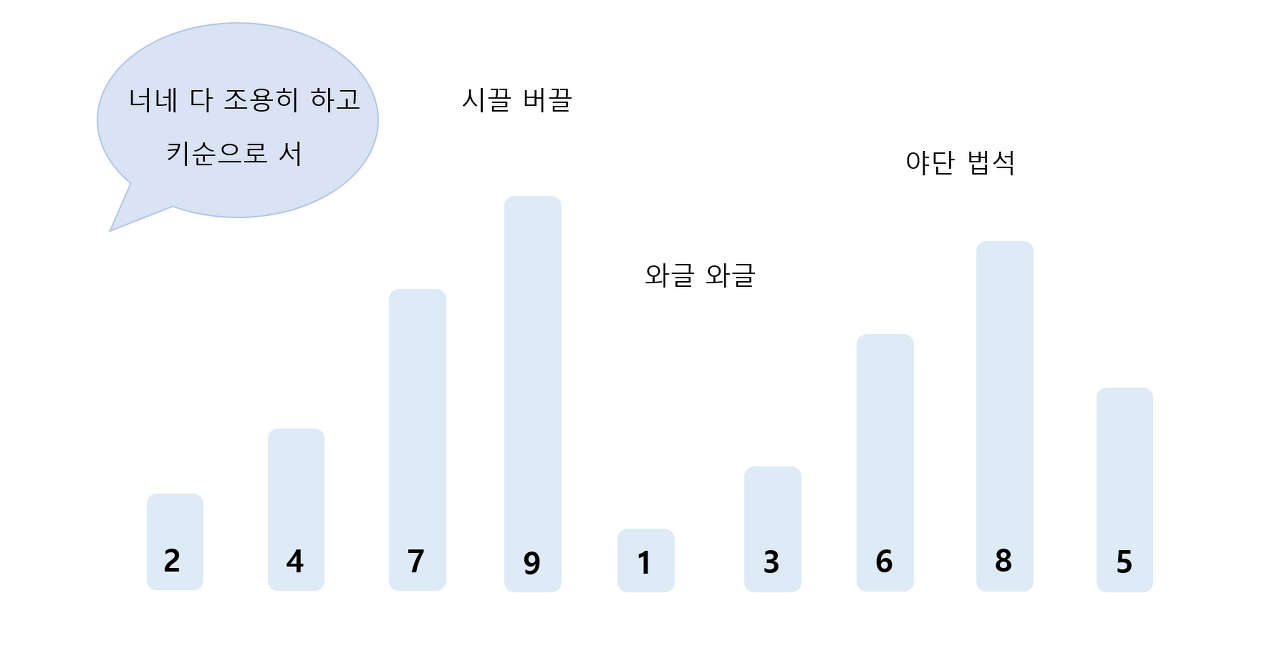
실생활의 예를 들어보려 합니다. 9명의 학생이 운동장에 떠들고 있으니 선생님이 한 마디 한다.
-
학창 시절 선생님이 키순으로 서라고 하면 어떻게 했는지 기어가는가? 대충 크다 싶으면 뒤로 가고 작다 싶으면 앞으로 가면서 섰던 거 같다. 하지만 이번엔 퀵 정렬 방식으로 키순으로 서보려 한다.
-
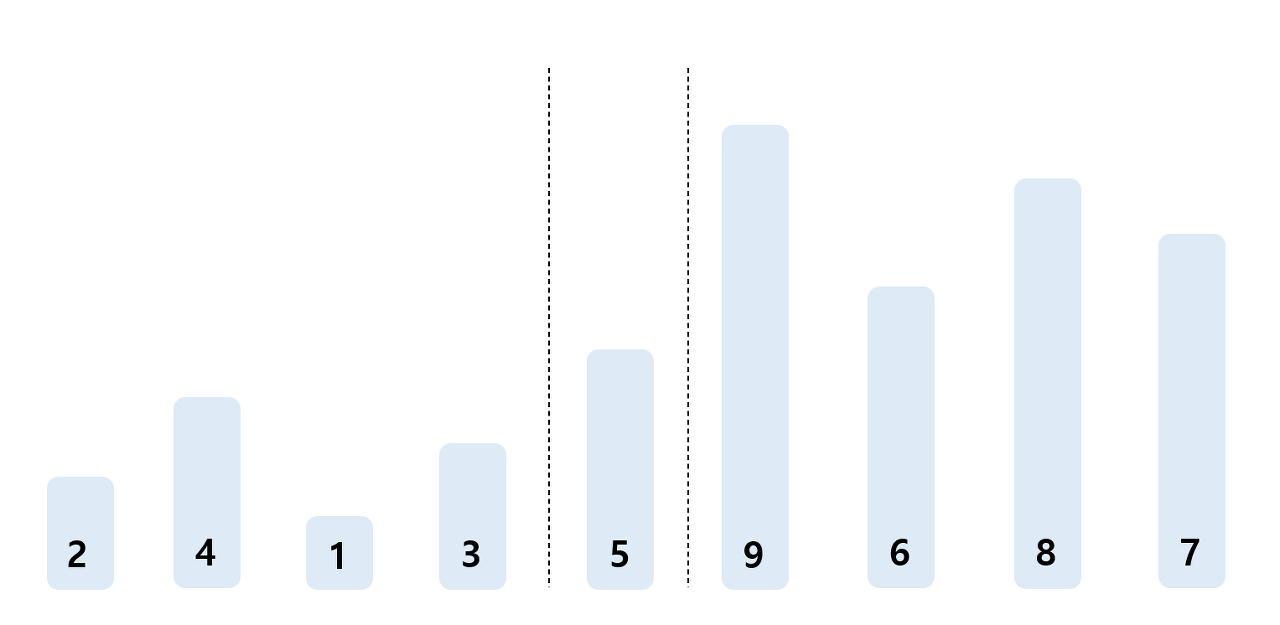
시끄럽던 와중에 제일 뒤에 서 있던 친구가 Pivot! (우리 말로는 기준! 이 되겠네요)을 외치며 자기보다 작은 사람은 자기 앞으로 가고 큰 사람은 자기 뒤로 가라고 한다.

- 5번 말을 듣고 난 결과이다. 5번이 똑똑한 친구인 게 5번은 말 한마디로 자기가 서야 될 위치를 찾았다. 5번은 자기 위치를 찾았으니 가만히 있으면 된다.
-
하지만 5번만 좋은 건 아니다. 기존에는 9명의 친구들이 서로 키를 비교했어야 됐다면 이제는 5번 앞에 있는 친구들은 앞에 친구들끼리, 5번 뒤에 있는 친구들은 뒤에 친구들끼리 정렬하면 된다. 5번보다 작은 그룹과 5번보다 큰 그룹으로 나뉘게 된다.
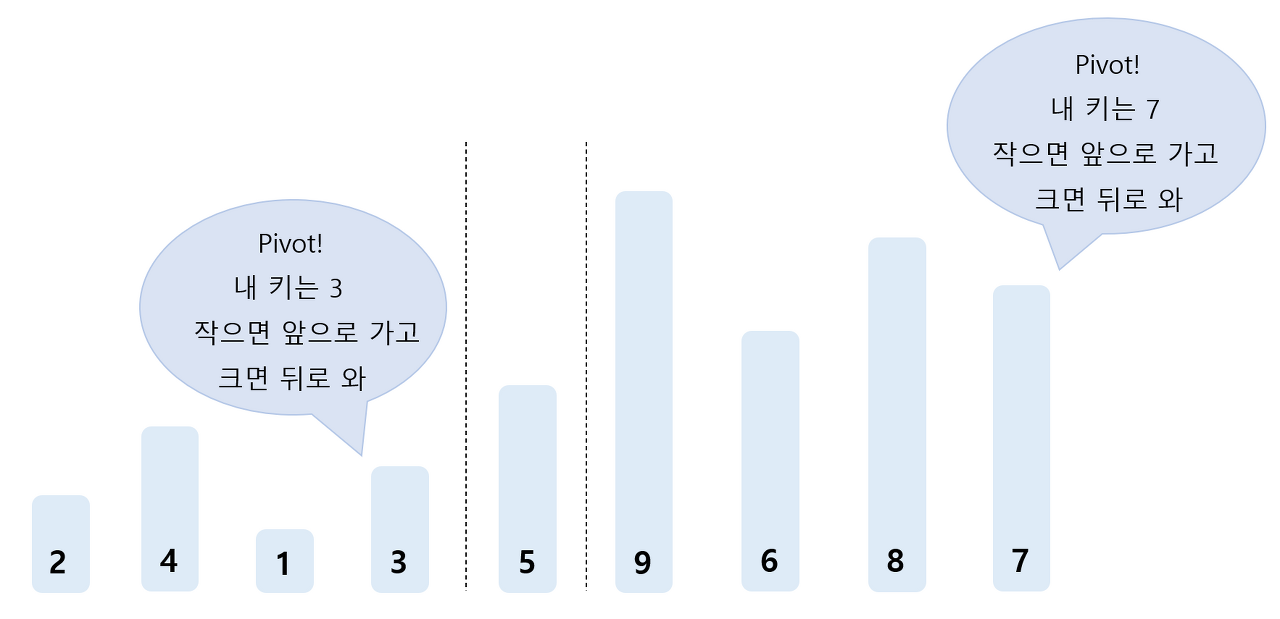
- 각 그룹에 제일 뒤에 서 있던 3번과 7번은 5번처럼 Pivot! 을 외치고, 각 그룹에서 3, 7 보다 작은 친구는 3, 7 보다 앞으로 가고 3,7 보다 큰 친구는 3, 7 보다 뒤로 가게 된다.
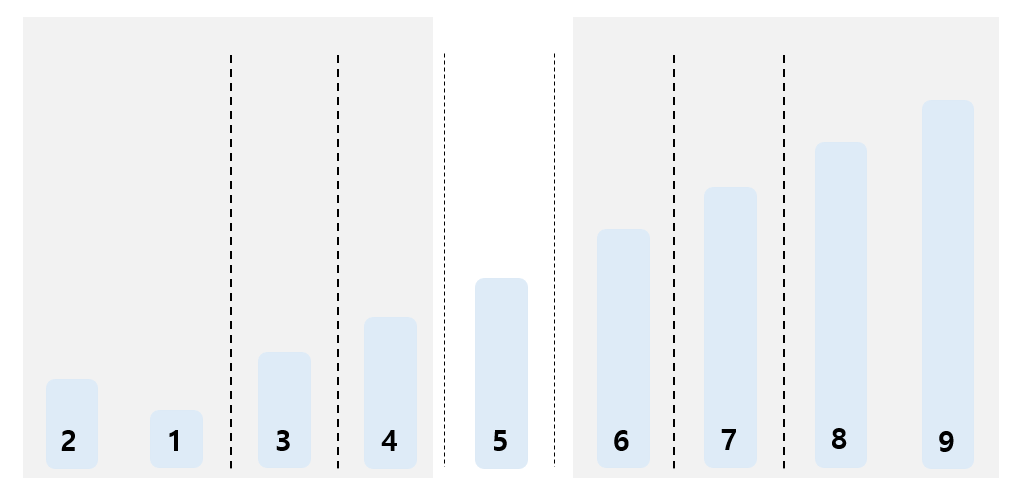
-
3번과 7번이 Pivot! 을 외친 결과 3번과 7번도 자기 자리를 찾았다. 이번에는 두 명의 학생이 자기 자리를 찾은 셈이다. 다음에 할 일이 예상되는가? 1~4번 그룹은 다시 두 그룹으로 나뉘었다. 아마 나뉜 두 그룹에서 마지막에 선 친구는 다시 Pivot! 을 외칠 것이다. 하지만 4번은 혼자 남게 되었으니 더 이상 Pivot! 을 외칠 필요가 없다.
-
마찬가지로 6~9번 그룹도 두 그룹으로 나뉘었다. 7보다 큰 그룹에는 두 명이 남았으니 마지막에 선 친구가 Pivot! 을 외치고 6번은 혼자 남았으니 외칠 필요가 없다.
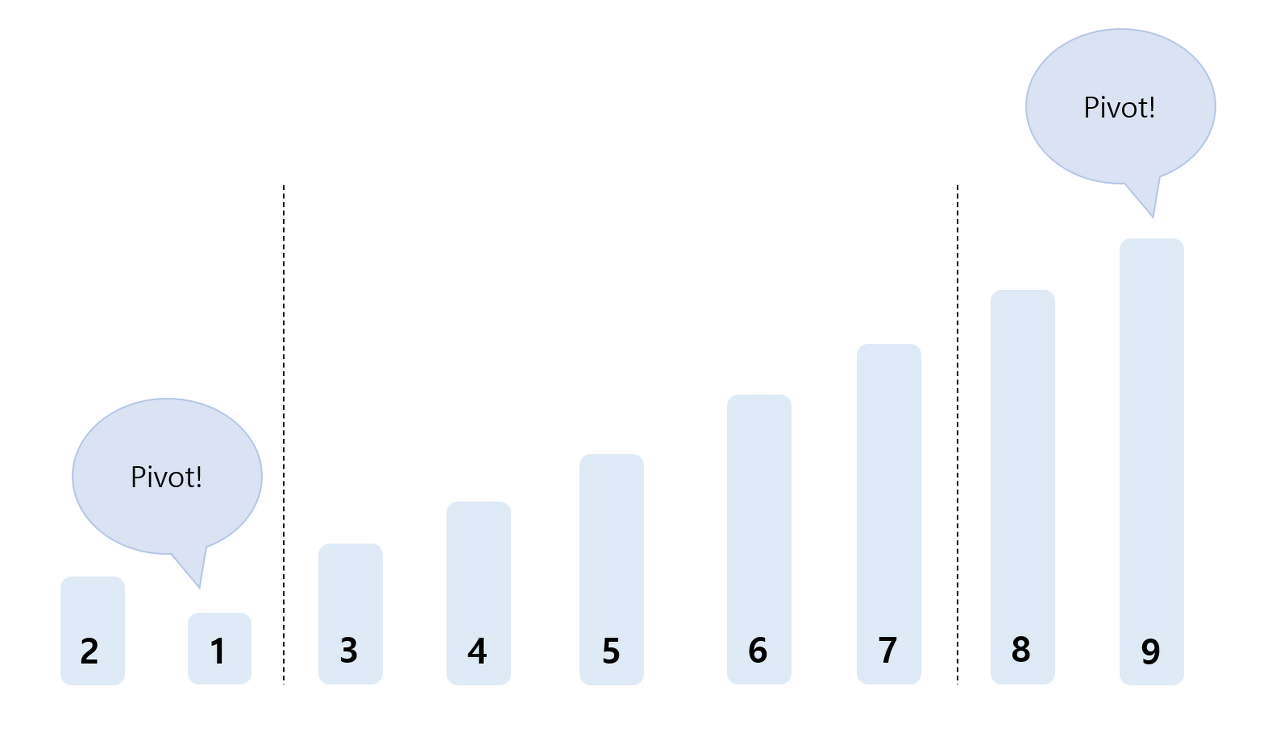
-
1과 9번이 Pivot!을 외치고, 9번은 이미 8번이 9번보다 작으니 가만히 있으면 되고 1번과 2번은 순서가 바뀌게 된다.

- 이렇게 되면 키순으로 정렬을 마치게 된다.(퀵정렬)
출처 : https://spacebike.tistory.com/29
Retrospection
- [소프트웨어] 20 ~ 21번 이진 탐색, 선택정렬, 퀵정렬 정리함.
