[알고리즘] 백준 11660 구간 합 구하기 5

https://www.acmicpc.net/problem/11660

누적합을 이용하는 DP 문제이다. 블로그 풀이들을 한참 보아도 이해가 가지 않다가 직접 그려보며 이해한 내용을 정리해보려한다.

만약 아래와 같이 2차원 행렬이 주어졌다고 해보자

1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7

그때 누적합은 아래 그림과 같이 그려지게 된다.

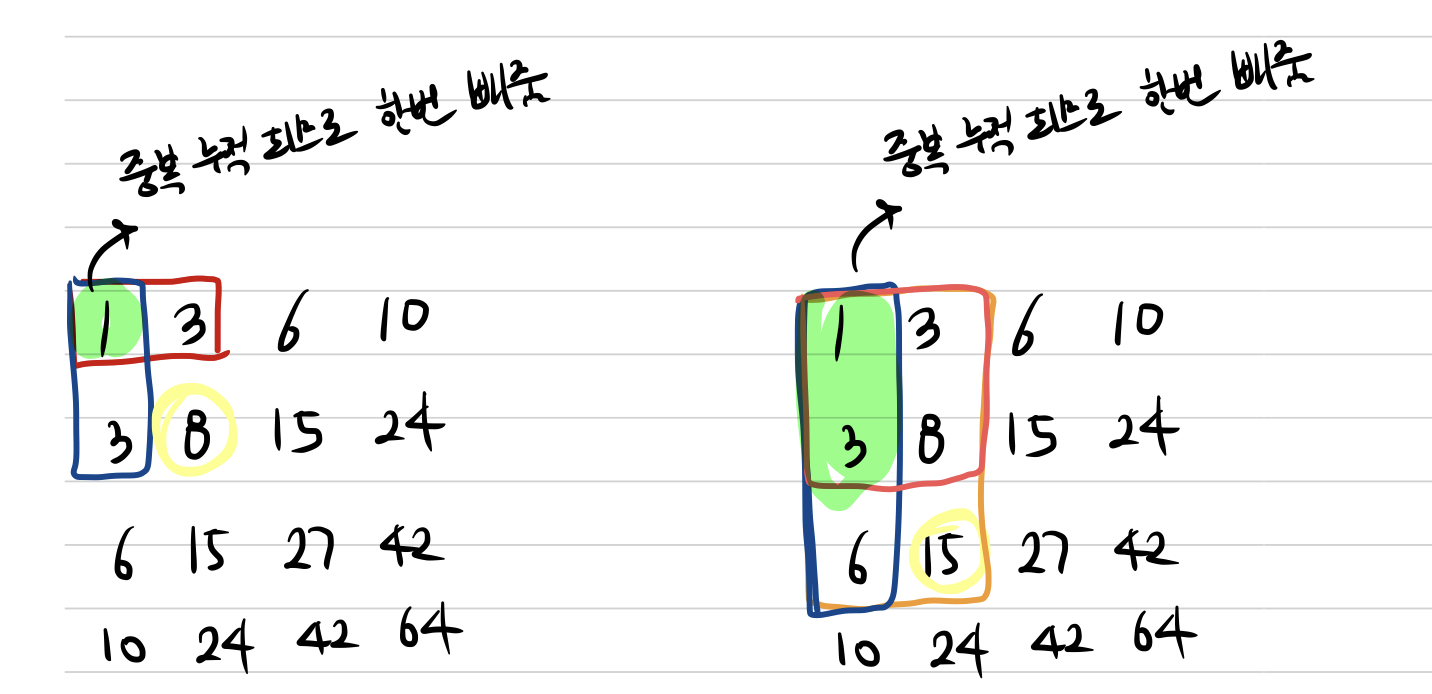
위 그림의 의미는 다음과 같다. (1,2)의 3은 (1,1)~(1,2)까지의 누적합을 의미하고, (2,1)의 3은 (1,1)부터 (2,1)까지의 누적합을 의미하게 된다. 그렇다면 (2,2)의 누적합을 구하기 위해서는 (1,2)와 (2,1)을 더하고 중복 합으로 들어가는 (1,1)의 값을 빼준 뒤에, 입력으로 주어진 행렬의 (2,2) 위치에 해당하는 3을 더해준다.

두번째 그림으로 이해하면 조금 더 이해가 쉽다.
만약 (3,2) 위치의 누적합을 구하고자 할 경우에는, 마찬가지로 해당 위치 전 위치들의 누적합에 주어진 입력 행렬에서의 현재 위치 (3,2)의 값인 4를 더해주면 된다.

이를 식으로 표현하면 다음과 같다. 누적 행렬을 표현하는 리스트를 dp라고 할때
dp[i][[j] = dp[i-1][j] + dp[i][[j-1] - dp[i-1][[j-1] + board[i][[j]

이 식을 이해하는데 까지 오랜 시간이 걸렸다..

이 식을 이용하여 AC를 받은 코드는 아래와 같다.

import sys

N, M = map(int, sys.stdin.readline().split())
board = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]

dp = [[0 for _ in range(N+1)] for _ in range(N+1)]

for i in range(1, N+1):
    for j in range(1, N+1):
        dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + board[i-1][j-1]

for _ in range(M):
    x1, y1, x2, y2 = map(int, sys.stdin.readline().split())
    result = dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1]
    print(result)