위상정렬
위상 정렬이란?
'순서가 정해져있는 작업' 을 차례로 수행해야 할 때 그 순서를 결정해주기 위해 사용하는 알고리즘이다.
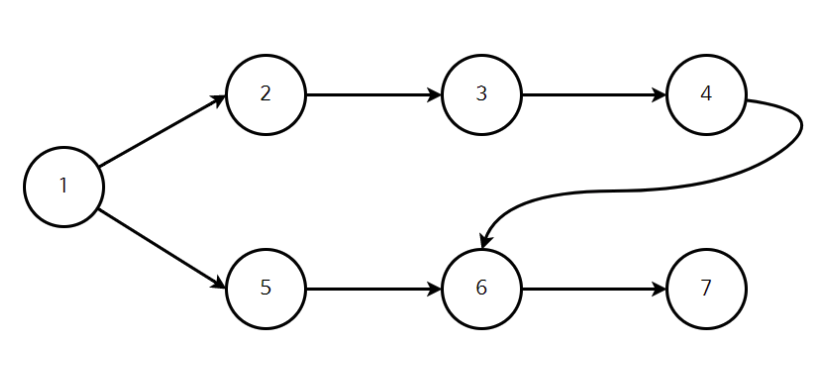
위 그림을 통해 알 수 있는 것은 6번 작업은 4번과 5번 작업 다음에 수행될 수 있다는 것이다. 이 처럼 순서가 정해져 있는 작업에 대해서 그 순서를 정렬해주는 알고리즘인것이다.
위상 정렬은 두 가지 해결책을 도출할 수 있다.
1. 현재 그래프가 위상 정렬이 가능한지
2. 가능하다면 정렬된 결과는 무엇인지
위상 정렬을 구현하는 방법은 스택(Stack)과 큐(Queue)모두 가능하지만, 보편적으로 큐를 많이 사용한다.
큐를 이용해 위상 정렬을 구현하는 방법
- 진입차수가 0인 정점을 큐에 삽입한다
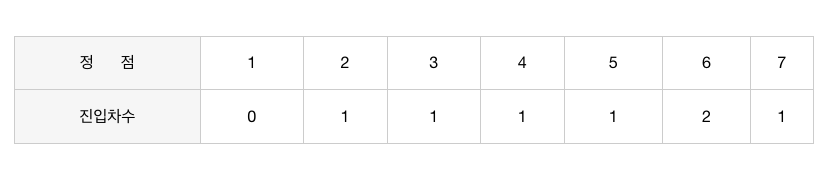
진입 차수란? : 각 정점으로 '들어오는' 간선의 개수를 의미한다. 위 예제에서는 1번의 진입차수는 0이며, 5의 진입차수는 1, 6의 진입차수는 2가 된다.
- 큐에서 원소를 꺼내 연결된 모든 간선을 제거한다. (=진입 차수를 -1 시켜준다)
- 간선 제거 이후에 진입 차수가 0이 된 정점이 있다면, 다시 정점을 큐에 삽입한다. (1번과 동일)
- 큐가 모두 비워질 때까지 위 과정을 반복한다. 모든 원소를 방문하기 전에 큐가 빈다면, 그래프에 사이클이 존재하는 것이고(= 위상 정렬이 불가능하다), 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상 정렬의 결과가 된다.
먼저 진입 차수를 리스트에 기록한다.
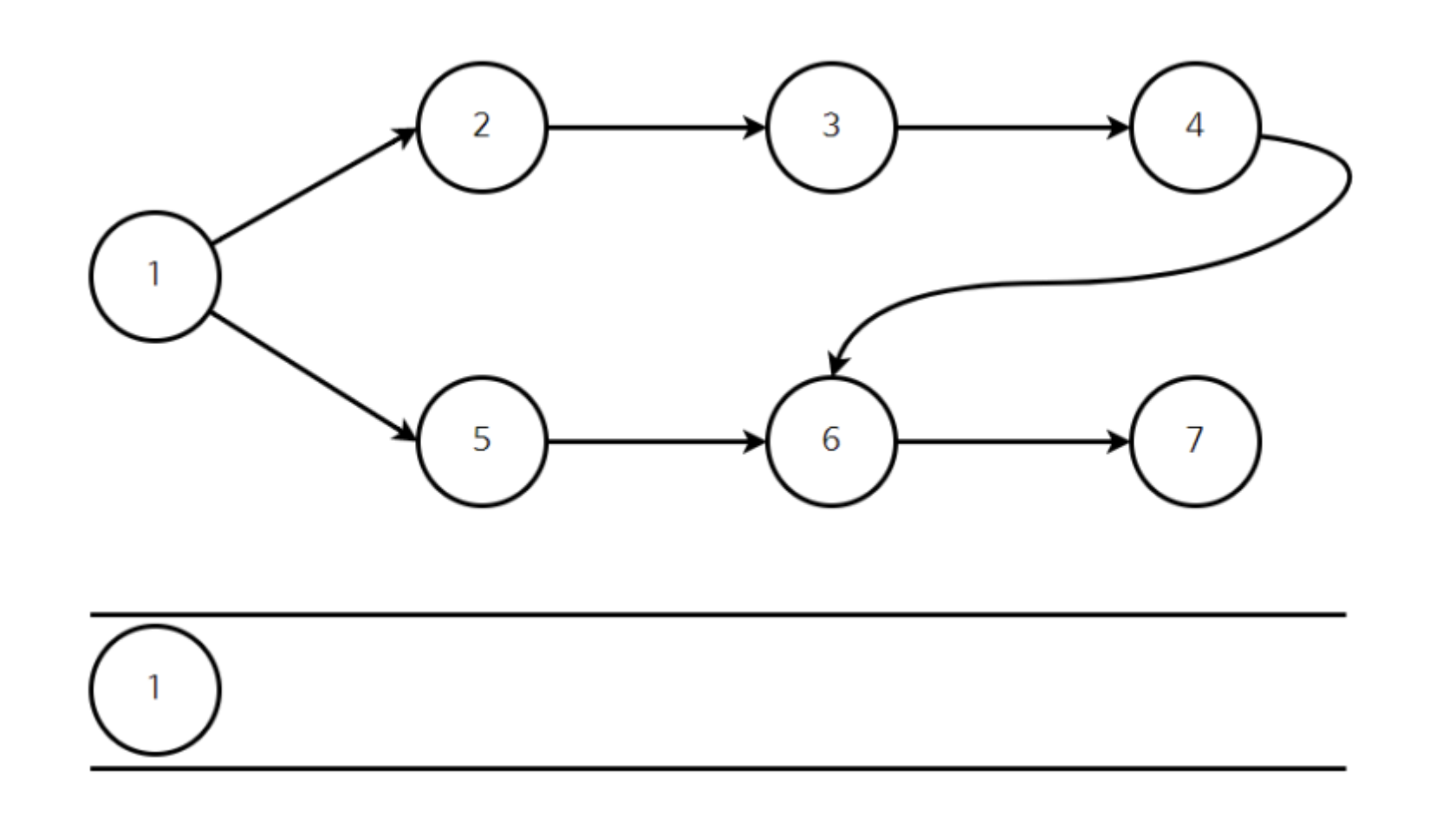
이후 진입 차수가 0인 정점 1번을 먼저 큐에 삽입한다.
큐에 정점을 삽입했다면, 정점과 연결된 간선들을 끊어준다 (= 진입차수를 -1 시켜준다).
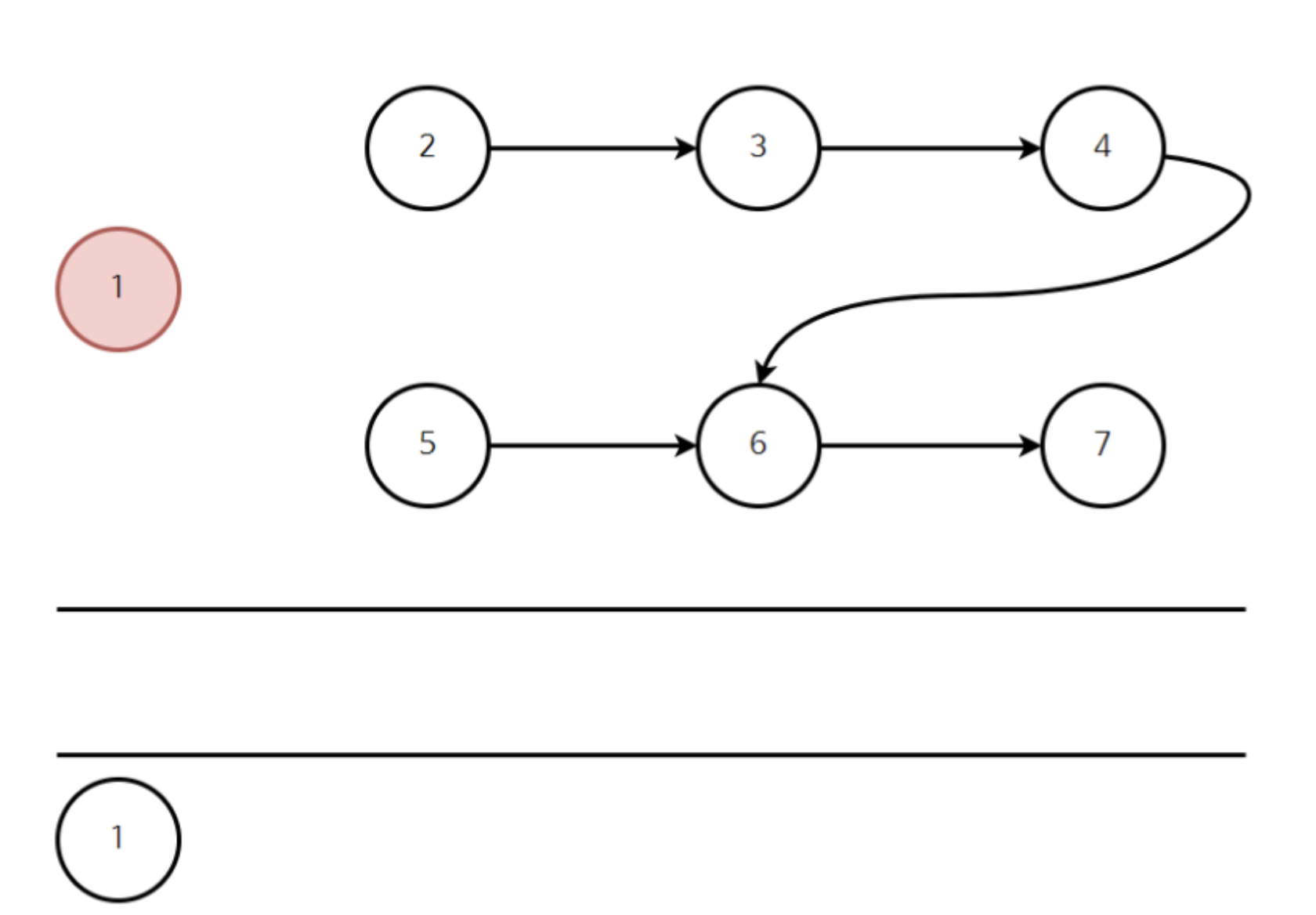
위와 같이 1을 큐에서 빼낸 뒤 정점과 연결된 간선을 끊어주었다면, 다음과 같이 진입차수 리스트가 갱신된다.

다음으로는 2와 5의 진입차수가 0이므로 큐에 넣어준다.
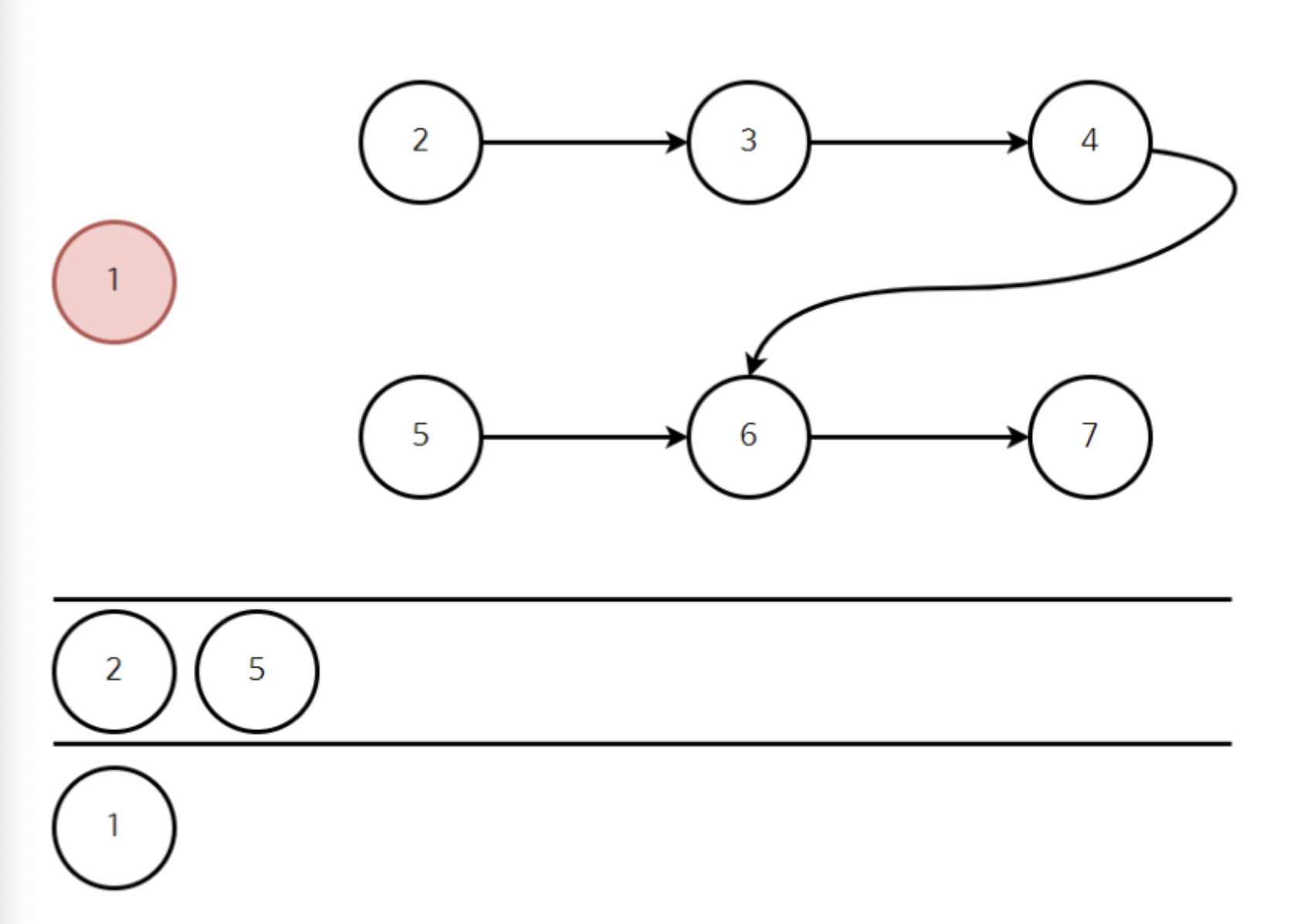
앞선 과정과 마찬가지로 2를 큐에서 빼고, 2와 연결된 간선을 끊어준다.
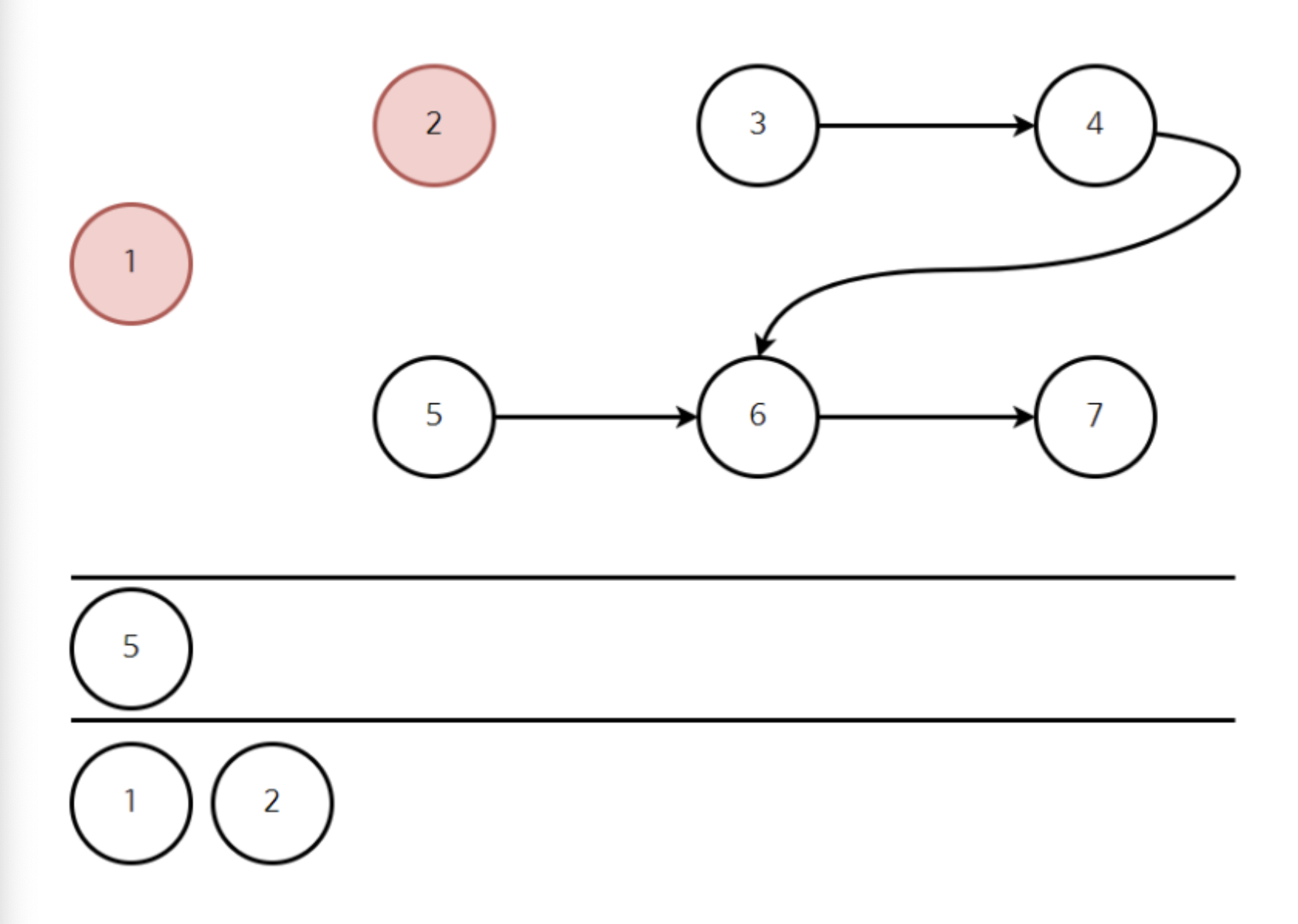
이후 진입 차수 리스트는 다음과 같이 갱신된다.

이런 과정을 반복하면 최종적으로 1 2 5 3 4 6 7 순으로 큐에서 pop 되게 되는데, 이 결과가 곧 위상 정렬의 결과가 된다.
위상 정렬의 시간복잡도는 O(V+E) V: 정점 개수, E: 간선 개수 만큼 소요되므로, 매우 빠른 알고리즘 중 하나이다.
출처

