99클럽 코테 스터디 6일차 TIL + BFS/DFS

초코소금빵·2025년 1월 20일

오늘의 문제

https://www.acmicpc.net/problem/1260

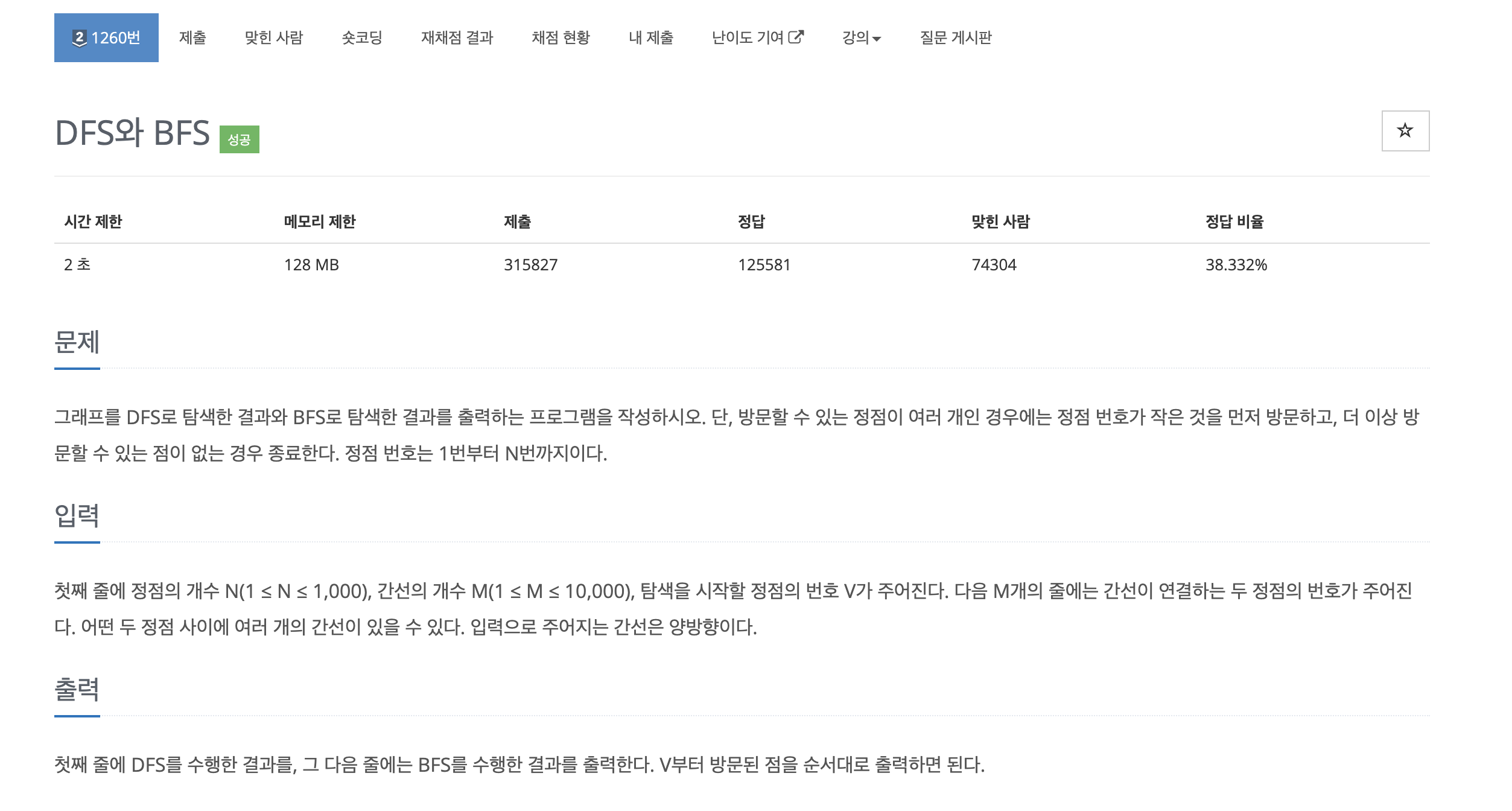
문제 이해

BFS (Breadth-First Search)
정의
BFS는 시작 노드에서 가까운 노드부터 순차적으로 탐색하는 알고리즘이다. 계층적으로 탐색하므로, 최단 경로를 찾는 데 적합하다.

작동 방식
1.시작 노드를 큐에 삽입.
2.큐에서 노드를 꺼내어 연결된 모든 인접 노드를 큐에 삽입 (방문 체크 필수).
3.큐가 빌 때까지 반복.

특징
탐색 구조: 너비 우선 (Level by Level 탐색).
자료 구조: 큐 사용.
시간 복잡도: 𝑂(𝑉+𝐸) V는 노드 수, E는 간선 수.
장점: 최단 경로 탐색 보장.
단점: 메모리 사용량이 많음 (큐를 사용하므로).

적용 예시
최단 경로 탐색 (예: 미로 탈출).
SNS 친구 추천 알고리즘 (근접 탐색).

DFS (Depth-First Search)

정의
DFS는 시작 노드에서 한 경로를 끝까지 탐색한 후, 다시 다른 경로를 탐색하는 방식이다. 재귀적 탐색을 사용하며, 백트래킹 기법과도 관련이 깊다.

작동방식
1.시작 노드를 스택에 삽입.
2.스택의 최상단 노드를 꺼내어 방문.
3.방문하지 않은 인접 노드를 스택에 삽입.
4.스택이 빌 때까지 반복 (또는 재귀적으로 탐색).

특징
탐색 구조: 깊이우선 (경로 끝까지 탐색 후 백트래킹)
자료 구조: 스택
시간 복잡도: 𝑂(𝑉+𝐸) V는 노드 수, E는 간선 수.
장점: 메모리 효율적(단순한 그래프에서)
단점: 최단 경로 보장 X

적용 예시
순열 및 조합생성
그래프 연결 요소 탐색
게임에서 경로 찾기

Python 예시 코드

BFS

from collections import deque
def bfs(graph, start):
    visited = set()
    queue = deque([start])
    visited.add(start)
	while queue:
        node = queue.popleft()
        print(node, end=' ')
        for neighbor in graph[node]:
            if neighbor not in visited:
                queue.append(neighbor)
                visited.add(neighbor)
graph = {
    1: [2, 3],
    2: [4, 5],
    3: [],
    4: [],
    5: []
}
bfs(graph, 1)

DFS

def dfs(graph, node, visited):
    if node not in visited:
        visited.add(node)
        print(node, end=' ')
        for neighbor in graph[node]:
            dfs(graph, neighbor, visited)
graph = {
    1: [2, 3],
    2: [4, 5],
    3: [],
    4: [],
    5: []
}
dfs(graph, 1, set())

문제 코드

n, M, v = map(int, input().split())
m = [[0] * (n+1) for i in range(n+1)]
#방문
visited = [0] * (n+1)
for i in range(M):
    a, b = map(int, input().split())
    m[a][b] = m[b][a] = 1
def dfs(v):
    visited[v] = 1
    print(v, end=' ')
    for i in range(1, n+1):
        if visited[i] == 0 and m[v][i] ==1:
            dfs(i)
def bfs(v):
    #방문해야할 곳을 순서대로 넣을 큐
    queue = [v]
    #dfs를 완료한 visited배열(1로 되어있음)에서 0으로 방문 체크
    visited[v] = 0
    while queue:
        v = queue.pop(0)
        print(v, end=' ')
        for i in range(1, n+1):
            if visited[i] == 1 and m[v][i] == 1:
                queue.append(i)
                visited[i] = 0