Algorithm[Java] | BFS, DFS 정리

sammy·2023년 7월 25일
BFSDFS알고리즘

Algorithm[Java]

목록 보기
1/6

그래프를 탐색하는 방법 중 BFS(넓이 우선 탐색)와 DFS(깊이 우선 탐색) 두 가지를 비교 해보겠습니다.

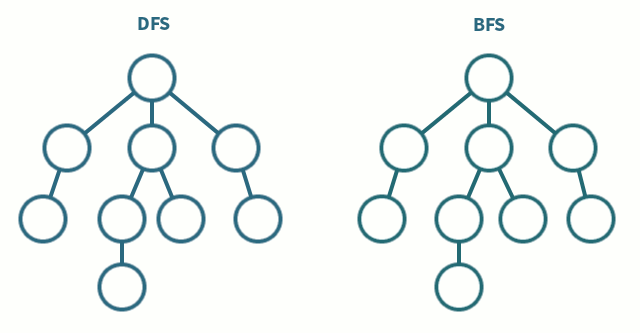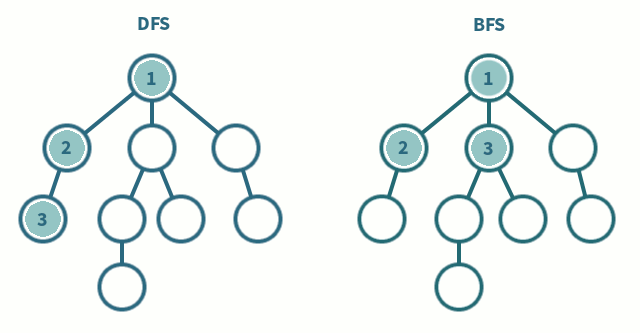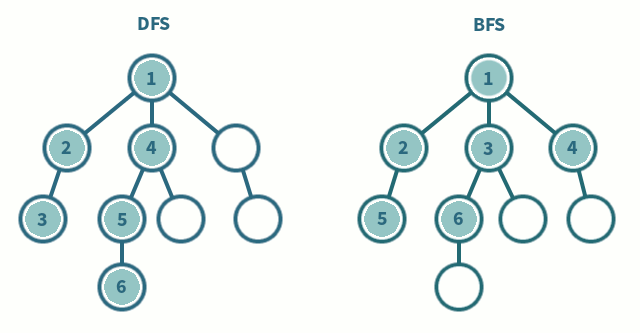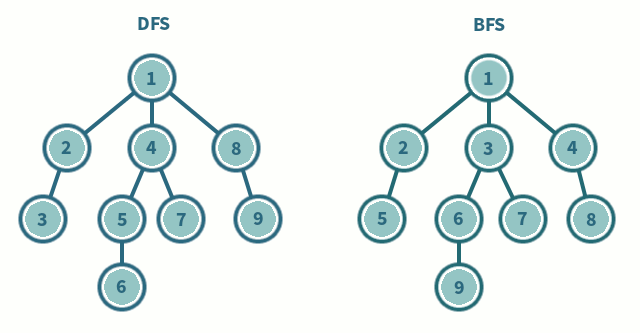
BFS - 루트를 시작으로 주변에 있는 정점들을 먼저 방문하는 방법으로 트리의 레벨 순회와 같습니다.

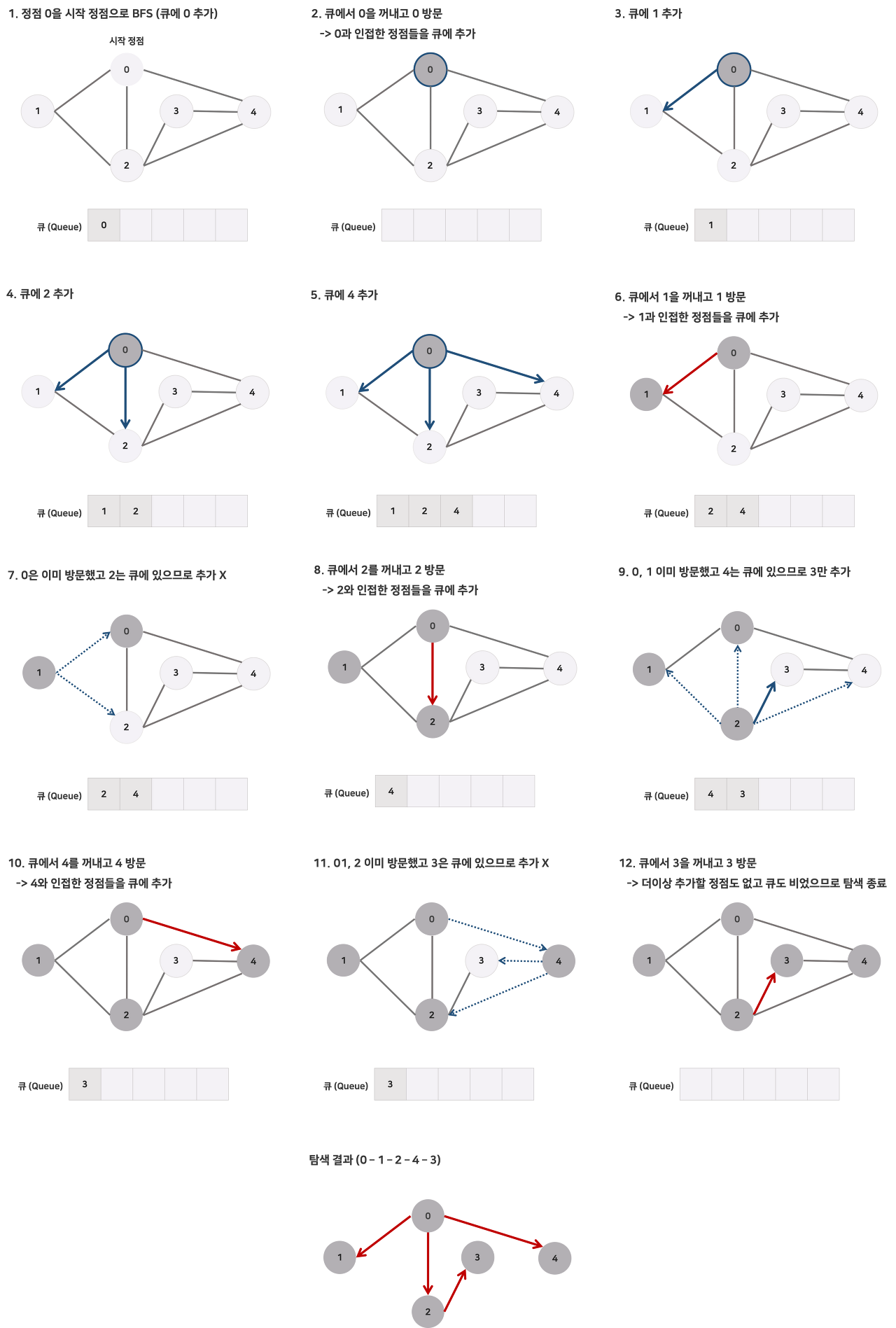
[출처] https://minhamina.tistory.com/36?category=837168

DFS - 한 번 갔던 방향으로 계속해서 정점들을 방문하는 방법으로 트리의 전위 순회와 같습니다.

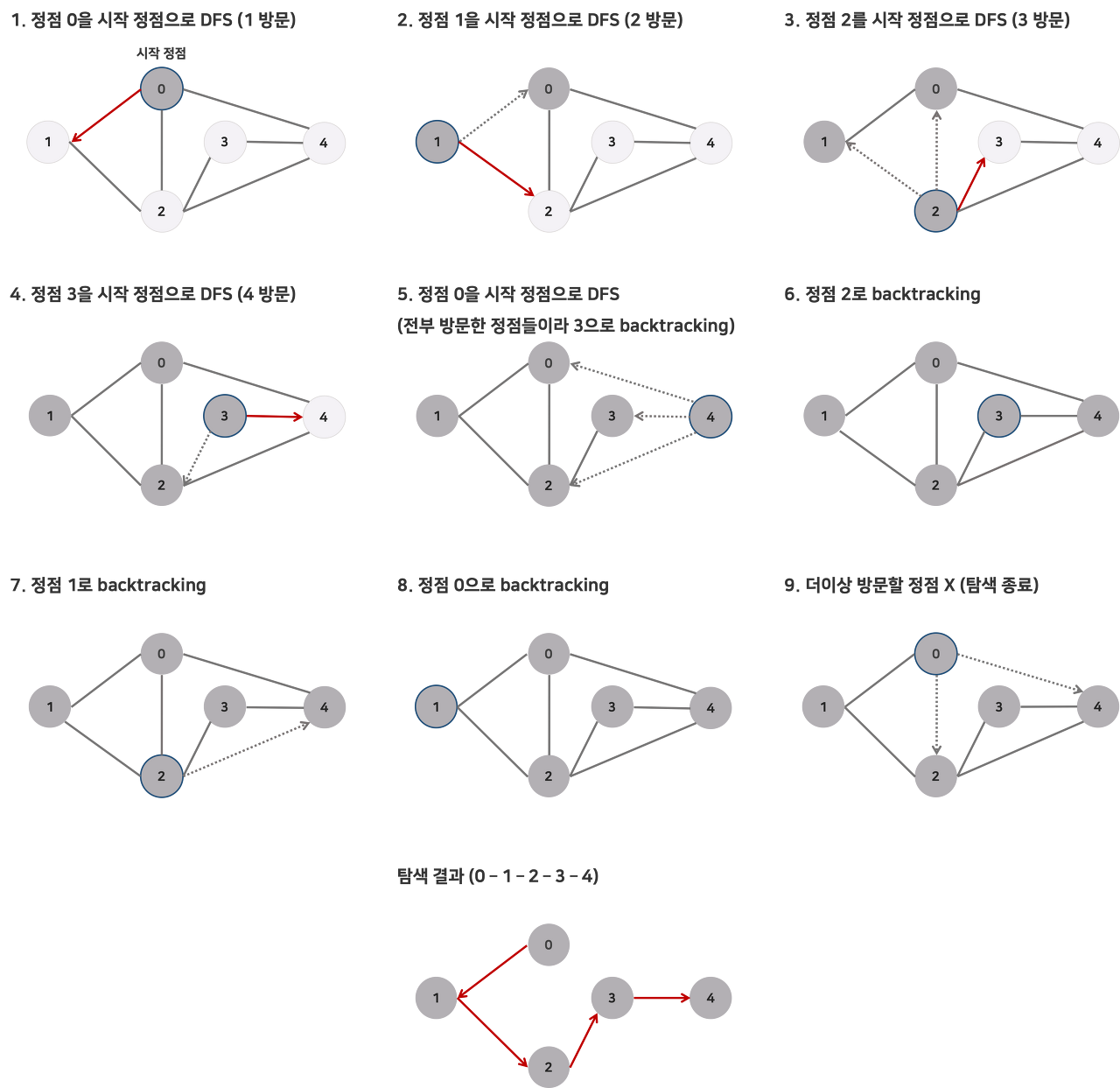
[출처] https://minhamina.tistory.com/22?category=837168

BFS 장단점

장점

  • 너비를 우선으로 탐색하므로 답이 되는 경로가 여러 개인 경우에도 최단경로를 얻을 수 있다.
  • 경로가 무한히 깊어져도 최단경로를 반드시 찾을 수 있다.
  • 노드 수가 적고 깊이가 얕은 해가 존재할 때 유리하다.

단점

  • DFS와 달리 큐를 이용하여 다음에 탐색할 정점들을 저장하기 때문에 더 큰 저장공간을 필요로 한다.
  • 노드의 수가 늘어나면 탐색해야 하는 노드가 많아지기 때문에 비효율적이다.

DFS의 장단점

장점

  • 현 경로상의 노드들만 기억하면 되기 때문에 저장공간 수요가 비교적 적다.
  • 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.

단점

  • 해가 없는 경로가 깊을 경우 탐색시간이 오래 걸릴 수 있다.
  • 얻어진 해가 최단 경로가 된다는 보장이 없다.
  • 깊이가 무한히 깊어지면 스택오버플로우가 날 위험이 있기 때문에 깊이에 제한을 줌으로써 이를 해결한다.

BFS vs DFS 정리

BFSDFS
큐로 구현한다.스택 또는 재귀 함수로 구현한다.
루트를 시작으로 주변에 있는 정점들을 먼저 방문한다.한 번 갔던 방향으로 계속해서 정점들을 방문한다.

BFS vs DFS 코드 작성법

BFS

n: 정점의 수, e: 간선의 수
인접 리스트 : 리스트로 그래프의 연결 관계를 표현하는 방식 O(n+e)
인접 행렬 : 2차원 배열로 그래프의 연결 관계를 표현하는 방식 O(n^2)

1. 인접 리스트로 BFS 구현

import java.util.*;

public class BFS_List {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		int n = sc.nextInt(); // 정점의 개수 
		int m = sc.nextInt(); // 간선의 개수 
		int v = sc.nextInt(); // 탐색을 시작할 정점의 번호 

		boolean visited[] = new boolean[n + 1]; // 방문 여부를 검사할 배열 

		LinkedList<Integer>[] adjList = new LinkedList[n + 1];

		for (int i = 0; i <= n; i++) {
			adjList[i] = new LinkedList<Integer>();
		}

		// 간선의 개수 만큼 반복, 입력으로 주어지는 간선은 양방향
		for (int i = 0; i < m; i++) {
			int v1 = sc.nextInt();
			int v2 = sc.nextInt();
			adjList[v1].add(v2);
			adjList[v2].add(v1);
		}

		for (int i = 1; i <= n; i++) { 
			Collections.sort(adjList[i]); // 방문 순서를 위해 오름차순 정렬 
		}

		System.out.println("[인접리스트 활용 BFS 큐로 구현]");
		bfs_list(v, adjList, visited);
	}

	// 인접리스트를 활용한 BFS 
	public static void bfs_list(int v, LinkedList<Integer>[] adjList, boolean[] visited) {
		Queue<Integer> queue = new LinkedList<Integer>();
		visited[v] = true; // 방문 처리
		queue.add(v); // 큐에 넣기

		while(queue.size() != 0) { 
			v = queue.poll(); 
			System.out.print(v + " ");

			Iterator<Integer> iter = adjList[v].listIterator();
			
			while(iter.hasNext()) { 
				int nextV = iter.next(); 
				if(!visited[nextV]) { 
					visited[nextV] = true; 
					queue.add(nextV); 
				} 
			}
		}
	}

}
[input]
5 5 3
5 4
5 2
1 2
3 4
3 1

[Output]
[인접리스트 활용 BFS 큐로 구현]
3 1 4 2 5

2. 인접 행렬로 BFS 구현

import java.util.*;

public class BFS_Array {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		int n = sc.nextInt(); // 정점의 개수 
		int m = sc.nextInt(); // 간선의 개수 
		int v = sc.nextInt(); // 탐색을 시작할 정점의 번호 

		boolean visited[] = new boolean[n + 1]; // 방문 여부를 검사할 배열 

		int[][] adjArray = new int[n+1][n+1];

		// 간선의 개수 만큼 반복, 입력으로 주어지는 간선은 양방향
		for(int i = 0; i < m; i++) {
			int v1 = sc.nextInt();
			int v2 = sc.nextInt();

			adjArray[v1][v2] = 1;
			adjArray[v2][v1] = 1;
		}

		System.out.println("[인접행렬 활용 BFS 큐로 구현]");
		bfs_array(v, adjArray, visited);
	}
	
	// 인접행렬을 활용한 BFS 
	public static void bfs_array(int v, int[][] adjArray, boolean[] visited) {
		Queue<Integer> q = new LinkedList<>();
		int n = adjArray.length - 1;

		q.add(v);
		visited[v] = true;

		while (!q.isEmpty()) {
			v = q.poll(); // 큐에서 하나씩 꺼냄.
			System.out.print(v + " ");

			for (int i = 1; i <= n; i++) {
				if (adjArray[v][i] == 1 && !visited[i]) {
					q.add(i);
					visited[i] = true;
				}
			}
		}
	}
	
}
[input]
5 5 3
5 4
5 2
1 2
3 4
3 1

[Output]
[인접행렬 활용 BFS 큐로 구현]
3 1 4 2 5

DFS

구현 방법 2가지

  • 재귀함수 활용
  • 스택 활용

n: 정점의 수, e: 간선의 수
인접 리스트 : 리스트로 그래프의 연결 관계를 표현하는 방식 O(n+e)
인접 행렬 : 2차원 배열로 그래프의 연결 관계를 표현하는 방식 O(n^2)

1. 인접 리스트로 DFS 구현

import java.util.*;

public class DFS_List_Recursion {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		int n = sc.nextInt(); // 정점의 개수 
		int m = sc.nextInt(); // 간선의 개수 
		int v = sc.nextInt(); // 시작 정점

		boolean visited[] = new boolean[n + 1]; // 방문 여부 확인 배열

		LinkedList<Integer>[] adjList = new LinkedList[n + 1];

		for (int i = 1; i <= n; i++) {
			adjList[i] = new LinkedList<Integer>();
		}

		// 간선의 개수 만큼 반복, 입력으로 주어지는 간선은 양방향
		for (int i = 0; i < m; i++) {
			int v1 = sc.nextInt();
			int v2 = sc.nextInt();
			adjList[v1].add(v2);
			adjList[v2].add(v1);
		}

		for (int i = 1; i <= n; i++) { // 방문 순서는 작은거 우선적으로 큐에서 뽑기 위해 오름차순 정렬 
			Collections.sort(adjList[i]);
		}

		System.out.println("[인접리스트 활용 DFS 스택으로 구현]");
		dfs_list_recursion(v, adjList, visited);
	}
	
	// 인접 리스트를 활용한 재귀문으로 구현
	public static void dfs_list_recursion(int v, LinkedList<Integer>[] adjList, boolean[] visited) {
		visited[v] = true; // 정점 방문 Check
		System.out.print(v + " "); // 정점 출력

		Iterator<Integer> iter = adjList[v].listIterator(); // 정점 인접리스트 순회
		while (iter.hasNext()) {
			int nextV = iter.next();
			if (!visited[nextV]) // 방문하지 않은 정점이라면 
				dfs_list_recursion(nextV, adjList, visited); // 다시 DFS 실행
		}
	}
}
[input]
5 5 3
5 4
5 2
1 2
3 4
3 1

[Output]
[인접리스트 활용 DFS 스택으로 구현]
3 1 2 5 4

2. 인접 행렬로 DFS 구현

import java.util.*;

public class DFS_Array {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);

		int n = sc.nextInt(); // 정점의 개수 
		int m = sc.nextInt(); // 간선의 개수 
		int v = sc.nextInt(); // 탐색을 시작할 정점의 번호 

		boolean visited[] = new boolean[n + 1]; // 방문 여부를 검사할 배열 

		int[][] adjArray = new int[n+1][n+1];

		// 간선의 개수 만큼 반복, 입력으로 주어지는 간선은 양방향
		for(int i = 0; i < m; i++) {
			int v1 = sc.nextInt();
			int v2 = sc.nextInt();

			adjArray[v1][v2] = 1;
			adjArray[v2][v1] = 1;
		}
		
        System.out.println("[인접행렬 활용 DFS 재귀로 구현]");
		dfs_array_recursion(v, adjArray, visited);
        
        // DFS 스택으로 구현하기 위해 visited 배열 초기화
		Arrays.fill(visited, false); 
		
        System.out.println("\n[인접행렬 활용 DFS 스택으로 구현]");
		dfs_array_stack(v, adjArray, visited, true);
	}
	
	// 인접 행렬을 활용한 DFS 재귀로 구현
	public static void dfs_array_recursion(int v, int[][] adjArray, boolean[] visited) {
		int l = adjArray.length-1;
		visited[v] = true;
		System.out.print(v + " ");

		for(int i = 1; i <= l; i++) {
			if(adjArray[v][i] == 1 && !visited[i]) {
				dfs_array_recursion(i, adjArray, visited);
			}
		}
	}
    
    // 인접 행렬을 활용한 DFS 스택으로 구현
	public static void dfs_array_stack(int v, int[][] adjArray, boolean[] visited, boolean flag) {
		int l = adjArray.length-1;
		Stack<Integer> stack = new Stack<Integer>();
		stack.push(v);
		visited[v] = true;
		System.out.print(v + " ");

		while(!stack.isEmpty()) {
			int w = stack.peek(); // stack의 맨 위에 있는 요소 반환
			flag = false; 

			for(int i = 1; i <= l; i++) {
				if(adjArray[w][i] == 1 && !visited[i]) {
					stack.push(i);
					System.out.print(i + " ");
					visited[i] = true;
					flag = true;	
					break;
				}
			}

			if(!flag) {
				stack.pop();
			}
		}
	}	
}
[Input]
5 5 3
5 4
5 2
1 2
3 4
3 1

[Output]
[인접행렬 활용 DFS 재귀로 구현]
3 1 2 5 4 
[인접행렬 활용 DFS 스택으로 구현]
3 1 2 5 4

[참고자료]
https://minhamina.tistory.com/36
https://minhamina.tistory.com/22

profile
sammy
누군가에게 도움을 주기 위한 개발자로 성장하고 싶습니다.
다음 포스트

Algorithm[Java] | 완전탐색 - 순열

0개의 댓글