Algorithm[Java] | 분할 정복

오늘은 분할 정복에 대해 간단히 알아보도록 하겠습니다.

💡 분할 정복 vs DP

▪️ 분할 정복은 큰 문제를 작은 부분 문제로 나눈 뒤 각 부분 문제를 독립적으로 해결하고 합치는 접근 방식으로 대표적인 예로 큰 수의 곱셈, 퀵 정렬, 병합 정렬 등이 있습니다.

▪️ 동적 계획법은 중복되는 부분 문제를 효율적으로 해결하여 최적화하는 방식으로 대표적인 예로 피보나치 수열과 배낭 문제 등..이 있습니다.

분할 정복을 예제를 통해 이해해 보도록 하겠습니다.

1. 거듭 제곱

거듭제곱을 일반 재귀문으로 짤 경우 O(n), 분할 정복 기반 재귀문으로 짤 경우 O(logN)의 시간복잡도를 갖게됩니다. 일반 재귀와 분할 정복 기반 재귀문을 그림으로 확인해보면 다음과 같습니다.

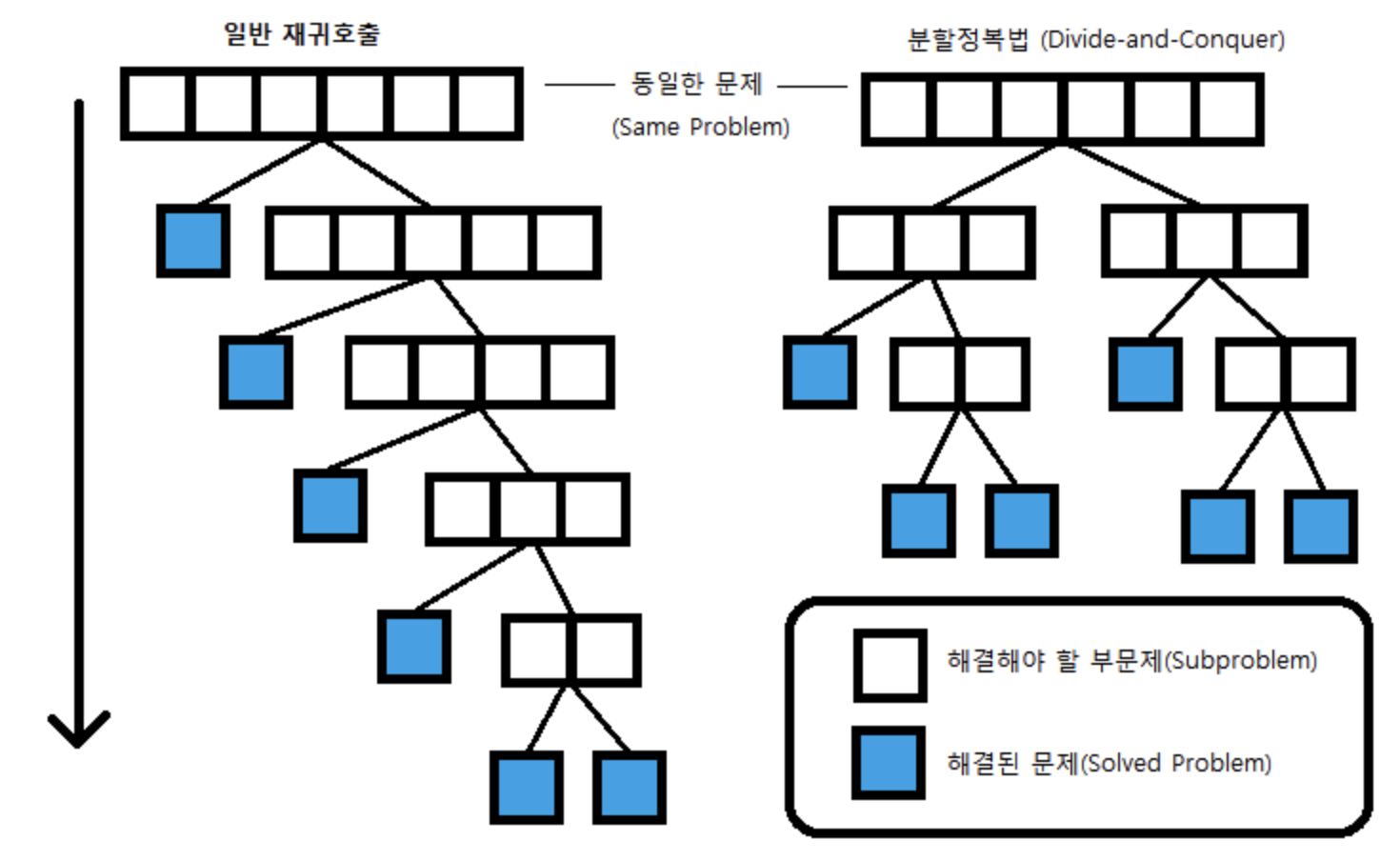[참고 이미지] https://gamedevlog.tistory.com/58

코드로 작성해보면 다음과 같습니다.

import java.util.Scanner;

public class SquareNumberTest {
	public static int normal_Recursion_cnt,divideAndConquer_Recursion_cnt;
	
	public static void main(String[] args) {
		Scanner sc =new Scanner(System.in);
		
		long X=sc.nextLong();
		int N=sc.nextInt();

		System.out.println(normal_Recursion(X,N));
		System.out.println("일반 재귀함수 : "+normal_Recursion_cnt);
		System.out.println(divideAndConquer_Recursion(X,N));
		System.out.println("분할정복 적용 재귀함수 : "+divideAndConquer_Recursion_cnt);
		
		// 스캐너 close 
		sc.close();
	}
	 
	/**
	 * 재귀 : 분할정복 미적용
	 * x^n = x * x^(n-1)
	 * x^(n-1)=x * x^(n-2)
	 * 
	 */
	
	public static long normal_Recursion(long x,int n) {
		normal_Recursion_cnt++; // 재귀 호출 횟수 
		
		if(n==1) return x; // 기저조건 
		return x*normal_Recursion(x,n-1);
	}

	/**
	 * 재귀 : 분할 정복 적용 함수 
	 * n: 짝수 x^n = x^(n/2) * x^(n/2)
	 * n: 홀수 x^n =x * x^(n/2) * x^(n/2)
	 * 
	 */

	public static long divideAndConquer_Recursion(long x, int n) {
		divideAndConquer_Recursion_cnt++; // 재귀 호출 횟수
		
		if(n==1) return x; // 기저조건
		long y = divideAndConquer_Recursion(x,n/2);
		return (n%2==0) ? y*y: y*y*x;
	}
}

2. 백준 1992번 쿼드트리 문제

https://www.acmicpc.net/problem/1992

쿼드트리는 대표적인 분할정복 문제입니다. 이 문제를 풀어보면 다음과 같습니다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;

/**
 * [문제 이해] 
 * 영상의 크기 N
 * 주어진 영상이 모두 0으로만 되어 있으면 압축 결과는 "0"
 * 모두 1로만 되어 있으면 압축 결과는 "1"
 * 만약 0과 1이 섞여 있으면 전체를 한 번에 나타내지를 못하고,왼쪽 위, 오른쪽 위, 왼쪽 아래, 오른쪽 아래, 이렇게 4개의 영상으로 나누어 압축
 * 
 * [입력]
 * N
 * 
 * [출력]
 * 영상 앞축 결과
 * 
 * [문제해결 프로세스]
 * 분할정복을 이용하자
 * 1. 합으로 모두 0인지 1인지 판단한다. sum=0 -> 0, sum=size*size -> 1
 * 1-1. 영상이 모두 0으로 되어있으면 0
 * 1-2. 영상이 모두 1로 되어있으면 1
 * 2. 만약 영상이 0,1이 섞여있다면 4분할 하기 (재귀호출) 이때 괄호를 열고, 재귀가 끝나면 괄호 닫기
 *
 */

public class Main_BJ_1992_쿼드트리_안성재 {
	public static int N,arr[][];
	public static StringBuilder sb = new StringBuilder();
	
	public static void main(String[] args) throws NumberFormatException, IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		N = Integer.parseInt(br.readLine());
		arr = new int[N][N]; // 배열 초기화
		
		for(int r=0;r<N;r++) {
			String[] row = br.readLine().split("");
			for(int c=0;c<N;c++) {
				arr[r][c]=Integer.parseInt(row[c]);
			}
		}
		
		solution(0, 0, N);
		System.out.println(sb);
	}
	
	public static void solution(int sr,int sc,int size) {
		int sum=0;
		
		for(int r=sr;r<sr+size;r++) {
			for(int c=sc;c<sc+size;c++) {
				sum+=arr[r][c];
			}
		}
		
		
		if(sum == (size*size) || sum == 0) { // 더이상 안나눠도 된다면
			sb.append(sum / (size*size));
			return;
		}else {
			int half = size/2;
			sb.append("(");
			solution(sr, sc, half);
			
			solution(sr, sc+half, half);

			solution(sr+half, sc, half);
			
			solution(sr+half, sc+half, half);
			sb.append(")");
		}
	}

}

3. 이진 탐색(Binary Search)

이진 탐색 또한 분할 정복을 활용한 알고리즘입니다.

💡 이진 탐색 고려사항
▪️ N이 큰가?
▪️ 정렬이 가능한가?

💡 이진 탐색 과정
1. 자료의 중아에 있는 원소 선택.
2. 중앙 원소의 값(mid)과 찾고자 하는 목표 값(target) 비교.
3-1. 중앙 원소의 값(mid)과 찾고자 하는 목표 값(target)이 일치한다면 탐색 종료.
3-2. 목표 값(target)이 중앙 원소의 값(mid)보다 작으면 왼쪽 절반, 크면 오른쪽 절반에 대해 새로 탐색 수행. (찾을 때까지)

💡 이진 탐색 구현 방법
1.반복문을 통한 구현

public static boolean BSearch(int[] arr, int n) {
		int left = 0;
		int right = arr.length - 1;
		int mid;

		while (left <= right) {
			mid = (left + right) / 2;
			if (arr[mid] < n) left = mid + 1;
			else if (arr[mid] > n) right = mid - 1;
			else return true;
		}
		return false;
	}

2. 재귀로 구현

public static boolean RecursiveBSearch(int[] arr, int n, int left, int right) {
		if(left > right) return false;
		
		int mid = (left + right) / 2;
        
		if (arr[mid] < n) 
        	return RecursiveBSearch(arr, n, mid +1, right);
		else if (arr[mid] > n) 
        	return RecursiveBSearch(arr, n, left, mid - 1);
		else 
        	return true;
	}