탐색이란 많은 양의 데이터중에서 원하는 데이터를 찾는 과정.
대표적인 그래프 탐색 알고리즘으론 DFS / BFS가 있음.
stack 자료구조
- FILO 형식(선입 후출)의 자료구조.
let stack =[];
stack.push(1);
stack.push(2);
stack.push(3);
stack.push(4);
stack.push(5);
stack.push(6);
stack.pop();
stack.push(1);
stack.push(2);
stack.pop();
console.log(stack);
let reserve=stack.slice().reverse();
console.log(reserve); //최상단 원소부터 출력 이부분은 [...stack].reverse()로도 할 수 있음.(불변성을 지키기위해 slice()를 사용했기에 스프레드문법으로도 가능)
console.log(stack);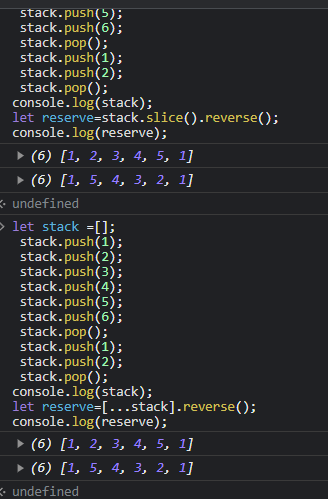
- 재귀적인 방법으로 구현
const graph = {
A: ['B', 'C'],
B: ['A', 'D', 'E'],
C: ['A', 'F', 'G'],
D: ['B'],
E: ['B'],
F: ['C'],
G: ['C'],
};
const visited = new Set();
function dfsRecursive(node) {
// 현재 노드를 방문 처리
visited.add(node);
// 현재 노드를 출력하거나 원하는 작업 수행
console.log(node);
// 현재 노드와 인접한 노드들을 순회
for (const neighbor of graph[node]) {
// 방문하지 않은 노드라면 재귀적으로 DFS 호출
if (!visited.has(neighbor)) {
dfsRecursive(neighbor);
}
}
}
// 시작 노드를 'A'로 설정하여 DFS 호출
dfsRecursive('A');
2.stack 으로 dfs구현
const graph = {
A: ['B', 'C'],
B: ['A', 'D', 'E'],
C: ['A', 'F', 'G'],
D: ['B'],
E: ['B'],
F: ['C'],
G: ['C'],
};
const visited = new Set();
function dfsIterative(startNode) {
// 스택을 생성하고 시작 노드를 스택에 넣음
const stack = [startNode];
// 스택이 빌 때까지 반복
while (stack.length > 0) {
// 스택의 가장 위에 있는 노드를 꺼냄
const node = stack.pop();
// 해당 노드가 방문되지 않았을 경우에만 수행
if (!visited.has(node)) {
// 현재 노드를 방문 처리
visited.add(node);
// 현재 노드를 출력하거나 원하는 작업 수행
console.log(node);
// 현재 노드와 인접한 노드들을 순회
for (const neighbor of graph[node]) {
// 방문하지 않은 노드라면 스택에 추가
if (!visited.has(neighbor)) {
stack.push(neighbor);
}
}
}
}
}
// 시작 노드를 'A'로 설정하여 DFS 호출
dfsIterative('A');
