알고리즘의 성능 분석

실행시간 측정 방법

알고리즘 간 성능분석을 함에 있어서 가장 간단하고 편리한 방법은 두 프로그램을 실제로 컴퓨터에서 돌려보는 방법입니다. 다만 이 방법은 입력되는 자료의 개수 등 특정 조건에 따라 영향을 받을 수 있기 때문에 측정 시마다 효율적인 것으로 기대되는 알고리즘이 달라질 수 있습니다. 이를 보완하기 위해 나온 개념이 알고리즘의 복잡도(complexity) 개념입니다.

알고리즘의 복잡도 분석

이 방법은 구현하지 않고도 모든 입력을 고려하는 방법입니다. 하드웨어나 소프트웨어 환경과 관계 없이 알고리즘의 효율성을 분석할 수 있다는 장점이 있습니다. 복잡도는 크게 걸리는 시간을 나타내는 시간복잡도와 쓰이는 메모리의 용량을 나타내는 공간복잡도로 나뉩니다. 그러나 대부분의 사용자는 프로그램이 메모리를 얼마나 사용하는지보다 결과가 얼마나 더 빨리 도출되는지에 관심이 있기 때문에, 시간복잡도에 대해서 말해보도록 하겠습니다.

입력되는 정수를 n이라 하고 그에 따른 시간복잡도 함수를 T(n)이라 할 때, n * n을 계산하는 두 알고리즘을 생각해봅시다.

두 알고리즘의 시간복잡도 함수를 구하는 과정은 아래와 같습니다.(단, 루프제어 연산은 생각하지 않겠습니다. 실제로도 루프제어연산이 전체 시간복잡도에 미치는 영향은 미미합니다.)

위 결과에서 나온 T(n)을 비교해보면 알고리즘 A가 알고리즘 B에 비해 더 효율적이라 판단할 수 있습니다.(물론 직관적으로도 슈도코드만 봐도 알 수 있습니다)

빅 오 $O$ 표기법

n의 크기가 커지면 커질수록 시간복잡도 함수는 최고차항에 점근하는 성질을 가지고 있습니다. 즉 일반적인 상황에서는 최고차항만 보면 알고리즘의 효율성을 어느정도 판단할 수 있다는 것을 의미합니다. 이를 수식으로 나타내기 위해 빅 오 표기법(Big-O notation)을 도입하였습니다. 빅 오 표기법의 수학적 정의는 다음과 같습니다.

두 개의 함수 $f(n), g(n)$이 주어졌을 때 모든 $n \ge n$0에 대해 $|f(n)|\le c|g(n)|$을 만족하는 상수 c와 n0가 존재하면 $f(n) = O(g(n))$이다.

이를 이해하기 쉽게 그래프로 나타내면 다음과 같습니다.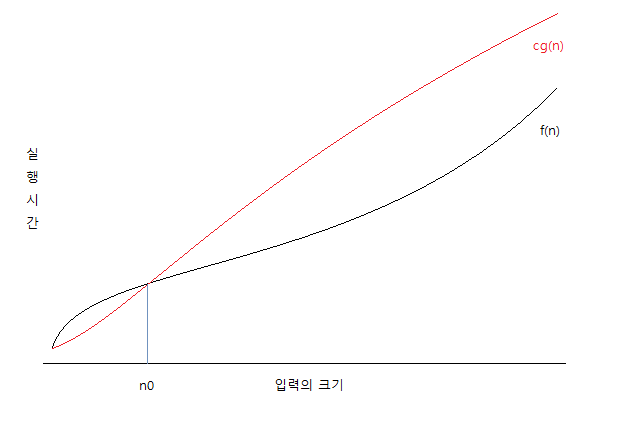

빅 오 표기법은 알고리즘의 효율성을 판단할 때 유용하게 쓰일 수 있습니다. 다음은 자주 사용되는 빅 오 표기법들로 나타낸 알고리즘들의 실행 시간을 비교한 것입니다.

$O(1)<O(logn)<O(n)<O(nlogn)<O($n2$)<O($n3$)<O(2$n$)<O(n!)$

따라서 우리는 알고리즘의 시간복잡도를 빅 오 표기법으로 나타냈을 때 O(1)를 갖는 알고리즘이 O(n)을 갖는 알고리즘보다 효율적이라고 할 수 있습니다.

그러나 빅 오 표기법은 $f(n) = 2n+1$이라고 할 때 $f(n)=O(n)$일 뿐만 아니라 $f(n)=O(n$2$)$라고도 표기할 수 있다는 한계가 있습니다. 이를 보완하기 위해 나온 표기법이 빅 오메가 표기법과 빅 세타 표기법입니다.

빅 오메가 $\Omega$ 표기법과 빅 세타 $\Theta$ 표기법

빅 오메가 표기법은 빅 오 표기법과 다르게 f(n)의 하한을 의미한다고 생각할 수 있습니다.

두 개의 함수 $f(n), g(n)$이 주어졌을 때 모든 $n \ge n$0에 대해 $|f(n)|\ge c'|g(n)|$을 만족하는 상수 c'와 n0가 존재하면 $f(n) = \Omega(g(n))$이다.

한편 빅 세타 표기법은 빅 오메가 표기법과 빅 오 표기법을 둘 다 만족할 때를 나타냅니다.

두 개의 함수 $f(n), g(n)$이 주어졌을 때 모든 $n \ge n$0에 대해 $c|g(n)|\ge|f(n)|\ge c'|g(n)|$을 만족하는 상수 c와 c', n0가 존재하면 $f(n) = \Theta(g(n))$이다.

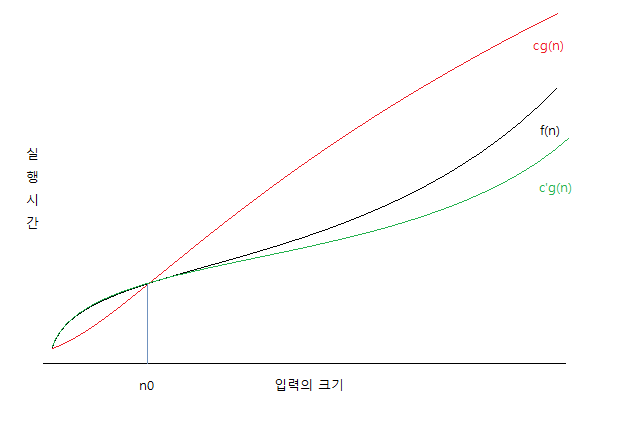
세 표기법 중에 알고리즘의 효율성을 판단함에 있어 가장 정확한 것은 빅 세타 표기법입니다. 그러나 통상적으로 빅 오 표기법을 자주 사용하며, 이때 최소 차수로 상한을 표시한다고 가정합니다.

---

벨로그에서 <sup>과 <sub>으로 위첨자하고 아래첨자가 나타나질 않는군요 ㅠㅠ
에디터에서는 보이는데....
해결 방법 아시는 분 댓글로 알려주시면 감사하겠습니다 ㅎㅎ