1. 동적계획법

주어진 문제의 해를 부분문제들의 해를 이용해 구한다. 분할과 정복과 달리 부분문제들이 서로 독립적이지 않다

• 주로 최적화 문제(목적함수 값을 최대 or 최소로 하는 해를 구하는 문제) 해결에 사용한다

동적계획법을 이용한 문제 해결을 4단계를 거친다
1) 최적해의 구조를 파악
2) 최적해의 값을 재귀적으로 정의
3) 재귀적 정의로부터 최적해의 값을 buttom-up 혹은 top-down으로 구하며 테이블에 저장
4) 테이블을 이용해 최적해 탐색

1-1. Memoization (Top-down)

• 재귀를 통해 부분문제를 풀고, 부분문제 해를 저장한다. 이후 동일 부분문제가 나올시 저장된 데이터를 확인한다

1-2. Bottom-Up

• 작은 부분문제부터 시작해 큰 부분문제까지 저장하며 해를 구한다. 문제 해를 구할때 다시 계산하지 않고 저장된 데이터를 확인한다

---

2. 피보나치 수열

• 점화식

f(0) = 0
f(1) = 1
f(n) = f(n-1) + f(n-2)

• 이를 분할과 정복으로 풀면 동일한 부분문제 해를 여러번 구해 비효율적이다
• 시간복잡도 : O(Φ^n), 대략 O(2^n)

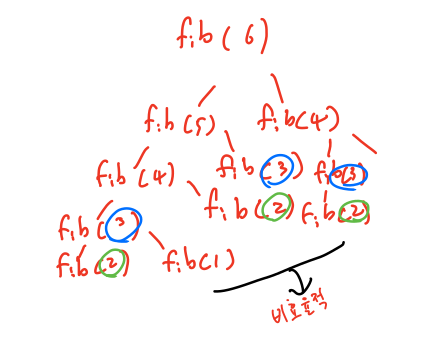
2-1. 동적계획법 Top-down

def initialize(n):
    table = [-1] * (n+1)
    table[0], table[1] = 0, 1
    return table

def fibo(n, table):
    if table[n] != -1:
        return table[n]
    table[n] = fibo(n-1, table) + fibo(n-2, table)
    return table[n]

• 시간복잡도 : O(n) = 피보나치 테이블 구성 시간복잡도

2-2. 동적계획법 Bottom-up

def fib(n):
    table = [-1] * (n+1)
    table[0], table[1] = 0, 1
    for i in range(2, n+1):
        table[i] = table[i-1] + table[i-2]
        
    return table[n]

• 시간복잡도 : O(n)

2-3. O(1) 메모리 공간 사용

fib(n)을 구하려면 fib(n-1)과 fib(n-2)만 있으면 되기 때문에 아래 알고리즘으로 공간 효율성을 높일 수 있다

def fib(n):
    if n < 2:
        return n
    
    prev_prev, prev = 0, 1
    for i in range(2, n+1):
        current = prev_prev + prev
        prev_prev = prev
        prev = current
        
    return current

---

3. 이항계수

n개의 원소에서 k개를 선택하는 경우의 수

• 점화식

nCk = 1                        if k=0 or k = n
    // n을 선택하는 경우 + n을 선택하지 않는 경우 
    = (n-1)C(k-1) + (n-1)C(k)  if 0 < k < n

• 마찬가지로 분할과 정복으로 풀시 비효율적이다
• 시간복잡도 : O(nCk)

3-1. 동적계획법

def binomial(n,k):
    table = [[0 for _ in range(n+1)] for _ in range(n+1)]
    for i in range(n+1):
        for j in range(i+1):
            if j == 0 or j == i:  # 안고르거나 모두 고르는 경우
                table[i][j] = 1
            else:
                # nCk = n-1Ck-1 + n-1Ck
                table[i][j] = table[i-1][j-1] + table[i-1][j]
    return table[n][k]

시간복잡도 : O(nk)

---

4. 동적계획법 합의 표현 문제들

4-1. 계단 문제

• 계단을 오를 때, 한번에 한 개 혹은 두개의 계단씩 오를 수 있다. n개 계단 아래에서 계단 꼭대기까지 올라가는 방법의 수를 구하시오

--> n을 1과 2의 합으로 나타낸 경우의 수를 구하는 문제

점화식

f(n) = 1                if n < 2
     // (+1로 끝나는 경우의 수) + (+2로 끝나는 경우의 수) 
     = f(n-1) + f(n-2)  if n >= 2

알고리즘

def count(n):
    table = [0] * (n+1)
    table[0] = 1
    table[1] = 1
    for i in range(2, n+1):
        table[i] = table[i-1] + table[i-2]
    return table[n]

시간복잡도 : O(n)

4-2. n의 합 표현 방법

• 양의 정수 n을 1, 3, 4의 합으로 나타내는 방법의 수를 구하시오 (1, 3, 4 사용 횟수에 제한은 없고 합에 나타나는 숫자들의 순서를 고려한다
• 예: n=6경우 6가지가 있다
  1+1+1+1+1
  1+1+3
  1+3+1
  3+1+1
  1+4
  4+1

점화식

f(n) = 1                         if n < 3
     // (+1로 끝 경우) + (+3로 끝 경우) + (+4로 끝 경우)
     = f(n-1) + f(n-3) + f(n-4)  if n >= 3

알고리즘

def count(n):
    table = [0] * (n+1)
    table[0] = table[1] = table[2] = 0
    table[3] = 2
    for i in range(4, n+1):
        table[i] = table[i-1] + table[i-3] + table[i-4]
    return table[n]

시간복잡도 : O(n)

4-3. n의 합 표현 방법 2

• 양의 정수 n을 n1 < n2 < ... < nk 의 합으로 나타내는 방법의 수를 구하시오. 숫자 횟수에 제한은 없고 합에 나타나는 숫자들의 순서를 고려한다
• 예 n = 5, n1 = 1, n2 = 3, n3 = 4
  1+1+1+1+1
  1+1+3
  1+3+1
  3+1+1
  1+4
  4+1

점화식

f(n) = 1                                  if n = 0
     = 0                                  if n < n1
     // (+n1으로 끝날 경우) + (+n2로 ... + (+nk로 끝날 경우)
     = f(n-n1) + f(n-n2) + ... + f(n-nk)  if n1 <= n

알고리즘

def count(n, numList):
    C = [0] * (n+1)
    C[0] = 1
    for i in range(numList[0], n+1)
        for x in numList:
    	    if i >= x:
    	        C[i] += C[i-x]
    	    else:
    	        break
    return C[n]	

수행시간 : O(nk)

4-4. n의 합 표현 방법 3

• 양의 정수 n에 대하여 n을 1부터 n까지 숫자의 합으로 나타내는 방법의 수를 구하시오

• 예) n=4인 경우 8가지

  1+1+1+1 2+1+1 1+2+1 3+1

  1+1+2 2+2

  1+3

  4

점화식

f(n) = 1                             if n < 2
     = f(n-1) + f(n-2) + ... f(n-n)  if n >= 2

알고리즘

def count(n):
	C = [0] * (n+1)
	C[0] = 1
	for i in range(1, n+1):
	    for j in range(i):
	    	C[i] += C[j]
	    	
	return C[n]

시간복잡도 : O(n^2)

4-5. n의 합 표현 방법 4

• 양의 정수 n에 대하여 n을 1부터 k까지 숫자들의 합으로 나타내는 방법의 수를 구하시오

점화식

f(n, k) = 1                              if n = 0 or k = 1
        = f(n-1) + f(n-2) + ... + f(n-k) if n > 0

알고리즘

def count(n, k):
    C = [0] * (n+1)
    C[0] = 1
    for i in range(1, n+1):
        for j in range(1, k+1):
            C[i] += C[j]
            
    return C[n]

시간복잡도 : O(nk)

4-6. 계단문제 2

• 계단을 오를 때, 한번에 1, 3, 4개 계단씩 오를 수 있으며, 각 계단을 밟을 때 비용이 있다. n개 계단 아래에서 계단 꼭대기까지 올라갈 때 밟는 계단의 총 비용의 최소값을 구하시오.
• 예) 6개 계단의 각 계단 비용 cost=(2,5,13,10,6,3). 최소비용 10

점화식

// f(n) : n번째 계단까지 올라갈 때 최소 비용
f(n, cost) = 0 if n = 0
     = f(n-1) + cost[n]                       if 1 <= n <= 2
     = cost[n]                                if 3 <= n <= 4
     = min{f(n-1), f(n-3), f(n-4)} + cost[n]  if n > 4

알고리즘

def countCost(n, cost):
    C = [0 for _ in range(n+1)]
    for i in range(1, n+1):
        if i == 1 or i == 2: C[i] = countCost(n-1, cost) + cost[n-1]
        elif i == 3 or i == 4: C[i] = cost[n-1]
        else:
        C[n] = min(countCost(n-1, cost), 
                   countCost(n-3, cost), 
                   countCost(n-4, cost)) + cost[n-1]
    return C[n]

시간복잡도 : O(n)

4-7. n의 합 표현 방법 5

• 양의 정수 n에 대하여 n을 1부터 n까지 숫자들의 합으로 나타내는 방법의 수를 구하시오. 단 나열되는 숫자들의 순서는 고려하지 않는다. (1+2은 2+1과 동일한 것으로 간주)

• 예) n=4 일때

1+1+1+1

1+1+2

2+2

1+3

4

점화식

f(i,j) = 1                    if i = 0
       = 1                    if j = 1
       = f(i,i)               if i < j
       // j를 사용하는 경우 + 사용하지 않는 경우
       // j를 사용할 경우 j외에 더할 수 있는 가장 큰 수는 i-j이다
       // j를 사용하지 않을 경우 1~j-1 까지로 i를 만든다
       = f(i-j,j) + f(i,j-1)  if i >= j

알고리즘

def count(n, k):
    C = [[0 for j in range(n+1)] for i in range(n+1)]
    for i in range(n+1):
        for j in range(n+1):
            if j == 1:
                C[i][j] = 1
            elif i == 0:
                C[i][j] = 1
            elif i < j:
                C[i][j] = C[i][i]
            else:
                C[i][j] = C[i-j][j] + C[i][j-1]
                
    return C[n][n]

시간복잡도 : O(n^2)

4-8 n의 합 표현 방법 6

• 양의 정수 n에 대하여 n을 1부터 k까지 숫자들의 합으로 나타내는 방법의 수를 구하시오. 단 나열되는 숫자들의 순서는 고려하지 않는다

점화식

f(n,k) = 1                    if n = 0
       = 1                    if k = 1
       = f(n,n)               if n < k
       = f(i-j,j) + f(i, j-1) if n >= k

알고리즘

def count(n, k):
    C = [[0 for j in range(n+1)] for i in range(n+1)]
    for i in range(n+1):
        for j in range(n+1):
            if j == 1:
                C[i][j] = 1
            elif i == 0:
                C[i][j] = 1
            elif i < j:
                C[i][j] = C[i][i]
            else:
                C[i][j] = C[i-j][j] + C[i][j-1]
                
    return C[n][k]

시간복잡도 : O(n^2)

4-9. 거스름돈을 주는 방법

• 돈전들의 단위 c1, c2, ... , cn이 있다. 이들 동전들을 이용하여 거스름돈 M을 나눠주는 방법의 수를 구하시오. 단 순서는 고려하지 않는다
• 예) n=3 이고 c1, c2, c3 = 1, 3, 5, M = 10일때 경우의 수는 7가지이다

점화식

// n = 동전 종류 수
f(M,n) = 0                    if n = 0
       = 1                    if n > 0 and M = 0
       = 0                    if n = 1 and M < c1
       = f(M,n-1)             if M < cn
       = f(M-cn,n) + f(M,n-1)

알고리즘

def change(M, n):
    arr = [[0 for j in range(n+1)] for i in range(M+1)]
    for i in range(M+1):
        for j in range(n+1):
            if j > 0 and i == 0:
                arr[i][j] = 1
            elif j == 1 and i < c[0]:
                arr[i][j] = 0
            elif i  <  c[j-1]:
                arr[i][j] = arr[i][j-1]
            else:
                arr[i][j] = arr[i - c[j-1]][j] + arr[i][j-1]
                
    return arr[M][n]

시간복잡도 : O(Mn)