1. 화일 조직의 기본 방법
1-1. 순차 방법
-
레코드의 논리적 순서 == 저장 순서
-
엔트리 순차 화일 : 입력 순서로 저장
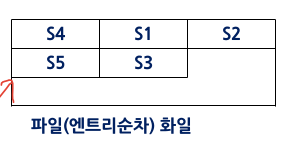
- 키 순차 파일 : 정렬되어 저장
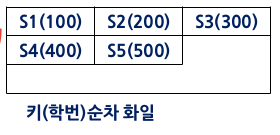
- 파일 복사, 순차적 일관 처리 응용
1-2. 인덱스 방법
- 인덱스된 순차 화일 : B+tree 사용
순차 데이터 화일 정렬x, 인덱스 화일이 키 값으로 정렬

- 다중키 화일
역 화일 : 하나의 데이터 화일에 여러 애트리뷰트 인덱스

다중 리스트 화일 : 키 값을 가지는 여러 레코드가 있음

1-3. 해싱 방법
-
다른 레코드 참조 없이 목표 레코드 접근 직접 지원 = 직접 화일
-
키 값과 레코드 주소 사이 사상 관계를 함수로 설정
-
해싱 함수 : 키 값으로부터 레코드 주소 계산
2. 인덱스
2-1. 인덱스의 종류
- 기본 vs. 보조 : 기본키의 인덱스 인가?
- 집중 vs. 비집중 : 레코드가 키 값 순으로 정렬되어 있는가? (실제 DB는 B+tree로 정렬)
- 밀집 vs. 희소 : 모든 키에 대해 인덱스 엔트리가 있는가? (각 블럭마다 한 엔트리면 희소)
- 인덱스 엔트리 = <레코드 키 값, 포인터>
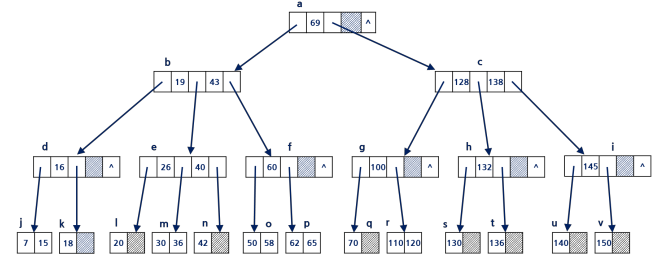
3. B-트리 인덱스
균형을 유지한 m-원 탐색 트리
- 하나의 노드 = 하나의 페이지
- 조건
i. 비었거나 높이가 1이상인 균형 m-원 탐색 트리
ii. 루트와 리프를 제외한 내부 노드는 반 이상(m/2-1) 차있음 (최소 m/2개 서브트리를 가짐)
iii. 루트는 리프가 아닌 이상 적어도 2개의 서브트리를 가짐
iv. 모든 리프는 같은 높이에 있음
3-1. B-트리 연산의 특징
-
연산의 종류 : CRUD
-
중위 순회 시 키 순서로 탐색
-
어떤 연산을 해도 균형 유지
-
삽입 연산 : 노드 오버플로우 시 재귀적 분할, 루트 분할 시 깊이 증가
-
삭제 연산 : 노드 언더플로우 시 재귀적 합병, 루트 자식이 병합되면 깊이 감소
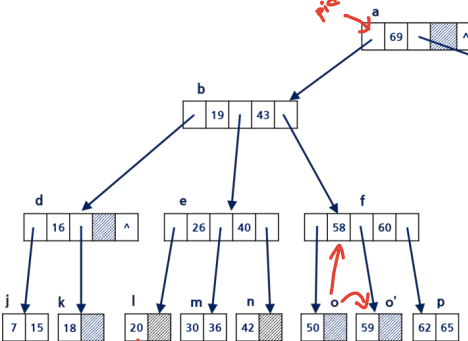
3-2. B-트리 삽입 예
-
삽입은 항상 리프 노드에서 수행
-
오버플로우 발생 시 m/2번째 키 부모 노드에 삽입 나머지 두 노드로 분할 또는 재분배
59 삽입

3-3. B-트리 삭제 예
-
리프 노드에서는 바로 삭제
-
삭제할 키가 리프가 아닌 노드에 있는 경우 항상 리프에 있는 후행 키 값과 자리 교환 후 리프에서 삭제
-
언더플로우 발생 시 절반 이상 키를 가지고 있는 형제 노드 존재 시 재분배, 불가능 시 합병
60 삭제
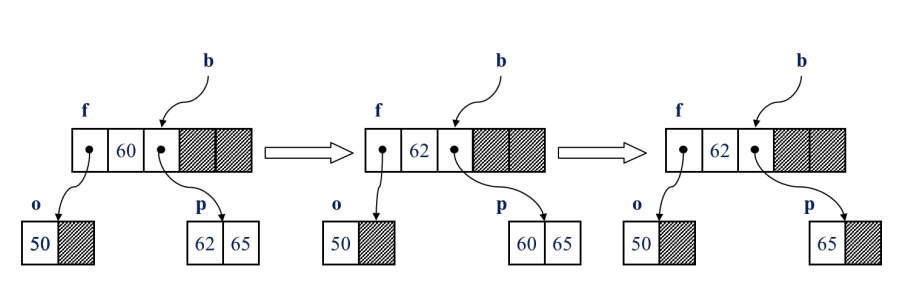
20 삭제 (재분배)
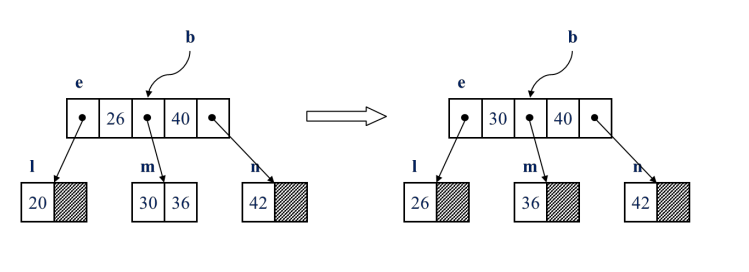
3-4. DB에서 B-트리를 사용하지 않는 이유
Range 쿼리 시
1. 중위 순회로 탐색하기 때문에 버퍼 활용도가 떨어지고 과도안 디스크 I/O가 발생한다
2. 동시 수정 시 교착 상태 방지를 위해 락을 거는데 중위 순회로 여러 트랙젝션 동시 수행이 불가하다
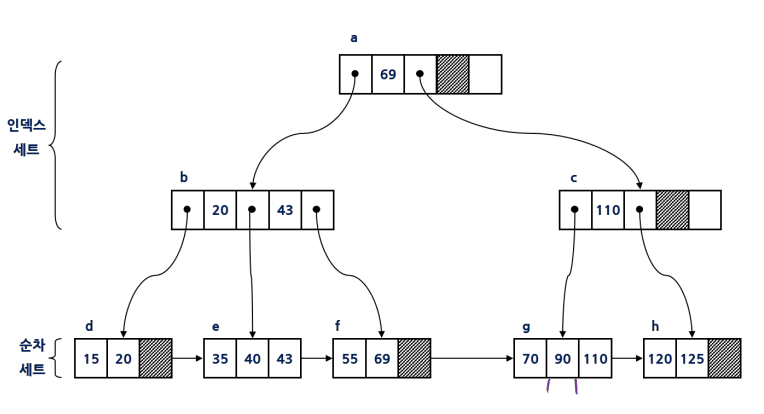
4. B+ 트리 인덱스
- 인덱스 세트 + 순차 세트
인덱스 세트 : 내부 노드, 리프 노드로 가능 경로만 제공
순차 세트 : 리프노드, 모든 키 값 저장, 순차적으로 연결
4-1. B+ 트리의 연산
-
탐색 : 인덱스 세트는 탐색 트리와 같으나 레코드는 리프에서 검색
-
삽입 : B-트리와 유사, 분할 시 중간 키 값이 분할 노드에도 존재. 리스트 순차성 유지
-
삭제 : 리프에서만 삭제 하고 필요 시 재분배 or 합병
4-2. B+ 트리 삭제 예
43 삭제
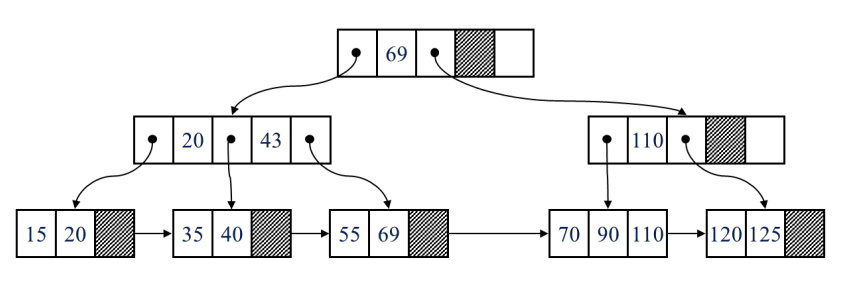
125 삭제 (재분배)
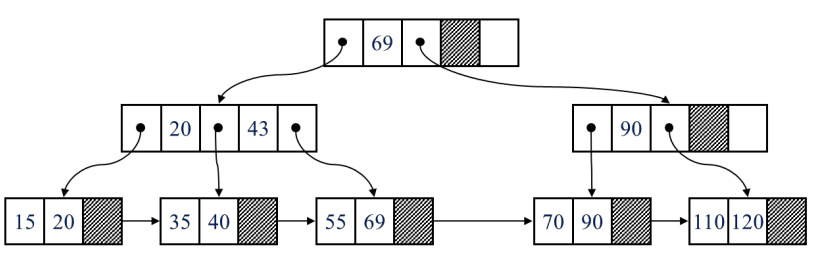
55 삭제 (합병)
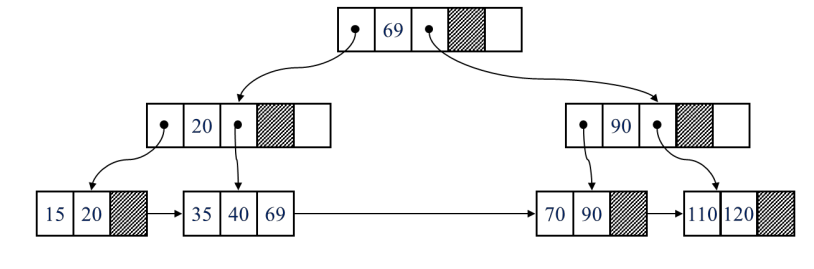
5. 해시 인덱스
- B+ 트리 탐색 I/O = h+1, 해시 인덱스 탐색 I/O = 1
5-1. 버킷 해싱
-
버킷 = page의 모음
-
버킷 해싱 : 키 --> 버킷 주소
-
충돌 : 상이한 레코드들을 같은 주소로 변환. 동거자가 됨. 충돌 시 마다 I/O 추가
-
버킷 만원 시 오버플로 버킷을 연결함
5-2. 확장성 해싱
충돌에 대처하여 레코드 검색 최대 2번의 I/O만 발생
- 모조키 : 확장성 해싱 함수. 키 값 = 일정 길이의 비트 스트링 --> 모조키로 변환

-
모조키의 처음 d 비트를 디렉터리 인덱스로 사용
-
디렉터리 : 헤더에 현재 디렉터리 전역 깊이 d 유지. 2^d개 버킷 주소를 가짐
-
버킷 : 헤더에 현재 버킷 깊이 p 유지

5-3. 확장성 해싱 삽입 (버킷 크기 = 2 레코드 일 때)

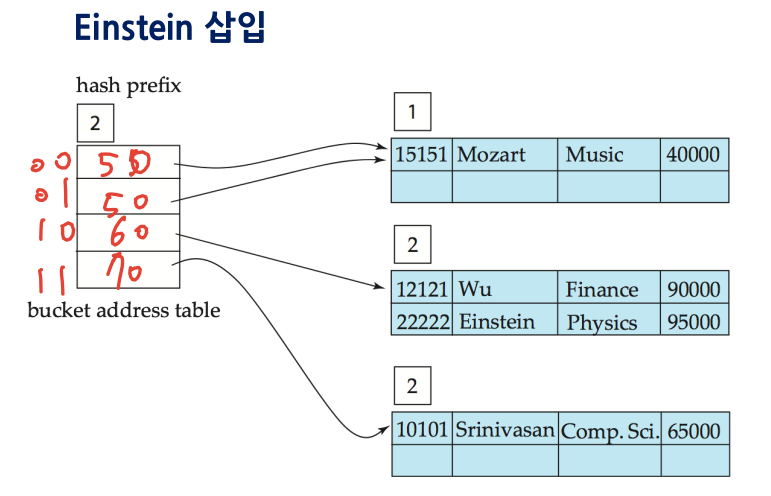

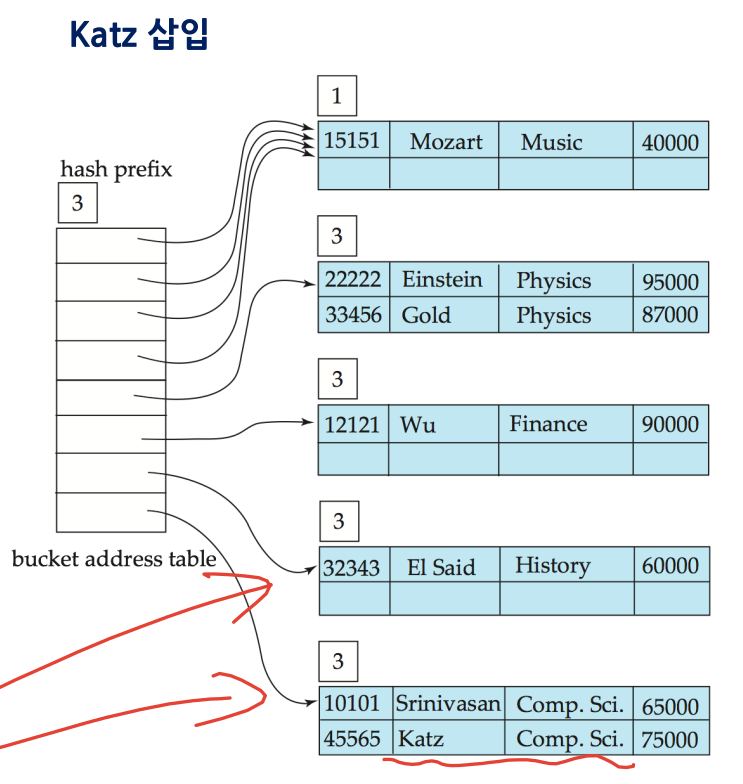

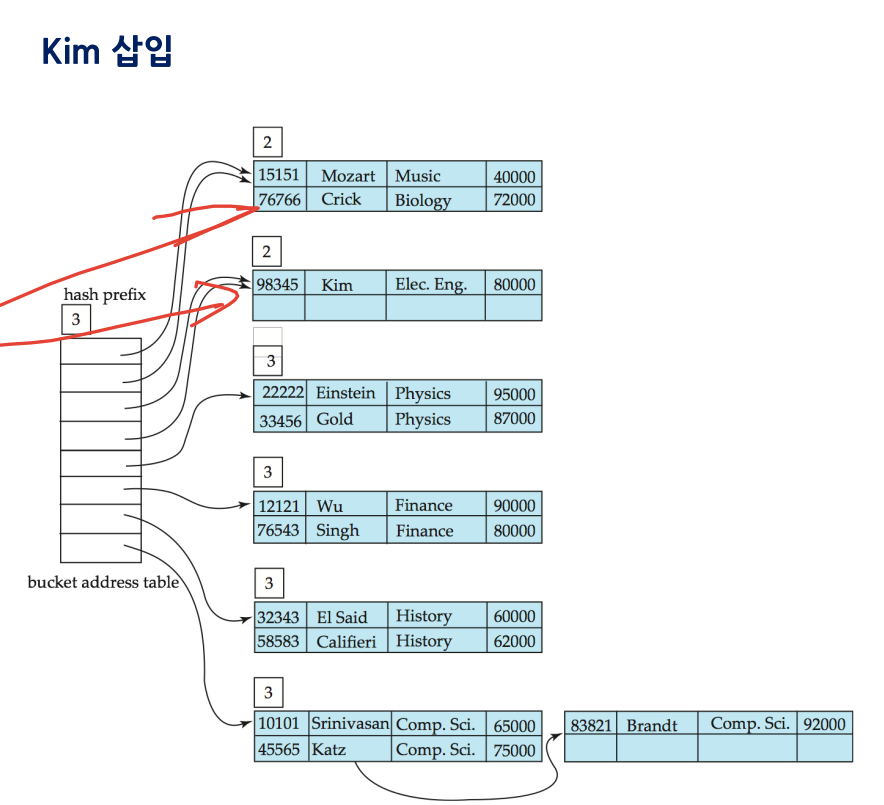
6. 비트맵 인덱스
애트리뷰트의 값이 몇가지 안될 때 사용한다
- 예 : 소득 수준, 성별, 국가
6-1. 비트맵 인덱스 질의 예
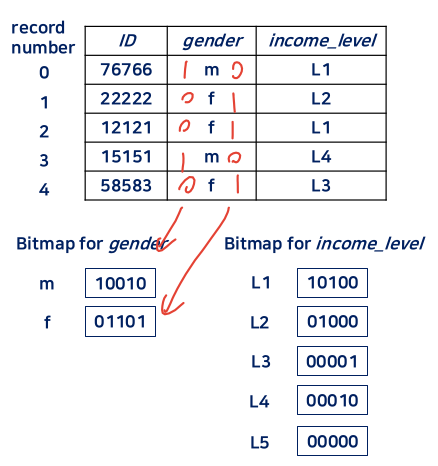
-
gender = 'm' AND income_level = 'L1'
10010 AND 10100 = 10000 -
income_level = 'L1' OR income-level = 'L2'
10100 OR 01000 = 11100 -
income_level != 'L1'
NOT 10100 = 01011
6-2. 비트맵 인덱스에서의 삭제
-
존재 비트맵 : 삭제할 레코드 = 0
ex) 2번 레코드 삭제 : 11011 -
질의 실행 시 항상 존재 비트맵과 AND 연산을 수행한다
-
널 비트맵 : 널 값을 기록
ex) 4번 레코드 성별이 NULL이라면, Bitmap for gender = 00001
7. R-Tree
- 다중키 화일 방식으로 공간을 B-Tree 형태로 표현한 것
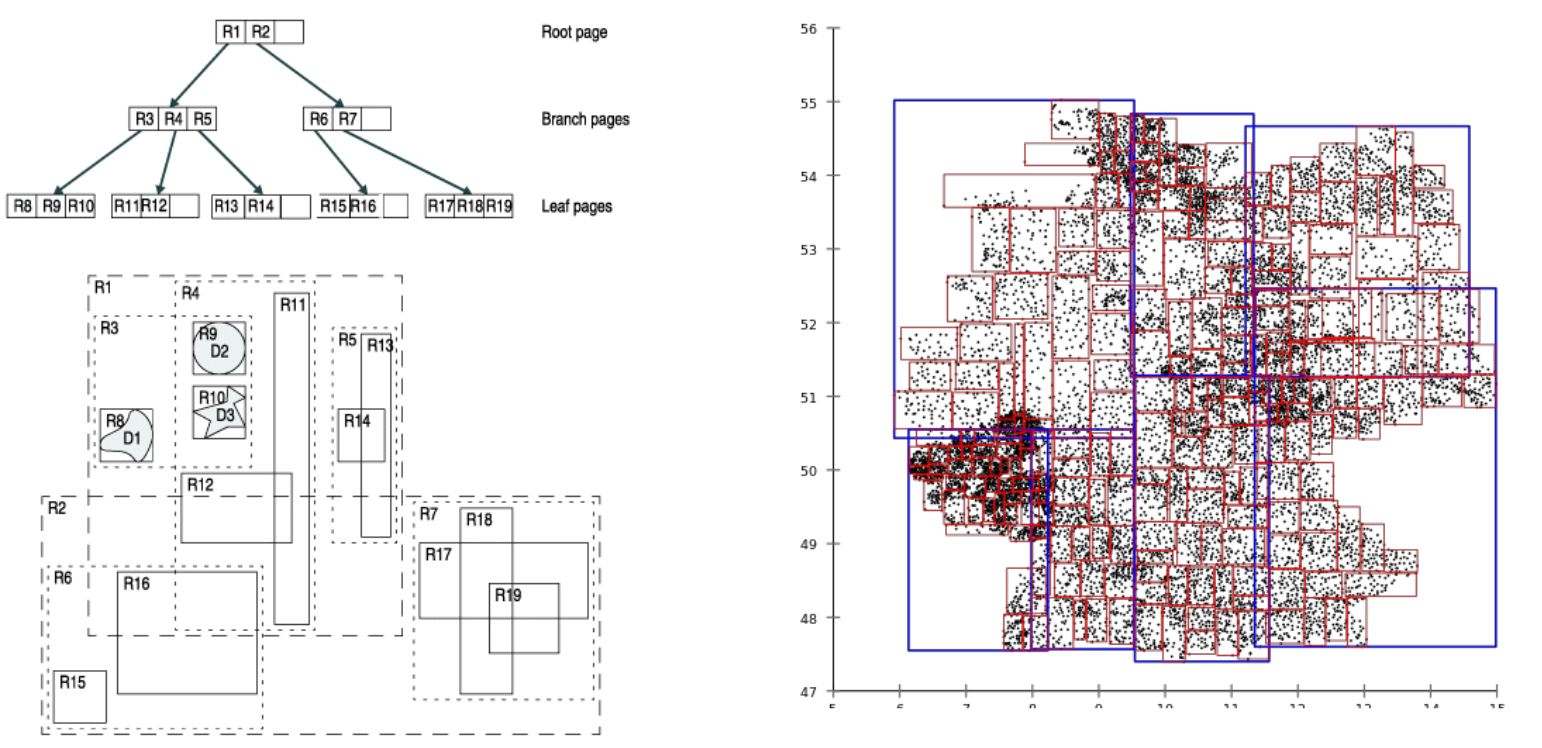
8. 기타
8-1. SQL에서 인덱스 생성 및 삭제
B-Tree
CREATE INDEX my_index ON 학생(학과);
CREATE UNIQUE INDEX stdno_index ON 학생(학번);
DROP INDEX my_index;R-Tree(SQLite)
CREATE VIRTUAL TABLE demo_index USING rtree(
id,
minX, maxX,
minY, maxY
);Bitmap index(Oracle)
CREATE BITMAP INDEX grade_idx ON 학생(학년);8-1. 인덱스별 적합한 질의
-
B+ Tree : point, range
-
hash : point
-
bitmap : point