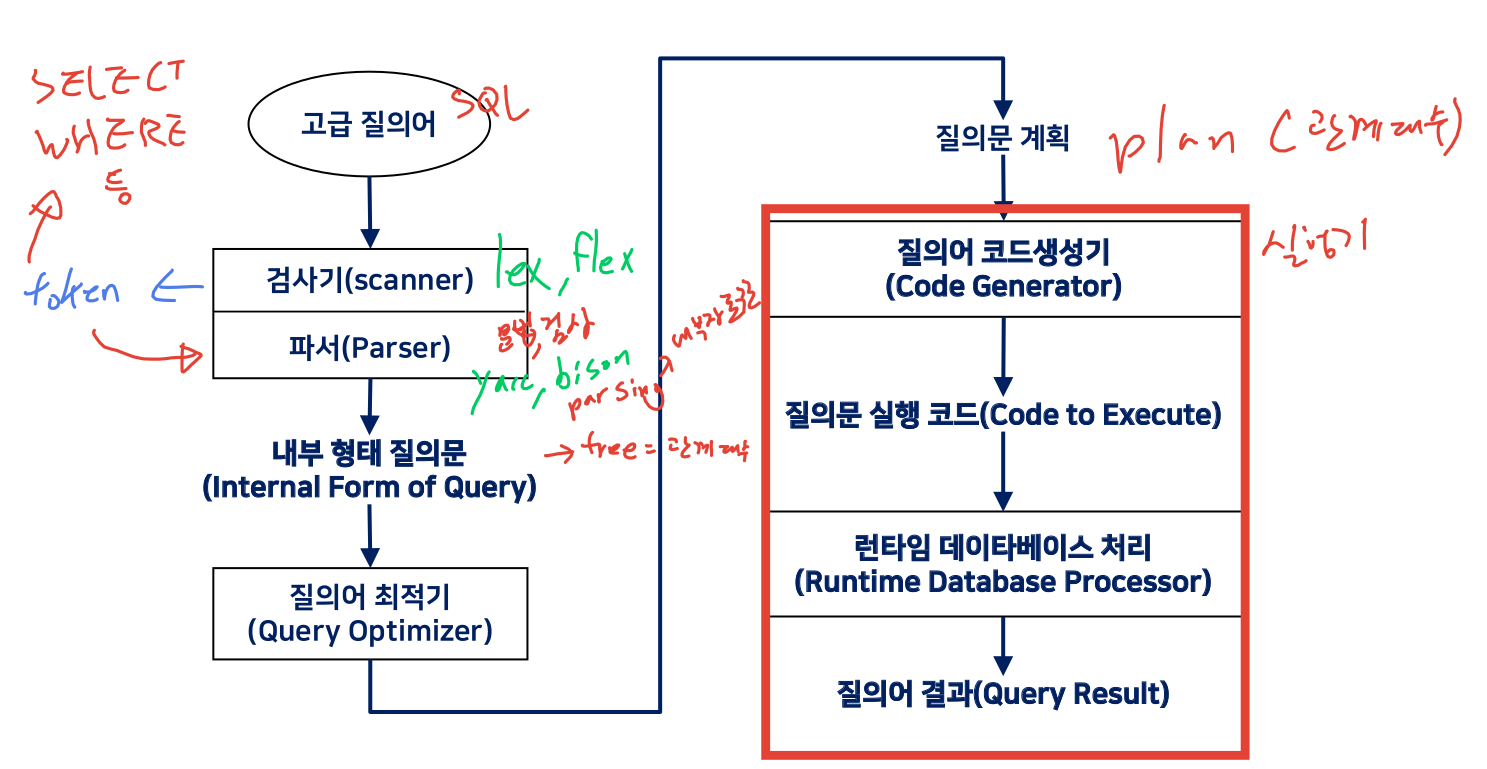
1. 질의어 처리 과정
2. 질의 최적화
-
성능측정 :
i. 디스크 I/O 횟수
ii. 중간 결과의 크기
iii. 응답시간 -
질의어 최적화 과정
i. 질의문 내부표현 (파싱의 결과로 관계대수와 동등한 트리)
ii. 효율적 내부 형태로 변환
iii. 후보 프로시저 선정
iv. 질의문 계획 평가 및 결정
2-1. 질의문의 내부 표현
질의문을 컴퓨터가 처리하기 적절한 형태로 변환
- 부수적 구문과 실제 처리에 불필요한 부분 제거 작업을 포함 한다
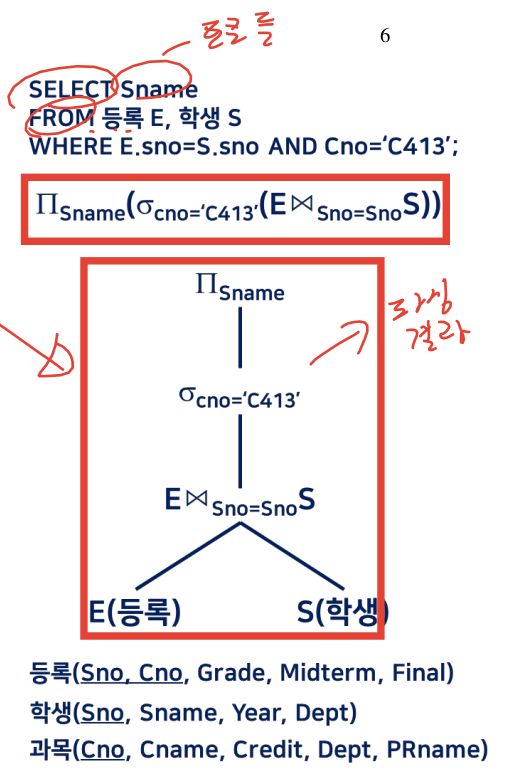
2-2. 질의문 트리
내부 표현 형태는 트리구조로 표현 가능. 이때 관계 대수를 사용한다
-
질의문 트리 = 내부표현형태 = 실행계획 = Plan
-
리프노드 : 피연산자 릴레이션
-
내부노드 : 관계 대수 연산자
-
실행 :
i. 릴레이션이 모두 사용 가능한 서브트리에 대해 먼저 연산
ii. 서브트리를 릴레이션으로 대체
iii. 루트 노드 실행 시 질의문 실행 결과 완료
>> 파이프라인 형태로 동작한다
2-3. 효율적 내부형태로 변환
변환 규칙에 따라 결과는 같지만 처리가 더 효율적인 형태로 변환한다
- 변환 규칙의 종류:
i. 문법적
ii. 추론적
iii. 의미적
예)
SELECT Sname
FROM S, E
WHERE S.Sno=E.Sno AND Cno='C413'|S|=100, |E|=10000, |E.Cno='C413'|=50, 메인메모리 용량 50 투플일 때


2-4. 후보 프로시저 선정
프로시저 : 최종 내부표현을 실제로 실행시킬 과정
-
실행을 고려한 질의문 계획 결정 시 고려사항
i. 인덱스 등 접근 경로의 존재
ii. 저장 데이터 값의 분포
iii. 레코드의 물리적 집중 -
최적기는 내부 표현에 사용된 각 연산자에 대해 하나 이상의 후보 프로시저 선정 가능
>> 접근 경로 선택 : 특정 레코드를 찾기 위한 구조
예) 조인 프로시저, 실렉트 프로시저 등
>> 미리 정의된 프로시저 고려.
예) Selection : 후보키 비교 기초 프로시저, 인덱스 필드 기초 프로시저 등
2-5. 질의문 계획의 평가 및 결정
후보 질의문 계획을 평가하고 최소 비용 계획을 결정
-
질의문 하나에 여러 후보 Plan 존재 가능. 휴리스틱을 통해 제한된 수의 후보를 생성 후 선택
-
비용 계산식
i. 디스크 I/O 비용 (중간 저장 비용 포함)
ii. 계산 비용 (CPU 시간)
iii. 통신 비용 -
예전에는 I/O 비용만 고려했지만 현재는 계산 비용도 같이 고려
3. 내부 형태 변환 규칙
효율적이면서 동등한 관계대수로 변환
- 논리곱(AND)로 연결된 실렉트 조건 = 일련의 개별적 실렉트 조건

- 실렉트 연산은 교환적

- 연속적인 프로젝트 연산 = 마지막 프로젝트만 실행
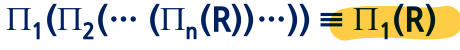
- 실렉트 조건 c가 프로젝트 애트리뷰트만 포함한다면 교환적

- 실렉트 조건이 조인이나 카티션 프로덕트에 관련된 릴레이션 하나에만 국한 = 조인조건

- 실렉트 조건 c=(c1 AND c2) c1은 R, c2는 S의 애트리뷰트만 포함하면 조인을 카티션 프로덕트로 교환

-
X, ∪, ∩, ⑅은 교환적
-
애트리뷰트 리스트 L=(L1,L2) L1은 R에, L2는 S에 포함
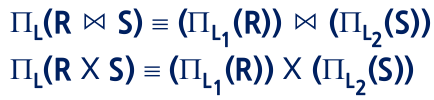
- 집합 연산 와 관련된 실렉트는 다음과 같이 분배

- 합집합과 관련된 프로젝트는 분배

- ∪, ∩, ×, ⑅는 연합적(실행순서 상관 없음)

- OR로 연결된 조건식을 AND로 연결된 논리곱 정규형으로 변환 가능

3-1. 초기 트리를 최적화된 트리로 변환
-
논리곱으로 된 조건을 가진 실렉트 연산은 분해(1)
-
실렉트 연산 먼저 실행되도록 변환(2,4,5,8)
-
중간 결과가 작은 실렉트 연산이 가장 먼저 수행되도록 재정돈
-
카티션 프로덕트 연산 다음에 바로 실렉트 연산이 나오면 조인연산으로 통합(5)
-
프로젝트 연산은 가능한 한 애트리뷰트를 분해해서 개별적 프로젝트로 변환(4,7)
-
OR로 연결된 조건식은 논리곱 정형식으로 변환(12)
4. 질의 변환 예

- 논리곱 연결된 실렉트 조건 분해및 중간 결과 작은 실렉트 재정돈
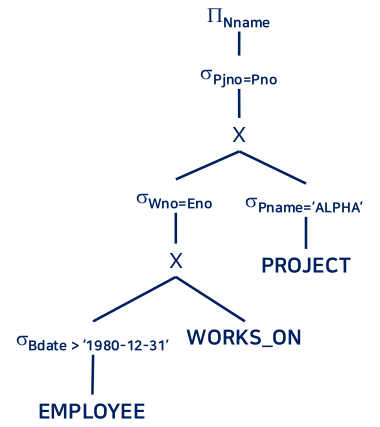
- 중간 결과가 작은 실렉트 먼저 수행 및 카티션 프로덕트, 실렉트 조인 통합
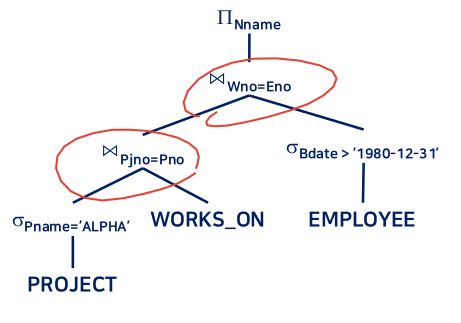
- 프로젝트 분해
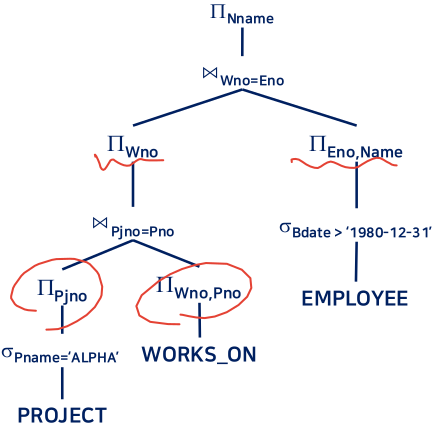
5. 실렉트 연산의 구현
-
선형 탐색 : 주먹구구식
-
이원 탐색 : 동등 비교, 정렬된 데이터
-
기본 인덱스 또는 해시키 이용 포인트 쿼리
-
기본 인덱스 이용 레인지 쿼리
-
집중 인덱스 이용 복수 레코드 쿼리
-
보조 인덱스 이용 유일성 인덱스(단일 레코드)/비유일성 인덱스(복수 레코드)
6. 조인 연산의 구현
- 중첩루프
- 인덱스 검사
- 해시 검사
- 정렬/합병
- 기법들의 조합
-
n원 조인 : n개의 릴레이션 조인
-
R = n개 투플을 가진 외부 릴레이션, S = m개 투플을 가진 내부 릴레이션일 때 R.A=R.B 정렬 가정
-
실제 DB는 버퍼 효율을 높혀 page I/O를 감소시키기 위해 투플 단위가 아닌 블럭 단위로 block nested loop 실행한다
6-1. 중첩 루프
I/O = n*m으로 비용이 가장 큼
6-2. 인덱스 검사
내부 릴레이션의 애트리뷰트가 인덱스됨
I/O = n + n(h+1)
6-3. 해시 검사
내부 릴레이션의 애트리뷰트가 해시 인덱스됨
I/O = n + n(1+1)
6-4. 정렬 합병
외부 내부 릴레이션 모두 애트리뷰트에 대해 정렬
I/O = n+m
7. 프로젝트 연산의 구현
애트리뷰트 리스트로 프로젝트 --> 정렬 --> 중복 제거
8. 비용 함수
-
질의문 계획의 비용을 계산하기 위해선 정보가 필요
-
비용 함수가 필요로 하는 정보 유지 = 카탈로그
i. 파일 크기
ii. 레코드 수(r), 블록 수(b), 블록 내 레코드 수(br)
iii. 접근 방법과 접근 애트리뷰트, 정렬/인덱스/해시 여부
iv. 인덱스 애트리뷰트 값에 대해 상이한 값의 수(d)
v. 검색 투플 수 : 키 애트리뷰트(s=1) 키가 아닌 애트리뷰트(s=r/d) -
비용
선형 탐색 : 키 일때 = b/2, 키 아닐 때 = b
이원 탐색 : log2 b
기본 인덱스 : x + 1
해싱 함수 : 1, 확장성 시 1+1
9. 의미적 질의 최적화
구문 변환 규칙과 스키마 제약조건을 이용한 최적화
예1)
SELECT Sname
FROM S
WHERE Year >= 5무결성 제약조건에 따라 학년의 범위는 1~4. 결과가 없음을 예측 가능
예2)

S.Sno는 기본 인덱스이고 E.Sno는 외래키 일때 == PROJECT Cno(E)


