
Graph as matrix
Linear algebra의 관점에서 바라보기
- Node2vec과 RandomWalk를 그래프의 관점에서 바라보자
PageRank (aka the Google Algorithm)
-
How do you represent the web?
-
Nodes = Web Pages
-
Edges = Hyperlinks
-
이전에는 정적 웹페이지와 링크의 연결로 web이 구성되어 있었음
-
비슷한 방식으로 논문과 인용을 Node, Edge로, Wiki의 정보와 Link를 edge로 사용할 수도 있음
What Does Web Look Like
- Web은 방향 그래프
- 어떤 웹 페이지가 더 중요할 것인가?
- 어떤 링크 구조를 사용해 우선순위를 매길 수 있을 것인가
Link Analysis Algorithms
-
Node의 중요성을 정량화하는 알고리즘
-
Links as Votes!
In-coming Link가 더 중요하다고 할 수 있음
그러나 모든 In-Coming Link는 모두 다른 가치를 지닐 것
이는 Recursive problem -> Node의 중요성에 따라 달라지기에
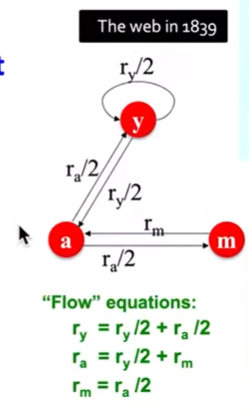
The Flow Model
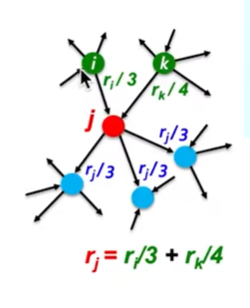
- 각 Link는 source page에 따라 중요도가 나뉨
- 만약 Page I가 중요도 ri를 갖고 di개의 out-links를 가진다면, 각 link는 ri/di의 동등한 중요도를 가짐
- 즉 중요성은 자신으로 부터 향하는 Link 들의 중요성으로부터 구해지고, 자신이 가리키는 문서를 향해 동등하게 분배 됨
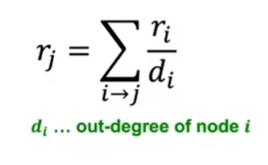
- 다음과 같은 공식으로 정리
이를 연립방정식으로 푸는게 아닌, 행렬의 개념으로 풀이가 가능
Matrix Formula
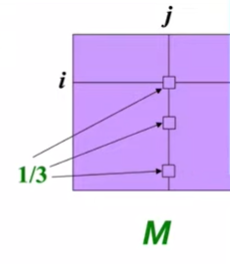
- i에서 j로 Link가 향할때 열의 합이 1인 matrix M을 열확률인접행렬이라고 칭함

- 중요도 행렬인 ri를 정의하면 rj를 단순히 행렬의 곱으로 구할 수 있음
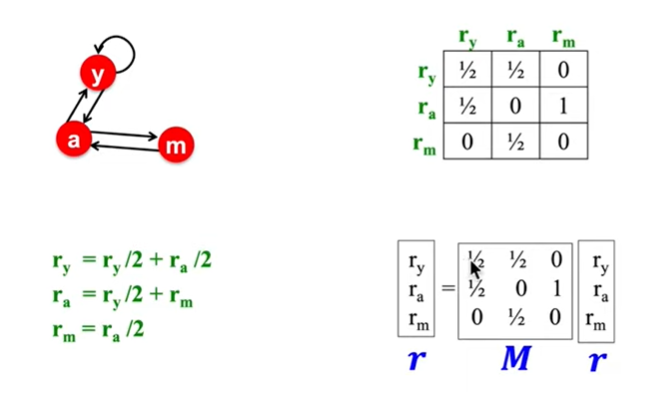
- 마치 Markov chain처럼 equation 됨
- 이는 결론적으로 Random Walk의 최종 목적지처럼 결론 되어짐
- 수학적으로, 알고리즘 적으로 결국 동일한 결과라는 것
- p(t+1) = M * P(t) equation을 극한으로 한 결과가 수렴한다는 것

-
이는 Eigenvector equation으로 또 다시 공식화 됨
-
고윳값이 1인 고유벡터를 구하면 되는 것
-
R = Limiting distribution = Principal Eigenvector of M
-
결국 그래프이론도 수학에 대한 다른 관점인 것
