🚴♂️Dynamic Programming이란
: 큰 문제를 작은문제로 나누어 푸는 문제를 일컫는 말. '다이나믹'이라는 단어는 이 기법과 아무런 상관이 없다.
Divide and Conquer(분할정복)과 다른 점❔
작은 문제가 중복이 일어나는지 안일어나는지가 차이가있다.
분할 정복은 문제를 분할했을 때 겹치는 문제가 발생하지 않지만, DP는 겹치는 문제가 발생하기 때문에 메모이제이션 등이 필요하다.
Dynamic Programming의 조건❔
- 작은 문제가 반복이 일어나는 경우
- 같은 문제는 구할 때마다 정답이 같다.
✔ 일반 피보나치 수열 코드
public class Fibonacci{
static int fibonacci(int n){
if(n == 0) return 0;
if(n == 1) return 1;
return fibonacci(n - 2) + fibonacci(n - 1);
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
System.out.println(fibonacci(N));
}
}
이런 일반 피보나치 수열의 알고리즘은 N이 작은 함수 호출로 갈수록 그 호출의 횟수가 점점 증가한다. (불필요할 정도로 커짐)
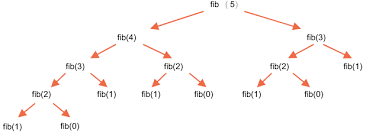
그 이유는 위의 그림으로 이해할 수 있는데, f(5)의 값을 구하기 위해 f(4)와 f(3)의 값을 알아야 한다. 그런데 f(4)의 값을 구할 때도 f(3)과 f(2)의 값을 알아야 하기 때문에, f(4)를 계산해냈을 시점에서 우리는 이미 f(3)이 뭔지도 계산했다. 그러나 뒤에 f(3)을 다시 계산할 때 우리가 했던 짓을 다 잊어버리고 다시 계산하고 있다.
이런 식으로 기하급수적으로 늘어나는 호출 횟수 때문에 f(N)을 구하는 데는 지수 시간의 시간복잡도가 발생한다.
이 문제를 해결하기 위해서는 메모이제이션(Memoization) 기법을 사용할 수 있다.
✔ Memoization을 이용한 피보나치 수열 알고리즘
public class Fibonacci{
static int[] dp = new int[1000];
static int fibonacci(int n){
if(n == 0) return 0;
if(n == 1) return 1;
if(dp[n] != 0) return dp[n];
dp[n] = fibonacci(n - 2) + fibonacci(n - 1);
return dp[n];
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
System.out.println(fibonacci(N));
}
}피보나치 함수에서는 먼저 dp[n]을 계산한적이 있는지 확인하고, 계산한적이 있다면 추가 재귀 호출 없이 그 값을 바로 리턴해 버린다.이렇게 하면 한 번 계산했던 값은 두 번 다시 계산할 필요가 없으므로, f(N)을 구하는 데 O(N)의 시간만이 필요하다.
✔ 반복문을 이용한 피보나치 수열 알고리즘
public class Fibonacci{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int[] dp = new int[N + 1];
dp[1] = 1;
for(int i = 2;i <= N;i++)
dp[i] = dp[i - 1] + dp[i - 2];
System.out.println(dp[N]);
}
}이 코드는 재귀 호출 없이 반복문을 통해 구한 알고리즘이다.
이번에는 N보다 작은 피보나치 항의 값들만 정확히 알고 있다면 f(N)을 구하는 데도 문제가 없다는 점을 이용하여 f(2)부터 f(N)까지의 값을 차례대로 구한다.
이렇게 반복문을 사용하는 것 역시 O(N)의 시간복잡도가 걸린다. 한 가지 손해가 있다면, 그냥 구했을 때보다 공간복잡도가 늘어났다는 것인데, 원래는 별도의 메모리가 필요없었지만 이제는 각 항의 값을 기억하고 있어야 하니까 O(N)의 메모리가 필요하다.
탑다운 ⬇(Top-down), 바텀업 ⬆(Bottom-up)
-
탑다운 (재귀 호출 사용)
: 가장 먼저 호출하는 문제는 가장 큰 문제이기 때문에 이런 명칭이 붙음탑다운 방식의 장점은 가독성이 좋고, 본래 점화식을 이해하기 쉽다.
-
바텀업 (반복문 사용)
: 가장 작은 문제들부터 차례차례 답을 쌓아 올려가기 때문에 이런 명칭이 붙음바텀업 방식의 장점은 함수를 별개로 부르지 않아 시간과 메모리를 소량 더 절약할 수 있다는 점이 있다.
[JAVA] 백준 알고리즘 1463번 문제 풀이 (1로 만들기)
https://sanizzang.tistory.com/4
[JAVA] 백준 알고리즘 2294번 문제 풀이 (2294)
https://sanizzang.tistory.com/5
