1932(dp)

첫인상

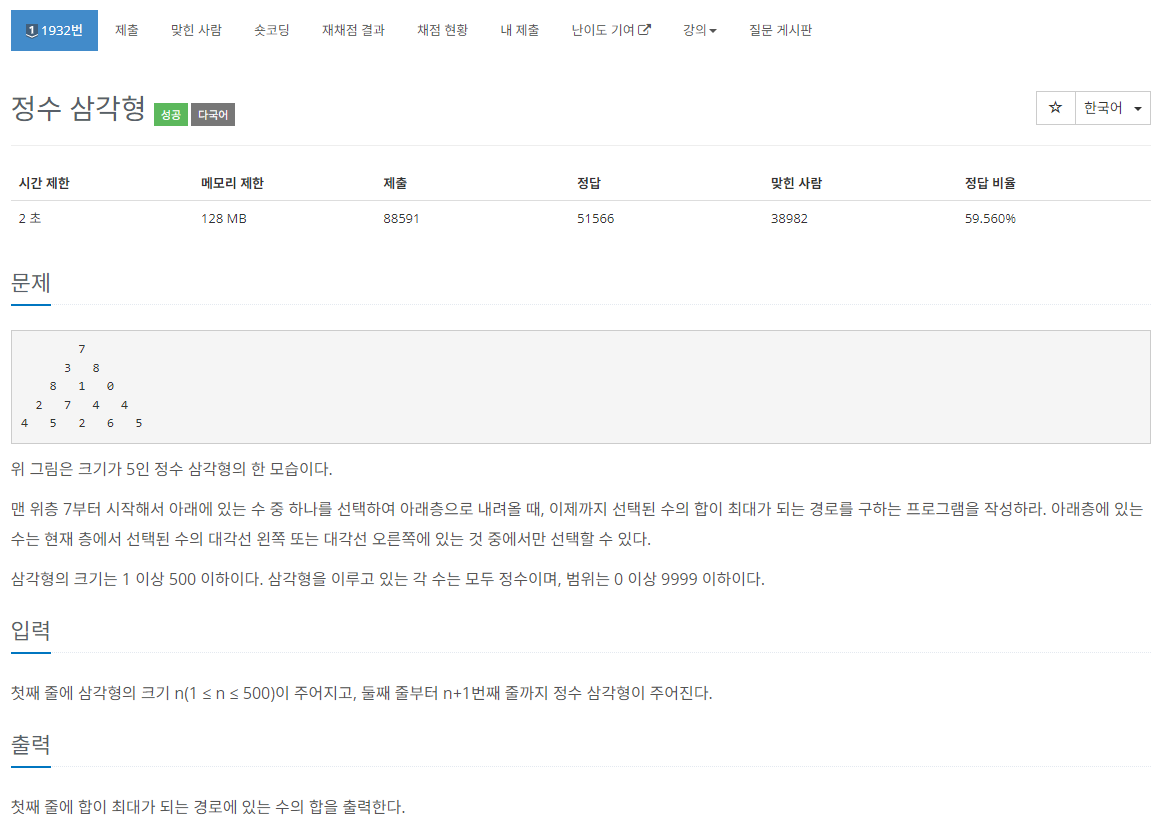
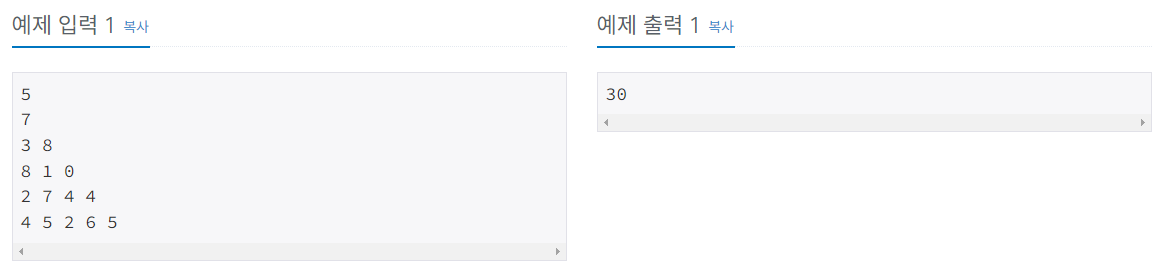
선택된 수의 합이 최대가 되는 경로를 구하는 전형적인 dp 문제다

풀이

변수는 정수 삼각형 하나기 때문에 정수 삼각형을 표현할 수 있는 2차원 dp로 풀어주었다

코드

#include<iostream>
using namespace std;

int nums[505][505];
int dp[505][505];
int n;

void input() {
	cin >> n;

	for (int i = 0; i < n; i++) {
		for (int j = 0; j < i + 1; j++) {
			cin >> nums[i][j];
		}
	}
}

void solve() {
	dp[0][0] = nums[0][0];
	
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < i + 1; j++) {
			dp[i + 1][j] = max(dp[i + 1][j], dp[i][j] + nums[i + 1][j]);
			dp[i + 1][j + 1] = max(dp[i + 1][j + 1], dp[i][j] + nums[i + 1][j + 1]);
		}
	}

	int ans = 0;
	for (int i = 0; i < n; i++) {
		if (ans < dp[n - 1][i]) {
			ans = dp[n - 1][i];
		}
	}

	cout << ans;
}

int main() {
	input();
	solve();
}