3.1 Introduction

2장은 'neighborhood-based methods' 이웃 기반 방법에 대해 살펴봤습니다.
이 방법들은 'instance-based learning method' (인스턴스 기반 방법)으로 효율적인 구현을 위해서 선택적인 전처리 단계를 거치는 것을 제외하곤, 예측을 위한 모델 을 미리 만들지 않습니다. (이런 방법을 lazy learning method 라고 부릅니다)

model-based method에선, supervised, unsupervised learning 방법과 마찬가지로 데이터의 모델 요약이 앞부분에 작성됩니다.
그래서 학습(training)과 예측(prediction) 단계가 확실히 구분됩니다.
이 때 '학습'은 모델 생성 단계로 볼 수 있습니다.

Machine Learning Model 예시

• Decision trees
• Bayes classifiers
• Regression models
• Support vector machines
• Neural networks

대부분의 이 모델들은 collaborative filtering scenario로 일반화될 수 있습니다.
우리가 알고있는 전통적인 classification, regression 문제가 matrix completion(행렬 완성), 또는 collaborative filtering의 특수한 경우이기 때문입니다.

이웃 기반 추천시스템과 비교했을 때 모델 기반 추천 시스템의 장점
1. space efficiency (용량 효율성)
학습된 모델의 크기는 원래의 평점 행렬보다 훨씬 작습니다. 그래서 비교적 적은 용량을 필요로 합니다.
반면 사용자 기반 이웃 방법은 보통 O(m^2)의 공간 복잡도를 가집니다. (m:사용자 수)
아이템 기반 방법은 O(n^2) 의 공간 복잡도

2.traning speed & prediction speed (학습 속도, 예측 속도)
이웃 기반 방법 문제점은 전처리 단계 시간 복잡도가 사용자 수나 아이템 수의 제곱이 됩니다. 반면 모델 기반 시스템은 모델을 훈련할 때 전처리 단계를 처리하는 속도가 훨씬 빠릅니다. 대부분의 경우 compact 하고 요약된 모델이 효율적인 예측을 하는 데 사용될 수 있습니다.

3. overfitting 방지
   overfitting은 머신러닝 알고리즘에서 자주 발생하는 문제입니다. 모델 기반 방법의 요약 접근 방식은 overfitting을 방지하는 데 도움이 될 수 있습니다. 추가로 regularization 을 통해 모델을 robust 하게 만들 수 있습니다.

2장에서 살펴본 이웃기반 방법이 초기 Collaborative Filtering 방법 중 하나였고 단순해서 많이 사용되었습니다. 그러나 요즘은 모델 기반의 기법을 사용하는 것이 일반적이고 특히 'latent factor model'에 기초하게 됩니다.

3.2장 : 의사결정, 회귀트리 활용법
3.3장 : 규칙 기반 협업 필터링 방법
3.4장 : 추천시스템을 위한 naive bayes 모델
3.5장 : 어떻게 다른 분류 방법이 협업 필터링으로 확장될 수 있는지
3.6장 : latent factor model
3.7장 : latent factor model과 이웃 기반 모델 통합
3.8장 : 요약

3.2 Decision and Regression Trees (의사 결정 및 회귀 트리)

decision tree, regression tree 는 데이터 분류에서 자주 사용됩니다. 둘의 차이는 데이터의 타입입니다. decision tree는 dependent variable이 class형 data 일 경우 사용되고, regression tree 는 dependent variable이 numerical 데이터일 경우 사용됩니다.

우선 collaborative filtering 으로 일반화하기 전에, decision tree에 대해서 알아봅시다!

matrix R (mxn) 이 있을 때, 첫 (n-1)열들을 independent variable 이라고 가정하고 마지막 열을 dependent variable이라고 가정해보겠습니다.
( 이 때 모든 변수가 이항이라고 가정)

decision tree 는 independent variable에서 split criteria(분리 기준)로 알려진 계층적 결정 집합을 사용해 데이터 공간을 계층적으로 분리합니다.
univariate decision tree 에서는 분리를 수행하기 위해 한번에 하나의 feature가 사용됩니다.
이렇게 feature 변수를 선택하고 class 변수와 상관관계를 맺으면 각 branch에 있는 데이터 기록들은 더 순수해지게 됩니다.
즉, 다른 클래스에 속한 데이터들이 대부분 분리됩니다.

이렇게 분리된 'quality'는 분리를 통해 생성된 children node 의 가중 평균 Gini index 를 통해 평가할 수 있습니다.
만약 p1,..,pr 이 node S의 r개의 다른 클래스에 속한 데이터 기록의 split 비율이라 한다면, node의 gini index G(s)는 다음과 같이 정의됩니다.

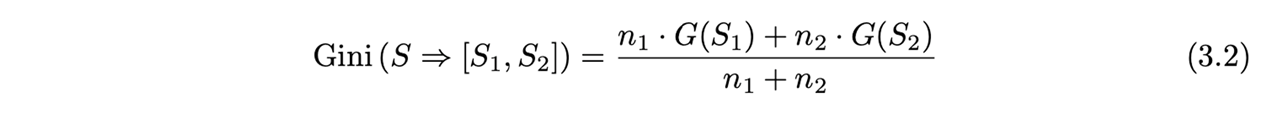
gini index는 0에서 1사이의 값을 갖고 값이 작으면 분별 능력이 좋다는 것을 의미합니다. 분할된 gini index는 children node gini index의 가중 평균과 같습니다.
여기서 노드의 가중치는 노드에 있는 데이터의 수로 정의됩니다.

그렇기 때문에 만약 binary decision tree의 node S의 s1과 s2가 n1과 n2 만큼의 데이터 기록을 갖고 있는 두 children node 라면 S=>(s1,s2)로 분리되는 S의 gini index는 위와 같습니다.

분할을 할 때 가장 작은 gini index를 갖는 attribute이 선택됩니다. 이런 방법은 top-down 방식이 계층적으로 수행되고 각각의 node가 오직 하나의 class에만 속할 때까지 수행하게 됩니다.

즉 test instance를 구분하기 위해 데이터의 independent variable 들은 decision tree의 root부터 leaf 까지의 path를 만드는 데 사용됩니다.

decision tree는 데이터 공간을 계층적으로 분리하기 때문에 test instance는 root부터 leaf까지는 잇는 정확히 하나의 경로를 따릅니다.
결국 leaf의 표시값은 test instance의 class로 기록됩니다.

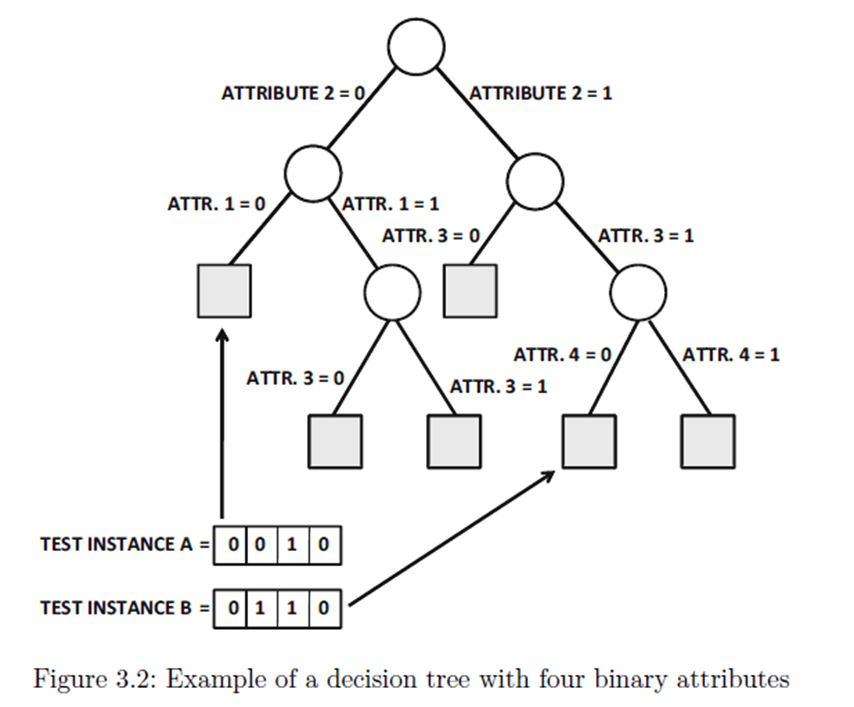
4개의 속성을 가진 decision tree 예시
(이 때, 모든 속성이 분할 할 때 꼭 사용되는 건 아닙니다. 그리고 attribute을 사용하는 순서가 경로마다 다를 수도 있습니다.)
가장 왼쪽 경로는 1,2만 사용하는 것처럼..

결론적으로 계층적인 데이터 분류의 속성 때문에 각각의 test instance들은 유일한 leaf node에 대응되게 됩니다.

3.2.1 Extending Decision Trees to collaborative Filtering

decision tree를 collaborative filterig으로 확장할 때 제일 문제는 '예측할' 항목과 '관측된' 항목이 column별로 feature variable과 class variable로 명확히 구분이 안된다는 점입니다.
게다가 대부분의 항목이 값이 없는 rating matrix는 매우 sparse한 행렬입니다.

그리고 collaborative filtering에서 independent variable 와 dependent variable가 명확히 구분되지 않는데, 어떤 item이 decision tree에 의해 예측돼야 할까요?

후자의 문제는, 각 item에 대해 평점을 예측하는 별개의 decision tree를 구축해 쉽게 다룰 수 있습니다.
m명의 user와 n개의 item의 rating이 기록된 mxn rating matrix R이 있다고 했을 때, dependent인 각각의 attribute을 고정해 나머지 attribute을 고정해 별도의 decistion tree가 만들어집니다.
결국 decision tree의 수 == item 수 (n)

반면, independentㅎ한 feature의 누락 문제는 다루기 더 어렵습니다.
특정 item이 classification attribute으로 사용된 경우를 생각해봤을 때, 임계점보다 평점을 작게 준 모든 사용자는 한 branch에 할당되는 데 반해, rating을 임계점보다 rating을 작게 준 모든 user는 다른 branch에 할당됩니다. 그런데 rating matrix가 sparse하기 때문에 대부분의 사용자는 특정 item에 대한 평점을 갖고 있지 않습니다. 이런 경우엔, decision tree는 더 이상 training data를 정확히 나누지 않게 됩니다. 게다가 이런 접근에 따르면 test instance는 decision tree에서 다양한 path에 대응될 것이고 다양한 path마다 충ㄷ돌되는 예측이 단일한 예측으로 결합돼야 합니다.