1. 개요
-
대칭키 암호를 사용하려고 하면 키 배송 문제(key distribution problem)가 발생한다.
-
키를 보내지 않으면 수신자는 수신한 암호문을 복호화 할 수 없다.
-
그렇다고 암호화 되지 않는 키를 보내면 도청자가 복호화할 수 있다. 이것이 키 배송 문제이다.
-
키 뱅송 문제를 해결하기 위한 방법
- 키의 사전 공유에 의한 해결
- 키배포 센터에 의한 해결(온라인 키 분배)
- Diffie-Hellman 키 교환에 의한 해결
- 공개키 암호에 의한 해결
2. 키의 사전 공유에 의한 해결
- 키 사전 분배란❓ 키 관리기관(TA, trusted authority)이 사전에 임의의 두 사용자(A, B)에게 비밀 경로를 통하여 임의 키 Ka,b =Kb,a를 선택하여 전달하는 방법이다.
- 일반적으로 TA와 네트워크 상의 모든 사용자 사이에 안전한 통로가 필요하며, TA는 물론 사용자들도 많은 키를 관리해야 한다.
3. 키배포 센터에 의한 해결(온라인 키 분배)
🅰 개요
- 암호 통신이 필요해질 때마다 통신용 키를 키배포 센터(KDC, key distribution center) 라는 신뢰받는 제 3자에게 의뢰해서 개인과 키배포 센터 사이에서만 키를 사전에 공유하는 방법.
- n 명의 사원이 있다면 n 개의 컴퓨터 데이터베이서에 저장한다.
🅱 단계별 순서
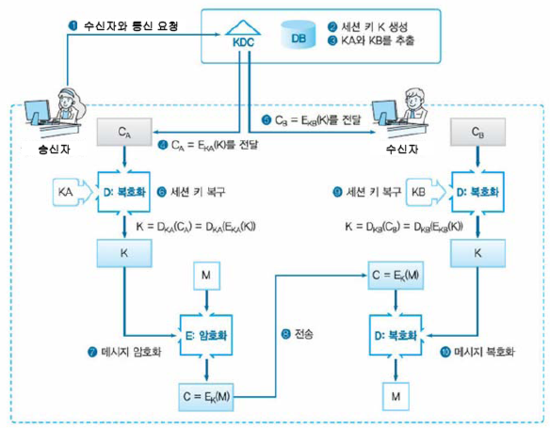
- 송신자는 키배포 센터에서 수신자에게 통신하고 싶다고 신청한다.
- 키배포 센터는 의사난수 생서기를 이용하여 세선키 K를 생성한다. (이번 통신만을 위한 일시적인 키)
- 키배포 센터는 데이터베이스에서 송신자의 키(KA)와 수신자의 키(KB)를 꺼낸다.
- 키배포 센터는 송신자의 키를 이용하여 세션키를 암호화해서 송신자에게 보낸다.
- 키배포 센터는 수신자의 키를 사용해서 세션키를 암호화해서 수신자에게 보낸다.
- 송신자는 키배포 센터에서 온 세션키를 복호화해서 세션키를 얻는다.
- 송신자는 세션키를 이용하여 수신자에게 보낼 메일을 암호화해서 수신자에게 보낸다.
- 수신자는 키배포 센터에서 온 세션키를 복호화해서 세션키를 얻는다.
- 수신자는 세션키를 사용하여 송신자에게 온 암호문을 복호화 한다.
- 송신자와 수신자는 세션키를 삭제한다.
4. Diffie-Hellman 키 교환에 의한 해결
🅰 개요
- 공개키 암호방식의 개념을 이용하여 두 사용자 간에 공통의 암호화키를 안전하게 공유할 수 있는 방법을 제시하였다.(최초의 비밀키 교환 프로토콜)
- 양쪽 통신주체가 KDC 없이 대칭 세션키를 생성한다.
- 유한체상의 이산대수 문제(DLP)를 풀기 어렵다는 사실이 Diffie-Hellman 키 교환을 뒷받침한다.
🅱 절차
- 앨리스가 소수 p, 1부터 p-1안에서 정수 g를 선택하고 밥이랑 공유한다.
- 앨리스가 정수 a를 선택하고, 이 정수는 공개되지 않고, 밥 또한 알지 못한다.
- 앨리스가 A = g^a mod p를 계산한다.
- 밥 또한 정수 b를 선택하여 B = g^b mod p를 계산한다.
- 앨리스와 밥이 서로에게 A와 B를 전송한다.
- 앨리스가 B^a mod p를 계산하고, 밥이 A^b mod p를 계산한다.
- 이렇게 구한 값은 결국 g^ab mod p라는 세션에 사용될 대칭키이다.
📌 예제
- 파란색은 공개된 정보, 빨간색은 공개되지 않는 정보이다.
🔶 Diffie-Hellman의 안전성
- 이산대수 공격
- 키 교환의 안전성은 이산대수 문제를 풀기 어렵다는데 기반을 두고 있다.
- 도청자가 A와 B를 가로챌 수 있다. 만약 도청자가 g^a mod p에서 a를 구하고 g^b mod p에서 b를 구한다면 비밀키가 더이상 비밀이 되지 못한다.
- 서비스 거부 공격(DoS)
- DH 기법은 지수 함수에 기초하고 있으므로 계산이 복잡할수록 비밀키 생성에 큰 지연 시간이 발생할 수 있다.
- 따라서 DH기법은 제 3자에 의한 DoS 공격에 대한 취약점을 가지고 있다.
- 중간자 공격
- 키 교환 프로토콜은 인증단계가 없기 때문에 중간자 공격에 취약하다. 이런 공격을 막기 위해서는 전자서명과 공개키 인증서를 이용한다.
5. 공개키 암호에 의한 해결
- 암호화키와 복호화키가 다른 것이다.
- 수신자는 미리 암호화키를 송신자에게 알려주고 이 암호화키는 도청자에게 알려저도 괜찮다.
- 복호화할 수 있는 것은 복호화키를 가지고 있는 사람(수신자)뿐이다.
