[AI] AlexNet (2) - ReLU nonlinearity

SAsgaNAmabeer·2021년 5월 13일
1

AlexNet

목록 보기
2/2
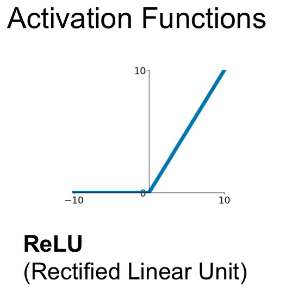
post-thumbnail

이번 글에서는 지난 포스트에서 읽었던 통칭 AlexNet 논문에서 등장하는 ReLU nonlinearity(비선형성)에 대해서 다뤄보려고 한다.



비선형성(Nonlinearity)?

선형성(linearity)의 정의(from wikipedia)

  • 직선처럼 똑바른 도형, 또는 그와 비슷한 성질을 갖는 대상이라는 뜻으로, 이러한 성질을 갖고 있는 변화등에 대하여 쓰는 용어이다. 함수의 경우, 어떠한 함수가 진행하는 모양이 '직선'이라는 의미로 사용.
  • 수학에서 선형성에 대한 정의는 다음과 같다.
    함수 f에 대해,
    ⅰ) 가산성(Additrevityly), 즉, 임의의 수 x,y에 대해 f(x+y)=f(x)+f(y)+f(x+y) = f(x)+f(y)^+가 항상 성립하고
    ⅱ) 동차성(Homogeneity), 즉, 임의의 수 x와 α에 대해 f(αx)=αf(x)f(αx) = αf(x)가 항상 성립할 때
    함수 f+f^+는 선형이라고 한다.

싸늘하다. 가슴에 비수가 날아와 꽂힌다. 하지만 걱정하지 마라. 직접 대입하는게 일반식 이해보다 빠르니까.


상수 대입해서 확인하기

여기 f(x)=xf(x)=x라는 함수와 f(x)=x2f(x)=x^2이라는 함수가 있다. 이 둘이 가산성과 동차성을 만족하는지 확인해보자.

  • f(x)=xf(x)=x
    가산성: f(1+2)=f(1)+f(2)=>f(1)=1,f(2)=2,f(3)=3f(1+2) = f(1) + f(2) => f(1)=1, f(2)=2, f(3)=3 이므로 만족
    동차성: f(5∗1)=5∗f(1)=>f(1)=1,f(5)=5f(5*1) = 5 * f(1) => f(1)=1, f(5)=5 이므로 만족
    따라서, 함수 f(x)=xf(x)=x 는 선형성을 가진다.
  • f(x)=x2f(x)=x^2
    가산성: f(2+3)=f(2)+f(3)=>f(2)=4,f(3)=9,f(5)=25f(2+3) = f(2) + f(3) => f(2)=4, f(3)=9, f(5)=25 이므로 만족하지 않음.
    동차성: f(5∗2)=5∗f(2)=>f(2)=4,f(10)=100f(5*2) = 5 * f(2) => f(2)=4, f(10)=100 이므로 만족하지 않음.
    따라서, 함수 f(x)=x2f(x)=x^2 는 비선형성을 가진다.


    가산성과 동차성을 만족하면 선형성을 가지는 것이고, 반대로 둘 중 하나라도 만족하지 못 한다면 선형성을 가지지 못 한다. 즉, 비선형성(nonlinearity) 을 가지게 되는 것이다.
    그렇다면 이쯤에서 드는 생각이 있다(적어도 필자는 그랬다). '어차피 직선이면 선형이고 직선이 아니면 비선형 아닌가? 뭐하러 힘들게 동차성이니 가산성이니 따지지?' 라는 생각이 들었고 검색을 해 봐도 대부분의 경우 선형과 비선형을 직선이냐 아니냐로 표현하고 있었다. 하지만 어떤 강의영상을 발견했고 이런 단순한 생각이 맞지 않는 경우가 있음을 확인했다. 한번쯤 확인해보시면 좋을 영상이다. 적어도 필자보다 선형과 비선형의 차이를 잘 설명해주신다.


Activation function?

그렇다면 활성화 함수(Activation function)라는 것은 무엇이고 딥러닝에서 활성화 함수가 왜 필요할까? 먼저, 활성화 함수라는 표현은 인간의 뉴런이 신호를 전달하는 방식에서 따왔다.

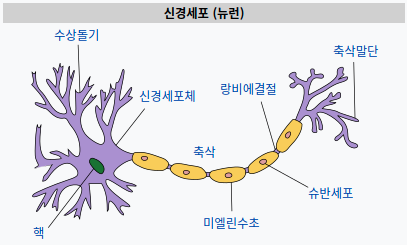
그림 출처 - wikipedia.org

뇌를 구성하는 신경 세포 뉴런이 수상 돌기(=가지 돌기)에서 신호를 받아들이고, 이 신호가 일정치(역치값) 이상의 크기를 가지면 축삭돌기를 통해 신호를 전달한다. 인공 신경망에서는 이를 임계치(threshold)라는 개념으로 도입했다. 신경망에서 각 입력값은 가중치와 곱해져 인공 뉴런에 보내진다. 그렇게 곱해진 값의 전체 합이 임계치를 넘으면 인공 뉴런은 1을 출력하며, 아닌 경우에는 0을 출력한다. 이 때 임계치를 넘는지 넘지 않는지 계산하는 것이 활성화 함수이다. 태초의 인공 신경망인 퍼셉트론(Perceptron) 에서는 계단 함수(Step Function)를 활성화 함수로 사용했다. 즉, 활성화 함수라는 것은 input이 수용할 만한지 판별하는 수문장 같은 역할이라고 볼 수 있겠다.



Saturating nonlinearity

이전 글에서 논문을 읽다 보면 포화(saturating) 비선형, 비포화(non-saturating) 비선형 이라는 개념이 등장한다.

포화(Saturation) 비포화(non-Saturation)?

활성화 함수로 특정 비선형 함수(e.g., sigmoid, tanh...)를 적용한 신경망에서 반복해 학습시키다 보면 가중치(w)가 업데이트 되지 않는 지점(즉, 업데이트량=접선의기울기=0)이 발생한다. 이러한 현상을 Saturation 이라고 부른다. 말하자면, Saturation(현상)으로 인해 Vanishing Gradient Porblem(결과)이 발생하는 것이다. 그렇다면 어떤 특징이 있기에 sigmoid, tanh 와 같은 함수는 Vanishing Gradient(이하 VG)가 발생하고 ReLU에서는 발생하지 않는지 알아보자.

VG(기울기 값이 사라지는 문제)는 인공신경망에서 기울기 값을 베이스로 하는 방법(e.g., Back-propagation)으로 학습시킬 때 문제가 된다. 특히 신경망 전면부의 parameter들을 학습시키고 튜닝하기 어렵게 만든다.
Gradient 기반의 방법은 parameter 값의 변화가 신경망의 출력에 영향을 어느정도 주는지에 따라 parameter 값을 학습한다. 이 때 parameter 값의 변화가 신경망 출력에 아주 작은 변화만 주게 된다면 parameter를 학습하기 어려워진다. 따라서 변화량(=Gradient=미분값)이 매우 작다면, 신경망을 효과적으로 학습시키지 못 하고 오류율을 감소시키지 못 한 채 수렴해버린다.
즉, Gradient가 0에 가까워지면(Vanish 되면), 신경망의 학습 속도는 매우 느려지고, (Global minimum이 아닌)Local minimum에 도달하게 되므로 문제가 되는 것이다.


sigmoid

그림 출처 - Stanford univ. CS231n

바로 이렇게 생긴 녀석이 시그모이드(sigmoid)함수이다. 대표적인 포화 비선형 함수이며,
공식으로는 s(z)=11+e−zs(z)= \frac 1{1+e^{-z}} 라고 표현한다. 요즘은 은닉층(hidden layer)의 활성화 함수로는 거의 사용하지 않고, 이진분류 모델에서 출력층의 활성화 함수 정도로 쓰인다. 과거 가장 많이 사용되던 활성화 함수였지만 지금의 입지를 가지게 된 건 다음과 같은 이유 때문이다.

  • Saturation : Sigmoid는 0<n<10<n<1 의 값을 다루므로 순방향전파(feed-forward)와 역전파(back-propagation)를 반복하다 보면 결과 값이 결국 0으로 수렴할 수 밖에 없다(0.999...0.999...도 무한히 곱하면 결국 0에 가까워지므로).

  • Not zero-centered : (이 개념이 다소 어려움) 'Zero-centered'는 말 그대로 그래프의 중심이 x축과 y축이 만나는 0의 위치에 있는 것이다. 그렇지 않은 경우에는 어떤 문제가 생기는 걸까?
    Neural networks(이하 NN)에서 어느 한 layer의 input은 이전 layer의 output이 된다(입력층과 출력층을 제외). 활성화 함수로 시그모이드를 사용하면 모든 input이 항상 양수가 되어버리는 것이다. 그렇게 되면 역전파(Back-propagation) 시에 문제가 생긴다.

    역전파는 ∂L∂wi=∂L∂f×∂f∂wi\frac {\partial L}{\partial w_i} = \frac{\partial L}{\partial f} \times \frac{\partial f}{\partial w_i} 라는 공식을 거친다.

    ∂f∂wi=xi\frac{\partial f}{\partial w_i} = x_i 이므로, input(=xix_i)이 항상 양수라면 자연스럽게 (1)∂L∂wi\frac {\partial L}{\partial w_i} 와 (2)∂L∂f\frac{\partial L}{\partial f} 가 같은 부호를 가져야만 한다(양쪽 항의 부호가 같아야만 등호가 성립하므로). 즉, (1)과 (2)가 모두 '+' 혹은 '-' 부호를 똑같이 가져야만 등호가 성립한다.
    이것이 의미하는 바는 다음 그림에서 확인할 수 있다.

    그림 출처 - Stanford univ. CS231n

    그림의 그래프에서 파란선이 가장 이상적으로 학습이 진행되는 벡터라고 생각하면 된다. 하지만 상술했듯이 시그모이드를 사용하면 우리는 (+,+) 벡터 혹은 (-,-) 벡터가 강제된다. 따라서, 파란 벡터를 따라가려면 그림과 같이 zig-zag 형태가 될 수 밖에 없는 것이다. 이런 이유로 학습이 비효율적이게 되고 오래 걸리게 되는 것이다.

  • exp 연산 : 시그모이드는 식 s(z)=11+e−zs(z)= \frac 1{1+e^{-z}} 에서 확인할 수 있듯, exp 연산을 포함하고 있다. 해당 연산은 비용이 많이 든다(=시간이 오래 걸린다).


tanh(하이퍼볼릭 탄젠트)

그림 출처 - Stanford univ. CS231n

그림으로 알 수 있듯이 시그모이드 함수와 굉장히 유사하게 생겼다. 다만, 0이 중심에 있는 것으로 보아 zero-centered 문제는 해결됨을 알 수 있다.

tanh(x)=ex−e−xex+e−xtanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}

그리고 여전히 exp 연산을 포함한다. 따라서, 가지는 단점은 다음과 같다.

  • Saturation : 시그모이드와 비교하면 조금 나아졌지만, 여전히 문제가 있다.
  • exp 연산

역시 시그모이드와 비슷한 이유로 현재는 잘 사용하지 않는다.


ReLU

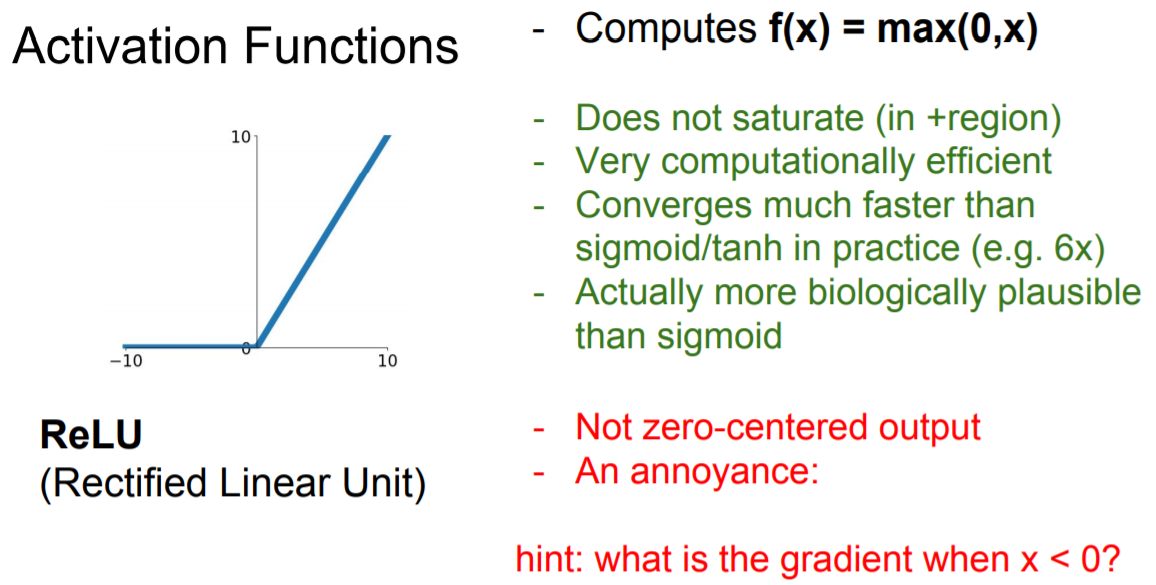
그림 출처 - Stanford univ. CS231n

ReLU 함수는 음수에서는 모두 0으로 양수에서는 그 값 그대로 처리한다. 따라서 함수의 식f(x)=max(0,x)f(x) = max(0,x) 또한 매우 직관적이다. 이처럼 단순하지만 잘 동작하므로 최근에도 많이 쓰이고 있다.
ReLU 함수가 가지는 장점은 다음과 같다.

  • 수렴 속도: 그래프로 알 수 있듯이 양수의 영역에서는 Saturated 하지 않으므로 수렴속도가 매우 빠르다. AlexNet 논문에서도 확인할 수 있듯이 tanhtanh 보다 6배나 바르다.
  • exp 연산 x : 기존 활성화 함수들은 exp 연산에 의해 미분 계산 비용이 들었지만, ReLU는 미분이 0 아니면 1 이므로 연산에 별다른 비용이 들지 않는다.

물론 단점도 존재하기는 한다.

  • Not zero-centered
  • 음수 영역에서 Saturation : 그래프에서 볼 수 있듯이 음수 영역에서는 기울기가 0이다(=미분값이 0). 이로 인해 활성화 함수의 입력으로 음수를 준다면 뉴런이 사실상 죽어버린다(=더 이상 값이 업데이트 되지 않음).
  • Dead-ReLU : 첫째로 초기화를 잘못한 경우, 가중치 평면이 Data cloud 에서 멀리 떨어진 형태를 가지게 된다. 이런 경우에는 어떤 입력 데이터에서도 활성화가 되지 않는다.
    둘째는 좀 더 흔한 경우로 Learning rate가 높으면 Data cloud를 벗어나게 되어서 역시 업데이트가 진행되지 않는다. 이런 경우, 학습이 잘 진행되다가 어느 순간 죽어버린다(수렴되지 않고 이상한 값을 마구 뱉음).

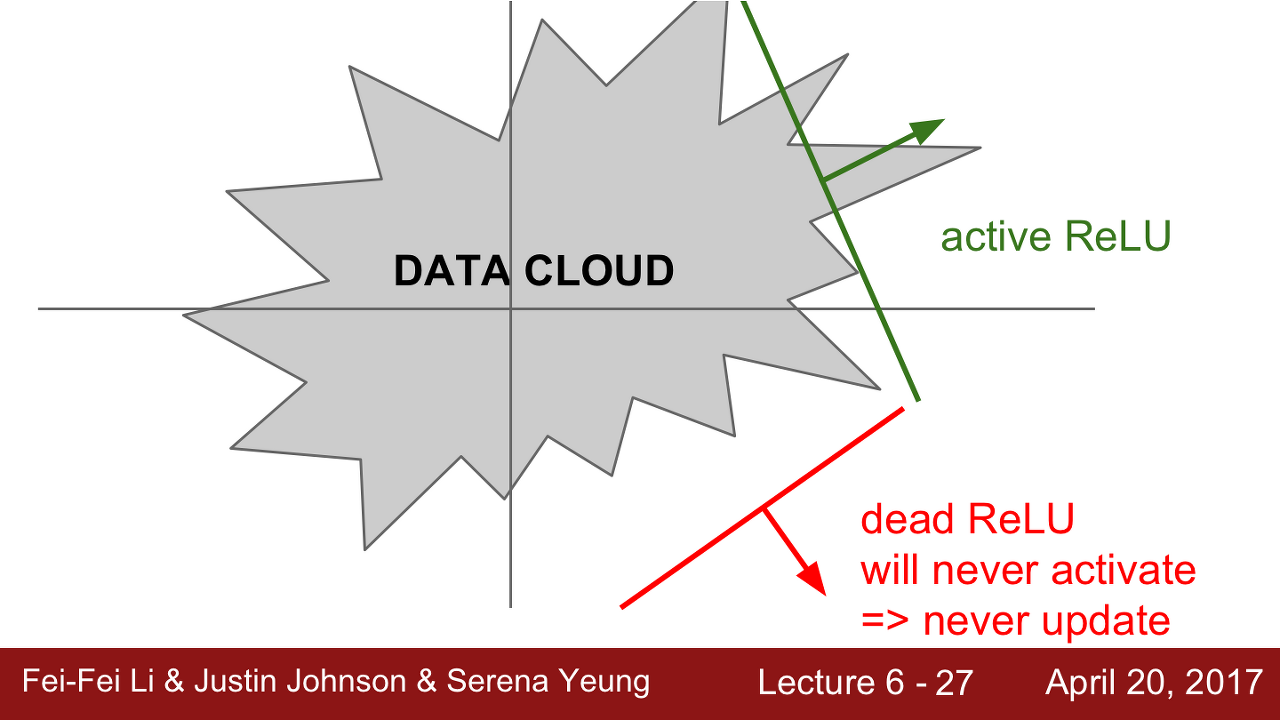
    그림 출처 - Stanford univ. CS231n



이 외에도 ReLU에서 더 발전한 형태인 Leaky ReLU, PReLU, ELU 등이 있다. 하지만 본 글에서는 이 정도 범위만 다루도록 하겠다. 다음 포스팅에서는 LRN(Local Response Normalization)을 다뤄볼 예정이다.

profile
SAsgaNAmabeer
이전 포스트

[AI] AlexNet (1) 논문 읽기

0개의 댓글