Graph , Tree, Binary

Graph

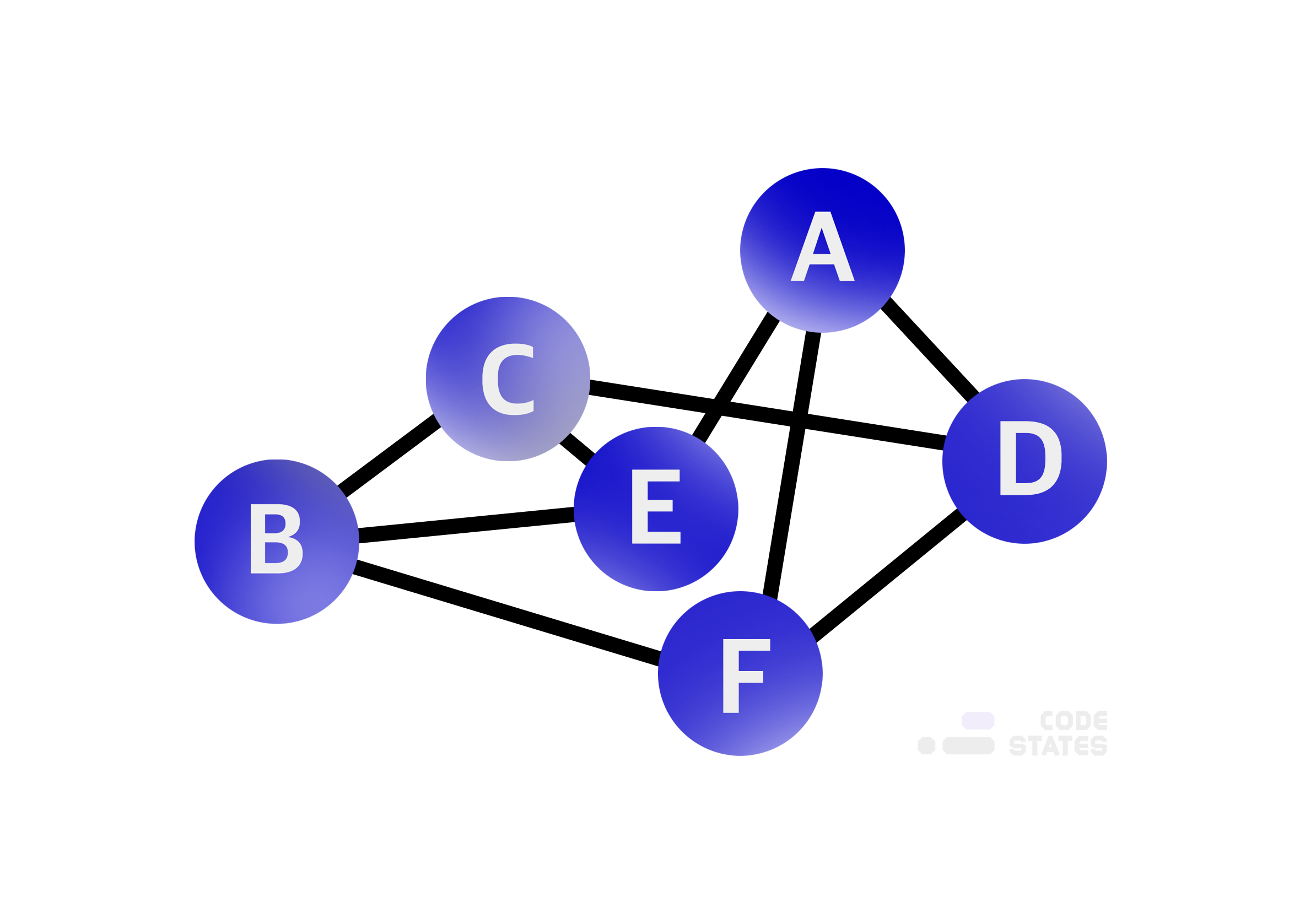
수학에서 보던 그래픽와는 다르게, 컴퓨터 공학에서는 거미줄 처럼 여러개의 점들이 선으로 이어져 있는 복잡한 네트워크 망같은 모습임. '여러개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조

출처: 코드스테이츠

Vertex(정점)은 점, edge(간선)은 이러한 점들을 직접적으로 이어주는 선을 의미. edge로 연결되어 있지 않더라도 다른 점을 통해 간접적으로 연결될 수 있음. 포털 사이트의 검색 엔진, SNS, navigation에서 사용하는 자료 구조.

let relation = {
sasha: {
	lisa: true;
	coco: true;
},
lisa: {
	sasha: true;
	coco: true;
}
coco: { 
	sasha: true;
	lisa: true;
}
}
consol.log(relation.sasha.lisa); // true
console.log(relation.lisa.coco); // true

하지만, 상기의 예는 관계가 있는지 유무만 파악할 수 있을뿐, 관계가 어느정도인지는 알 수가 없음. 이를 비가중치 그래프라고 부름. 가중치 그래프로 바꿔준다면, 더 자세한 정보를 담을 수 있음.

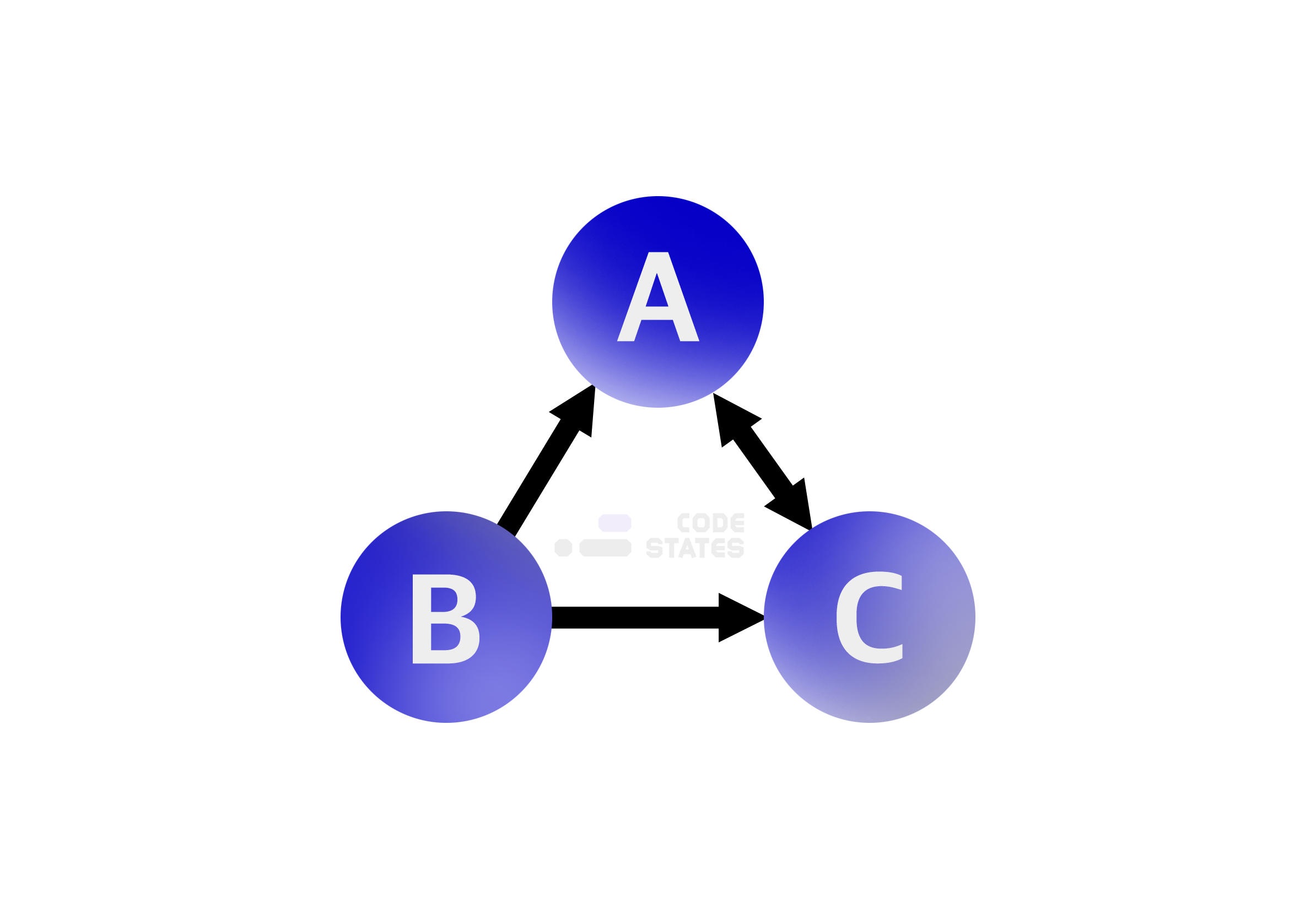
• undirected graph(무향그래프): 간선의 방향이 따로 정해져 있지 않은 그래프. directed 로 구현된다면 쌍방향이 아닌 단방향으로만 흐름을 나타낼 수 있음.
• in-degree(진입차수) / out-degree(진출차수) : 한 점에 집입하고 진출하는 간선이 몇 개인지 나타냄.
• adjacency(인접): 간선이 직접적으로 이어져 있는 상태
• self loop (자기 루프): 정점에서 진출하는 간선이 다른 정점을 거치지 않고, 곧바로 자기 자신에게 진입하는 경우
• cycle: 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있는 경우

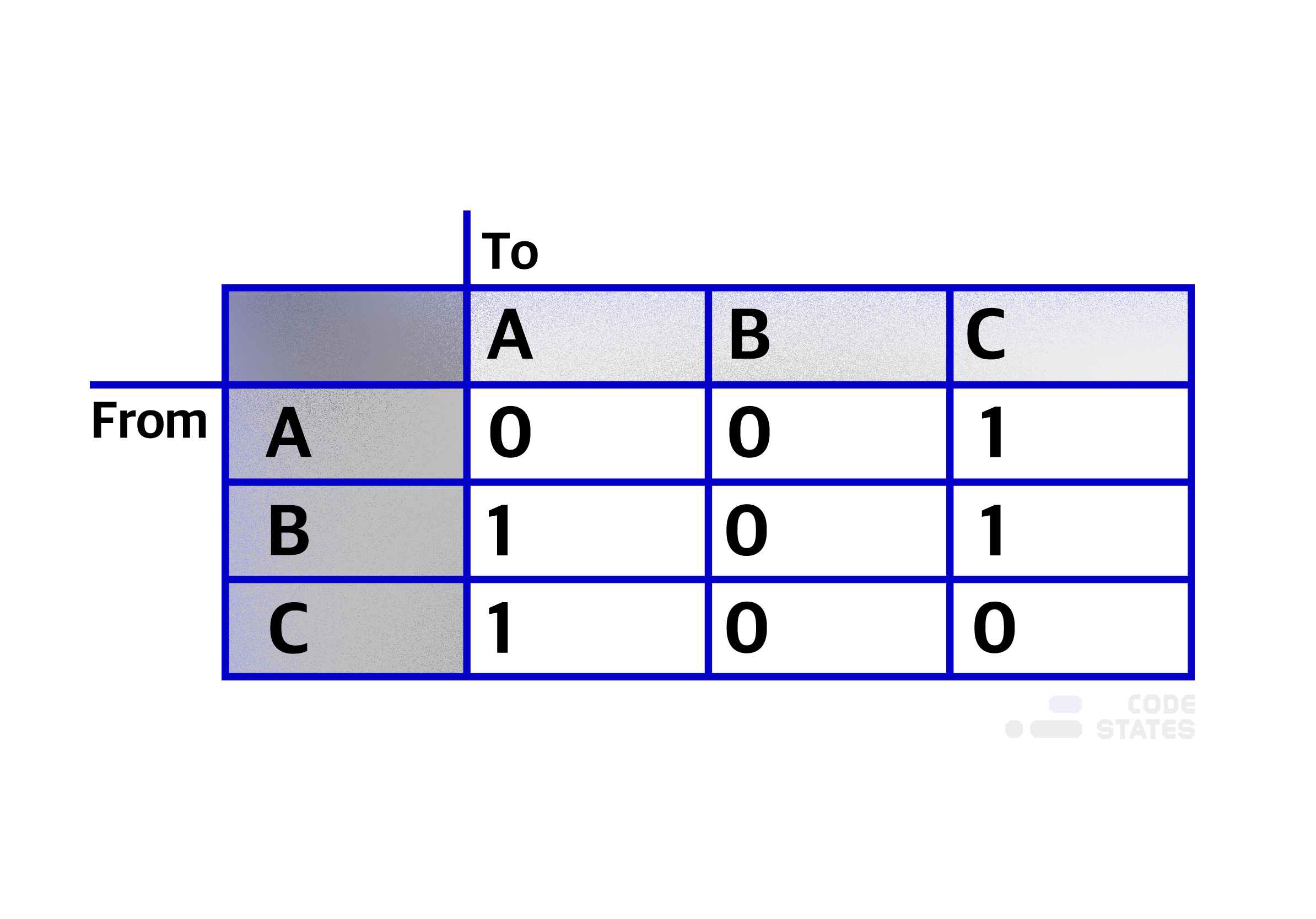
인접 행렬

인접 행렬은 정점들간의 인접함을 표시해 주는 행렬로 2차원 배열의 모습을 하고 있음. 하기 그래프는 각 정점 간 진입과 진출을 보여주고 있음. 네비게이션에서 주로 가장 빠른 경로를 찾고자 할 때 주로 사용.

출처: 코드스테이츠

인접 행렬로 나타내면 하기와 같음.

출처: 코드스테이츠

• A -> C [0][2] === 1
• B -> A, B -> C [1][0] === 1, [1,2] === 1
• C -> A [2][0] ===

인접 리스트

각 정점이 어떤 정점과 인접한지 리스트의 형태로 볼 수 있는 표현 방식. 각 정점마다 하나의 리스트를 갖고 있으며(행), 이 리스트에는 자신과 인접한 다른 정점들이 담겨져 있음.

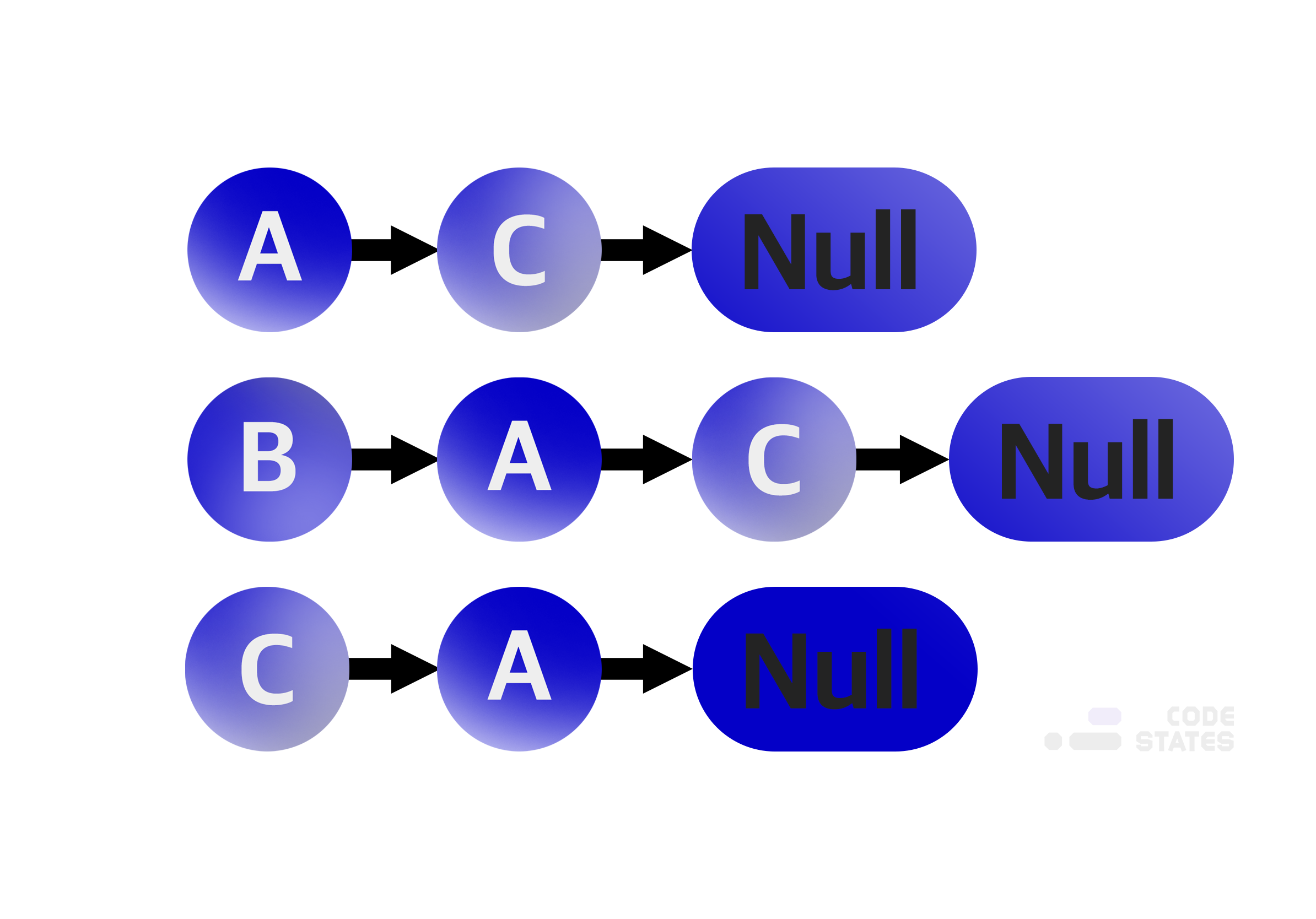
출처: 코드스테이츠

B의 경우, A와 C로 이어지는 두 개의 진출로를 갖고 있음. 하지만 인접 리스트에서는 A를 먼저 써줬는데, 순서는 사실 중요하지 않음. 대신 우선순위를 주고 싶다면 먼저 써주면 됨. 우선 순위가 중요하다면 queue 나 heap 같은 다른 자료 구조를 사용하는 것이 더 적합함.

인접행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 메모리를 많이 차지하게 됨. 따라서 메모리를 효율적으로 사용하고 싶다면 인접 리스트를 사용.

Tree

데이터가 바로 아래에 있는 하나 이상의 데이터에 단방향으로 연결되는 계층적 자료 구조. 데이터를 순차적으로 나열시킨 형태의 선형(linear) 구조가 아니라 하나의 데이터 뒤에 여러개의 데이터가 존재할 수 있는 비선형(Nonlinear) 구조로 되어 있고, 아래로만 뻗기 때문에 cycle이 없음. 주로 컴퓨터 디렉토리 혹은 dom 내 tree 구조를 대표적인 예로 들 수 있음.

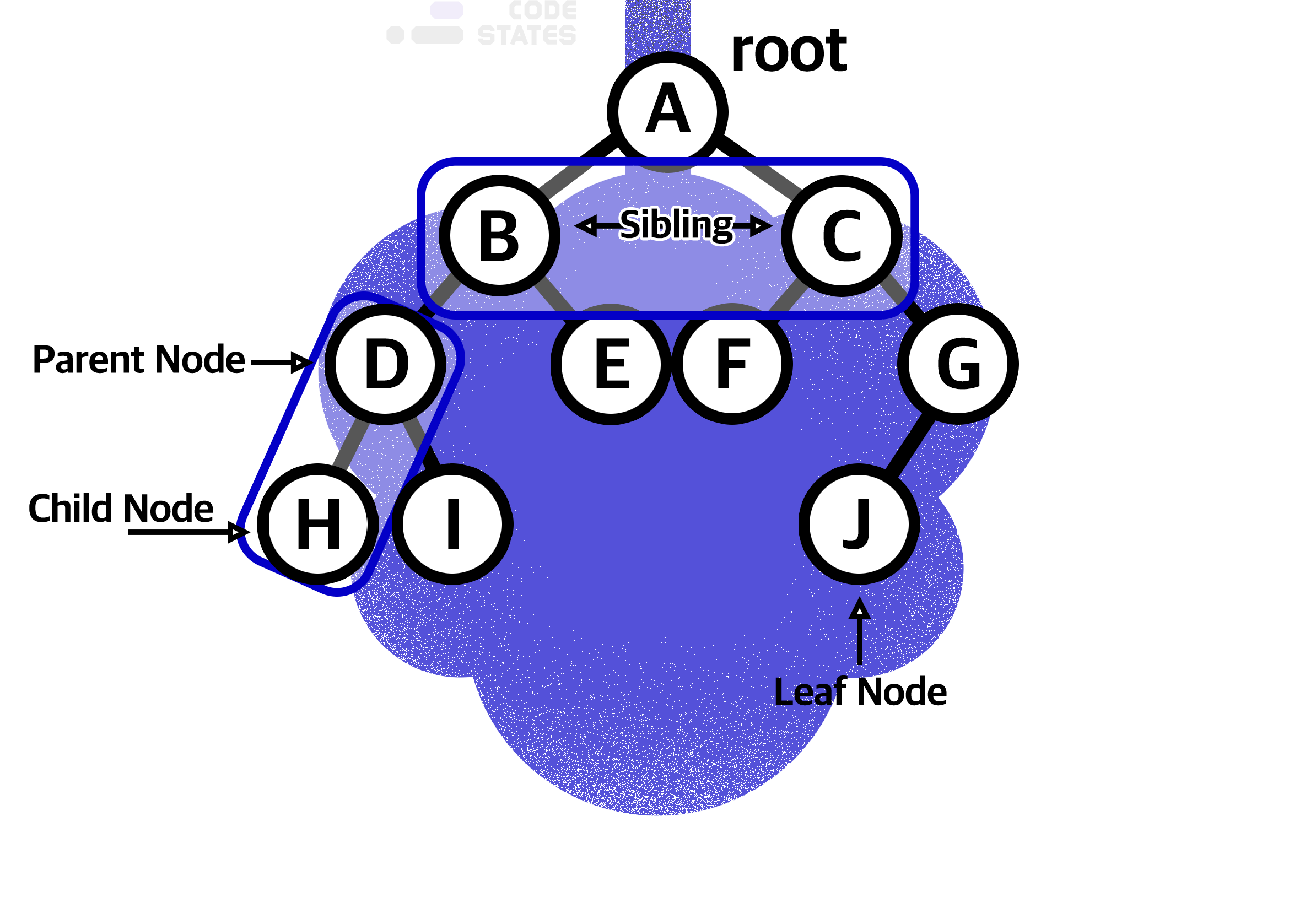
출처: 코드스테이츠

Root라는 첫 데이터를 시작으로 여러 개의 데이터를 edge로 연결. 데이터를 node라고 하며, 연결되며 부모/자식 관계를 갖게 됨. 자식이 없는 node는 나뭇잎과 비슷하다고 하여 leaf node라고 부름.

출처: 코드스테이츠

• level: 노드 간 간격을 뜻함. 첫 파일인 root는 레벨1로 설정
• Height: root부터 가장 안쪽 node까지의 level
• depth: 특정 node부터 root까지의 level
• Sub tree: 내부에 tree의 모양새를 갖춘 작은 tree를 이루는 말.

Binary tree

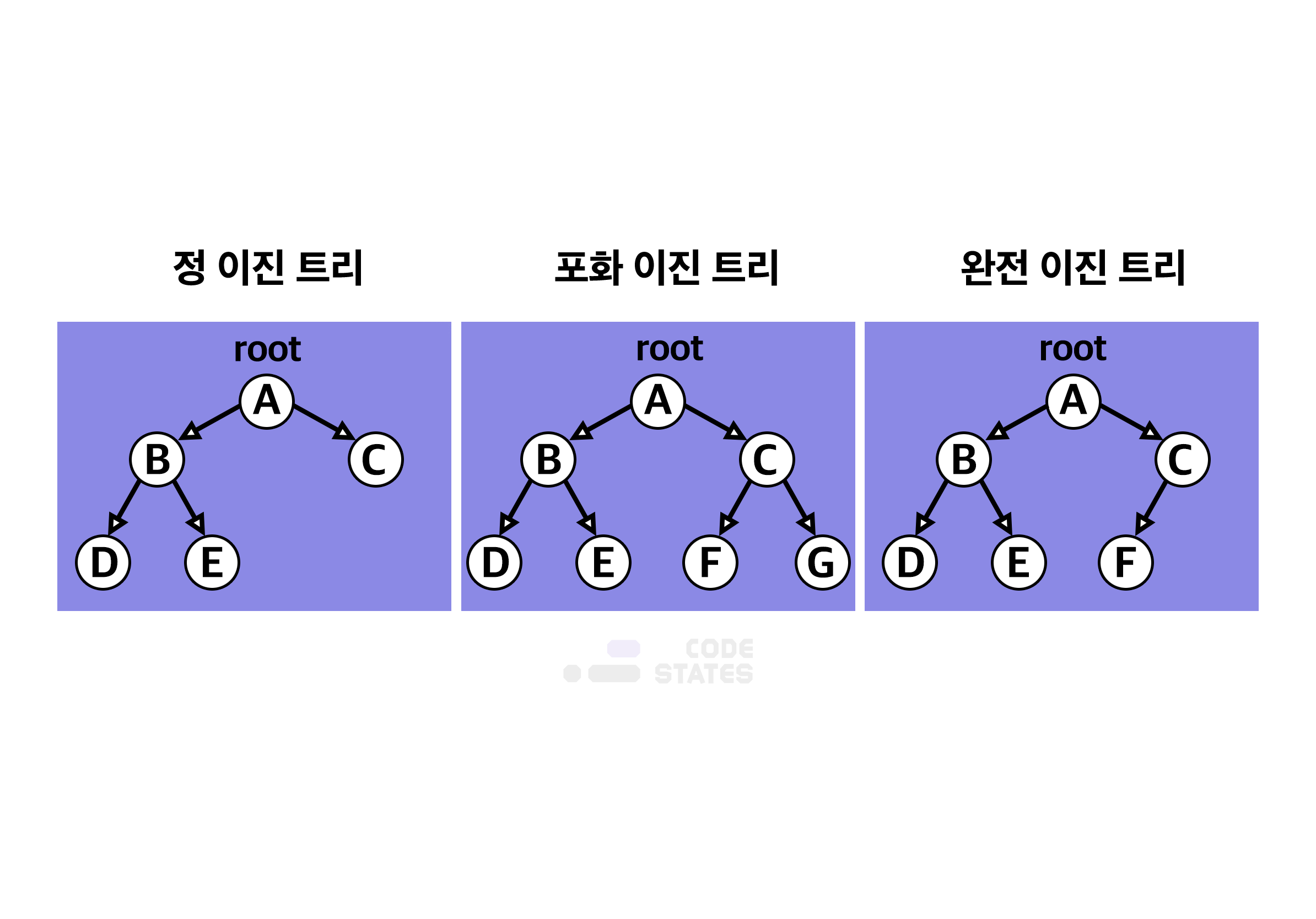
최대 두 개의 자식 node들로 구성된 tree. 왼쪽 자식과 오른쪽 자식으로 분류. 이진 트리는 자료의 삽입, 삭제 방법에 따라 하기와 같이 3가지 type으로 나눠짐.

• Full binary tree (정 이진 트리): 0 or 2개의 자식 node를 지님.

• Complete binary tree (완전 이진 트리): 마지막 level을 제외한 모든 node가 가득 차 있어야 하고, 마지막 레벨의 node는 최소 왼쪽 자식 node가 채워져 있어야 함.

• Perfect binary tree (포화 이진 트리): 정 이진 + 완전 이진 트리, 모든 노드가 다 채워져 있는 tree.

• binary search tree: 모든 왼쪽 자식 node들은 루트나 부모보다 작은 값이고, 모든 오른쪽 자식 node는 루트나 부모보다 큰 값을 가지고 있는 특징을 지닌 tree.