[알고리즘] 다익스트라 알고리즘(최단거리 알고리즘)

최단 경로 알고리즘

• 가장 짧은 경로를 찾는 알고리즘을 의미한다.
• 문제상황
  • 한 지점에서 다른 한 지점까지의 최단 경로
  • 한 지점에서 다른 모든 지점까지의 최단 경로
  • 모든 지점에서 다른 모든 지점까지의 최단 경로
• 각 지점은 그래프에서 노드로 표현
• 지점 간 연결된 도로는 그래프에서 간선으로 표현

다익스트라 최단 경로 알고리즘

• 특정한 출발 노드에서 출발하여 다른 모든 노드로 가는 최단 경로를 계산한다.

• 음의 간선이 없을 때 정상적으로 동작한다. (=현실 세계의 도로)

• 그리디 알고리즘으로 분류된다. 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정을 반복하기 때문이다.

• 동작과정
  
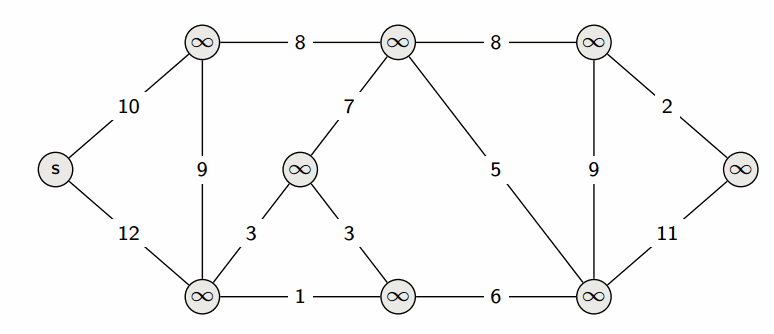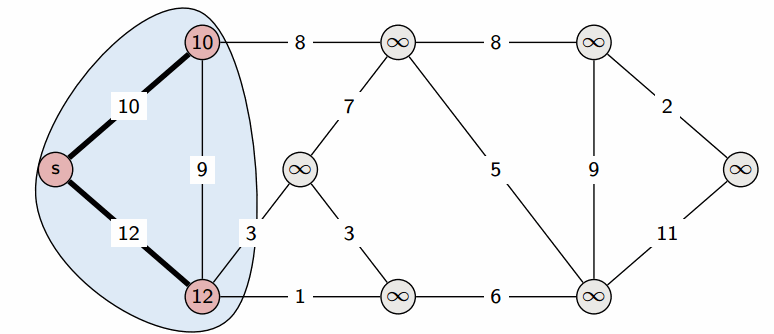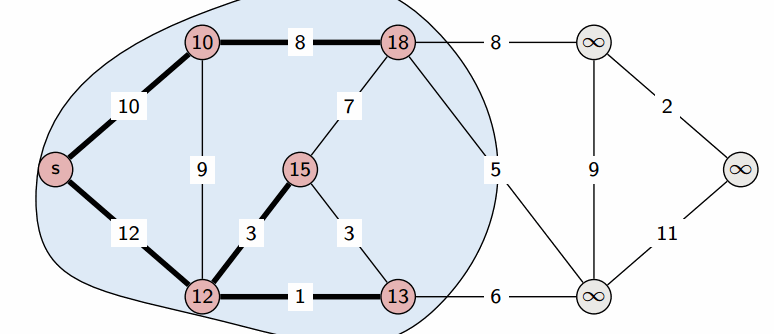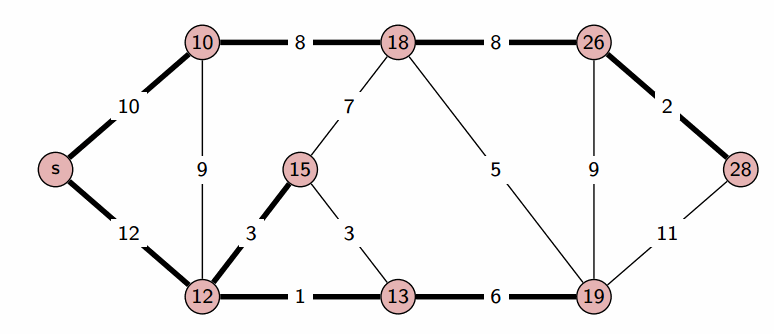
  1️⃣ - 출발 노드를 설정한다.
  2️⃣ - 최단 거리 테이블을 초기화한다. (간선길이를 모두 무한으로 정의)
  3️⃣ - 방문하지 않은 노드 중에서 가장 거리가 짧은 노드를 선택한다.
  4️⃣ - 해당 노드를 거쳐가는 경우과 거쳐가지 않은 경우를 비교하여 최단거리 갱신한다.
  5️⃣ - 3️⃣, 4️⃣ 과정을 반복한다.

• 간단한 구현 O(n²)
  단계마다 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하기 위해 매 단계마다 1차원 테이블의 모든 원소를 확인(순차 탐색)한다.

  n, m = map(int, input().split())
  INF = int(1e9)
  
  canSee = list(map(int, input().split()))
  
  graph = [[] for _ in range(n)]
  visited = [False] * (n)
  distance = [INF] * (n)
  
  for _ in range(m):
    a, b, t = map(int, input().split())
      graph[a].append((b, t))
  
  def get_smallest_node():
    min_value = INF
    index = 0
    for i in range(n):
      if distance[i] < min_value and not visited[i]:
        min_value = distance[i]
        index = i 
    return index
  
  def dijkstra(start):
    distance[start] = 0
    visited[start] = True
    for v in graph[start]:
      distance[v[0]] = v[1]
  
    for _ in range(n - 1):
      now = get_smallest_node()
      visited[now] = True
      for j in graph[now]:
        cost = distance[now] + j[1]
        if cost < distance[j[0]]:
          distance[j[0]] = cost
  
  dijkstra(0) # 시작노드 0
  
  print(distance[-1]) # 종료노드 n-1

• 힙 자료구조로 구현 O(nlogn)
  단계마다 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하기 위해 힙 자료구조를 이용한다.

  import heapq
  n, m = map(int, input().split())
  INF = int(1e9)
  
  graph = [[] for _ in range(n)]
  distance = [INF] * (n)
  
  for _ in range(m):
    a, b, t = map(int, input().split())
      graph[a].append((b, t))
  
  def dijkstra(start):
    q = []
    heapq.heappush(q, (0, start))
    distance[start] = 0
    while q:
      dist, now = heapq.heappop(q)
      if distance[now] < dist:
        continue
      for i in graph[now]:
        cost = dist + i[1]
        if cost < distance[i[0]]:
          distance[i[0]] = cost
          heapq.heappush(q, (cost, i[0]))
  
  dijkstra(0)
  
  if distance[-1] == INF:
    print(-1)
  else:
    print(distance[-1])

참고 링크
https://haningya.tistory.com/116
https://www.youtube.com/watch?v=acqm9mM1P6o