[알고리즘] 너비우선탐색 응용

한수찬·2024년 8월 24일

알고리즘

bfs의 정답을 정리한다기보단, 제가 해결하는 과정에서 깨달은 부분들을 기록하는 것에 중점을 두었습니다.

기본 - 격자형그래프

큐를 사용하는 이유, 왜 '너비우선'인지 등 기본적 개념은 다른 블로그에 잘 정리되어있으니 제가 생각하는 포인트들만 정리해보겠습니다

BFS는 완전탐색 알고리즘의 방법 중 하나입니다. 모든 경우(루트)를 탐색하는 것입니다.

모든 경우를 탐색하겠다는 확신이 코딩테스트 상황에서 중요합니다. 모든 경우를 봐야지만 예외없이 풀린다라는 확신이 있어야 이상한데서 시간줄일라고 신경쓰지 않고 쭉 밀고 나갈 수 있습니다.

그러다 보니 웬만한 bfs 문제들이 dfs로도 풀리겠죠? 데이터를 보는 순서만 틀리지, 마찬가지로 모든 루트를 보게 되는 완전탐색이니까요

완전탐색의 방법은 많이 있습니다. 격자형 그래프의 경우 직관적으로 bfs가 적합하기때문에 웬만하면 일단은 bfs를 사용하게 됩니다. (일단해본다라는 사고도 중요한게, 안풀릴경우 다른 알고리즘의 가능성으로 빠르게 전환할 수 있기 때문)

최단경로 보장 탐색

출발지와 시간, 거리 라는 개념이 들어갔을 때 어떤 목적지이든 최단경로임을 반환하게 보장합니다.
단 시간, 거리라는 개념을 큐에 넣을 때 같이 관리해주어야 기록이 됩니다.

기본 - 백준2178 미로탐색

https://www.acmicpc.net/problem/2178
격자형 그래프에 출발지도, 목적지도 정해주는 기본적인 bfs 알고리즘 문제입니다.
왼쪽 위에서 오른 쪽아래까지 탐색하는 문제이며, 목적지에 도착하지 못하는 경우 또한 생각하지 않아도 됩니다.

문제의 정답은 목적지까지 걸리는 시간을 출력하는 것입니다.
시간이라는 정보를 bfs로 탐색하는 동안 어떻게 관리해나갈지에 따라 풀이가 달라집니다.

1. 큐에 들어오고 나가는 정보로 관리

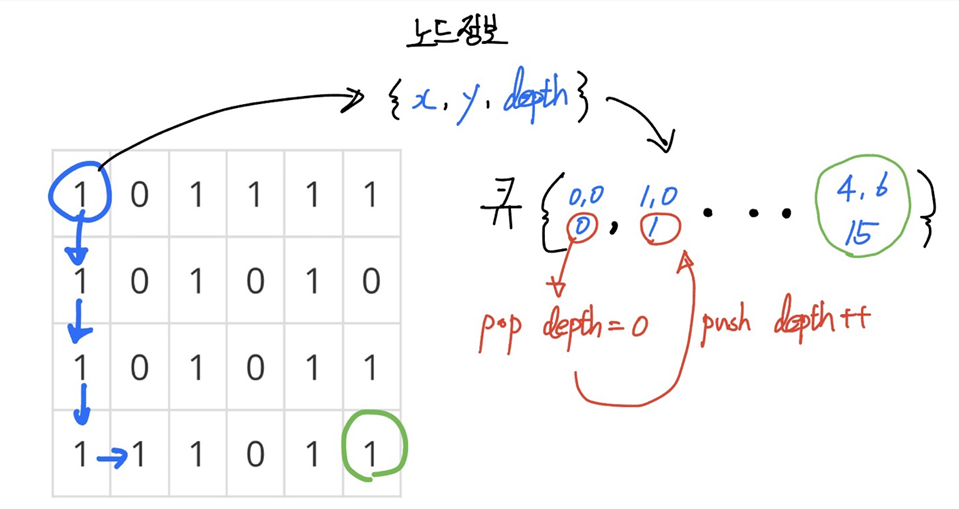
탐색할때는 큐에 격자형 그래프의 x,y값만 넣어서 그래프의 어디를 탐색했는지만 필요하지만
x,y값에 추가로 지금 푸쉬될 그 노드가 몇번째로 탐색한 노드인지에 대한 정보도 추가해서
팝되는 노드기준으로 인접노드가 푸쉬되기때문에 팝되는 노드의 depth+1의 값으로 새로 푸쉬하는 원리입니다.

2. 그래프에 뿌려진 정보 관리

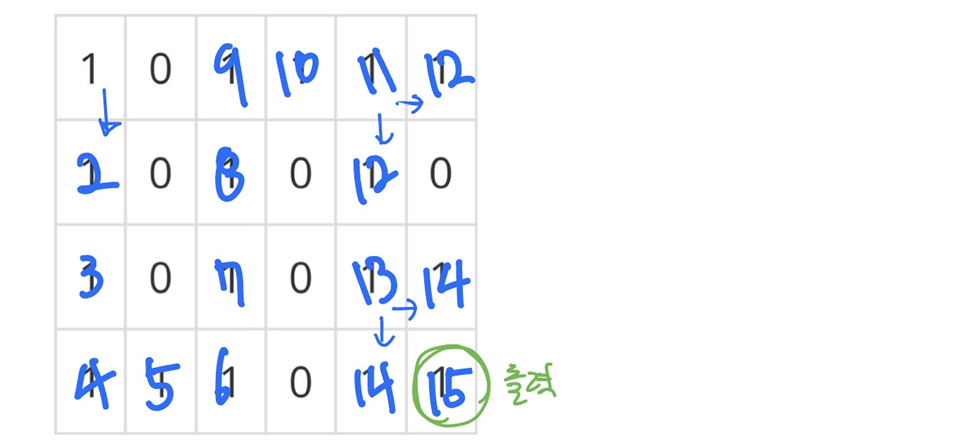
첫번째 방법에서도 이미 방문했던 노드에 방문을 다시 할 필요가 없기 때문에 그래프의 정보를 수정하거나 추가하여 방문체크를 해줍니다.
새로 visitedMiro[n][m]처럼 크기가 같은 bool형 배열을 만들던가, 방문한 노드를 벽으로 간주하게 1에서 0으로 수정해서 로직에서 알아서 걸러지게 해주는 방법 등이 있습니다.
이처럼 기존 혹은 새로운 그래프에 정보를 넣어 관리할 수 있고 이문제의 depth또한 그렇게 관리할 수 있습니다.
결국 목적지에 도달하는게 확정되어있으니 bfs를 돌리면서 방문하는 노드를 이전에 방문한 노드의 값 + 1 로 수정한 후 최종적으로 목적지 노드의 값을 출력하는 방법입니다.

응용1 - 그래프 관리

위 미로찾기 같은 문제는 조건이 단순하여 이미 주어진 그래프의 값을 수정해가며 정보를 관리했습니다.

대신에 3차원배열로 같은 크기의 배열을 만들어 내어 그 x,y위치에 해당하는 노드 정보들을 나누어 관리할 수 있습니다. ex) [n][m][3]

여러개로 나누어 관리할수록 더욱 직관적이고 편리하게 문제를 해결해나갈 수 있습니다.

응용1 - 백준14442 벽부수고이동하기2

https://www.acmicpc.net/problem/14442

아래 그림은 우하상좌 순서로 탐색한다고 했을 때, 각 배열의 초기상태와 중간상태입니다.

각 노드를 탐색하여 큐에 푸쉬할지를 정할때 [0]에서 벽인지, [1]에서 방문했는지, [2]에서 이전에 방문했다면 벽을 몇번부수고 방문했는지 등을 확인해서 푸쉬시킬 수 있습니다.
이 문제의 포인트는 완전탐색을 유지한다는 점입니다. 이미 방문했더라도 벽을 덜 부수고 또 방문할 수 있다면 추후에 어떻게 달라질지 모르기 때문에 덜부순상태로 한번더 푸쉬하고 [2]를 최신화해줍니다.
그림 오른쪽 아래를 보면 2번부수고 [1][2]노드를 방문한 경우와 1번 부수고 방문한 경우 모두 큐에 들어가서 가능성을 검토하고 있죠.
여기서는 시간정보를 큐에 넣어서 구하고 있지만, 시간정보 또한 3차원배열 인덱스를 하나 더 파서 관리하는 풀이도 있을 수 있습니다.

응용2 - 큐 안 노드관리

노드가 큐에서 pop되는 순간 얻어야하는 정보나 처리가 중요하거나,

(아직 그런문제를 본적은 없지만) bfs 탐색 중간에 중단하고 그 시점에 큐에 들어가 있는 노드들의 정보가 필요한 상황에서

큐안 노드관리를 해주어야 할 것입니다.

앞서 최단경로, 시간관리할때 편리하게 활용됩니다.

///적절한 문제 찾으면 여기 추가///

응용3 - 탐색루트

격자형 그래프에 집중하다보면 관점이 고착되는 경향이 있더라구요.

결국 탐색 순서, 범위는 자유롭게 지정해줄 수 있습니다. 그러한 노하우를 응용3문제들에서 익혀야, 그래프가 안주어진 응용4문제들에서도 bfs를 써먹을 수 있게되는것같습니다.

응용3 - 백준7569 토마토

https://www.acmicpc.net/problem/7569

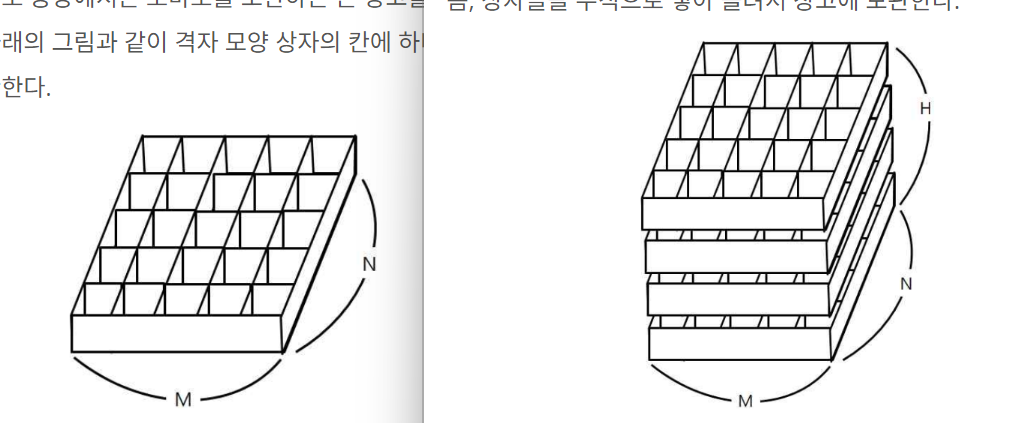
백준에는 토마토 문제가 두개인데 위처럼 하나는 격자형으로 주어지고 하나는 입체적인 격자형그래프로 주어집니다. 탐색하는 방향이 상하좌우에서 위아래까지 추가되고 로직은 그대로입니다.
bfs 로직이 꽤 긴편인데 부분부분을 나누어 생각하고 활용해야합니다.
탐색루트와 중간 로직에 해당하는 부분입니다. 그부분만 갈아끼우면 된다는 것을 이해합시다.

int dx[] = {0,0,1,-1};
int dy[] = {-1,1,0,0};

////

int dx[] = {0,0,1,-1,0,0};
int dy[] = {-1,1,0,0,0,0};
int dz[] = {0,0,0,0,1,-1};

응용3 - 백준1600 말이되고픈원숭이

https://www.acmicpc.net/problem/1600

상하좌우로만 움직일 수 밖에 없는 원숭이가 주어진 수만큼은 체스판의 말처럼 이동할 수 있는 문제입니다.
그래프를 3차원배열로 분리하여 그래프에 정보를 뿌려서 완전탐색으로 푸는 방식이고, 벽부수고이동하기와 거의 유사한 문제입니다.
토마토도 그렇고 이문제도그렇고 각각 백준난이도로 골드5, 골드3으로 탐색루트를 건들지 않은 자매문제들과 난이도가 같습니다.
결국 탐색루트응용은 알고리즘 난이도 자체에 큰영향을 못주지만, 자유로운 관점을 가져서 탐색루트 로직을 쉽게 갈아끼울 수 있다는걸 언제나 생각하고는 있어야 이러한 문제든, 응용을 더 숨겨둔 문제든 쉽게 풀 수 있을것 같습니다.

응용4 - !격자형그래프

여태까지 본 문제들은 대놓고 격자형 그래프가 주어져서 자연스레 bfs를 떠올릴 수 있었습니다.

주어진 데이터들을 정제하고 정렬해서 그래프로 생각해야할수도, 그래프를 직접 만들어야 할 수도, 격자형그래프가 아닌경우, 아예 그래프문제가 아닌데도 너비우선탐색알고리즘을 활용하는 문제들도 있습니다.

응용4 - 백준11724 연결요소의개수

https://www.acmicpc.net/problem/11724

노드 그래프 문제

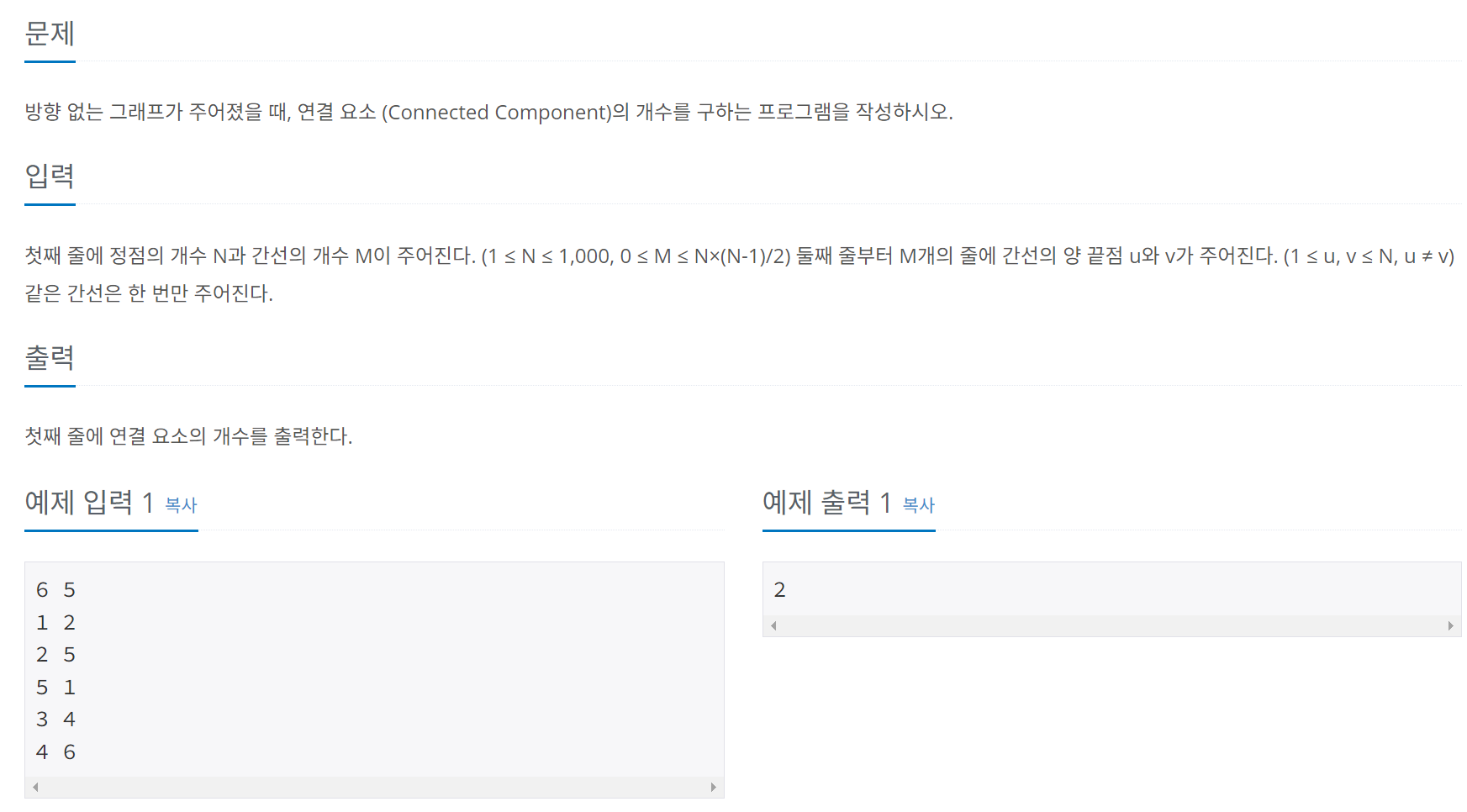
원래 bfs, dfs 알고리즘에 대한 이해는 일반적인 노드 그래프를 통해 익히는 것이 맞으나, 그 그래프를 컴퓨터 랭귀지의 자료구조로 표현하기가 번거롭기 때문에 비교적 2차원배열로 표현이 쉬운 격자형 그래프가 표준문제로 뽑히는 것입니다.
가장 일반적인 그래프 문제이고, 이 그래프는 인접행렬, 인접리스트 등으로 표현할 수 있습니다.
여태까지 그래프가 이미 주어진 bfs문제들을 풀어왔고, 탐색루트를 자유롭게 설정하는 연습을 하였습니다. 그러니 그래프를 표현하기만 하면 로직을 그대로 적용하여 풀 수 있습니다.

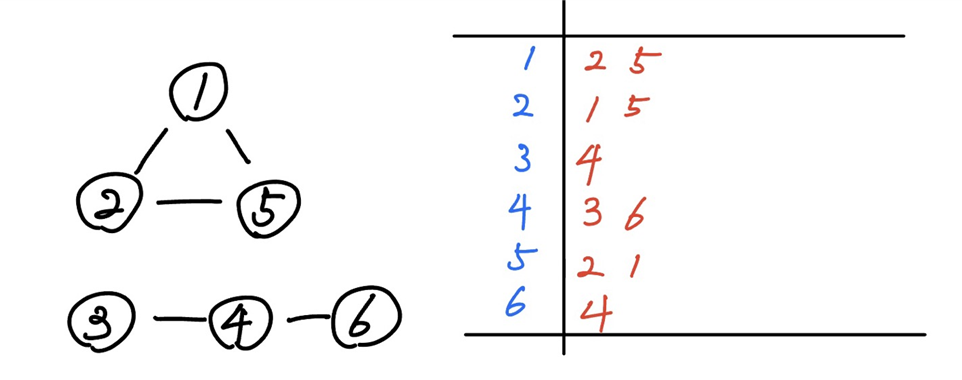
vector<vector<int>> graph(1001);
bool visited[1001];
int cnt, n, m;

void bfs(int a)
{
     queue<int> q;
     q.push(a);

     while(!q.empty())
     {
          int x = q.front();
          visited[x] = true;
          q.pop();

          for (int i = 0; i < graph[x].size(); i++)
          {
               if(visited[graph[x][i]]) continue;
               q.push(graph[x][i]);
               visited[graph[x][i]] = true;
          }
     }
     cnt++;
}

int main(void)
{
     cin >> n >> m;
     for (int i = 0; i < m; i++)
     {
          int a,b;
          cin >> a >> b;
          graph[a].push_back(b);
          graph[b].push_back(a);
     }
     
     for (int i = 1; i <= n; i++)
          if(!visited[i]) bfs(i);

     cout << cnt;
     return 0;
}

응용4 - 백준1697 숨바꼭질

https://www.acmicpc.net/problem/1697

그래프가 없지만 그래프탐색적 사고를 해야하는 문제

변하는 상황 속에서 같은 조건의 선택지들이 계속해서 주어지고 선택을 반복하여 목표값에 도달한다 => 너비우선탐색알고리즘 적용가능!!
사실 이 문제 또한 1차원 그래프라고 생각하면 그래프문제일 수 있습니다, 하지만 위와 같은 판단기준이 있어야 응용적용이 가능할 것이라 생각합니다.
방문체크에대한 개념도 유효하고, 큐에서 정보를 관리를 할 수도있습니다.
상하좌우 대신 +1,-1,*2 로의 탐색루트가 열려있다고 보는 것입니다.